Навигация
При y(t) = 1(t) и нулевых начальных условиях
2.1.2 При y(t) = 1(t) и нулевых начальных условиях
В этом случае необходимо изменить начальные условия и задать правую часть дифференциального уравнения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
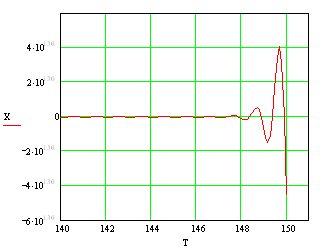
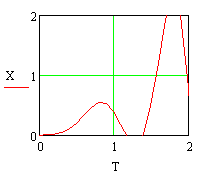
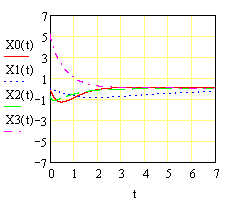
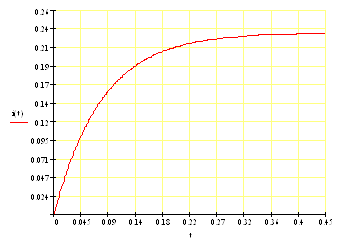
Рисунок 4. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 1(t) и нулевых начальных условиях.
2.1.3 При y(t) = 1(t) и заданных начальных условиях
Изменим условия решения дифференциального уравнения. Зададим начальные условия для искомой переменной х0(0) = 1, начальные условия для других переменных равны нулю.( x1(0) = x2(0)= x3(0) = 0).См.таблицу1.

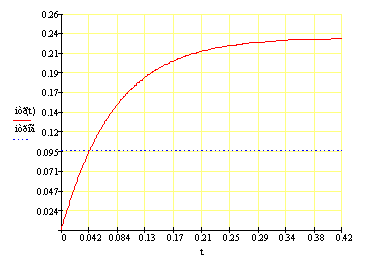
Рисунок 5. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 1(t) и ненулевых начальных условиях. х0(0) = 1
Зададим начальные условия для искомой переменной х0(0) =- 1, начальные условия для других переменных равны нулю.( x1(0) = x2(0)= x3(0) = 0).
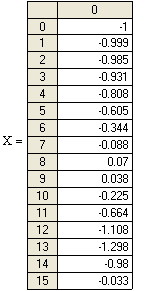

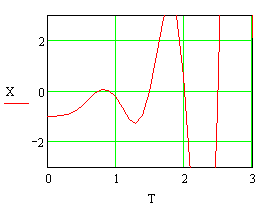
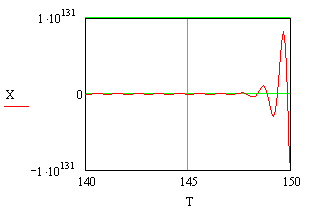
Рисунок 6. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = 1(t) и ненулевых начальных условиях х0(0) =- 1.
2.1.4 При y(t) = cos(aּπּt) и нулевых начальных условиях.
a = 0.35
|
|
|
|
|
|
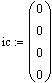
![]()
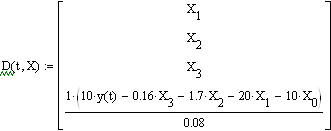
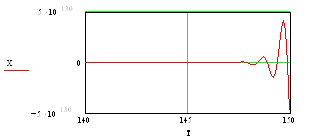
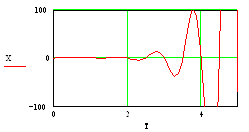
Рисунок 7. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат.
При y(t) = cos(aּπּt) и нулевых начальных условиях(a = 0.35)._
При y(t) = cos(aּπּt) и ненулевых начальных условиях.
a = 0.35
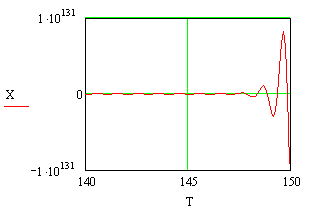
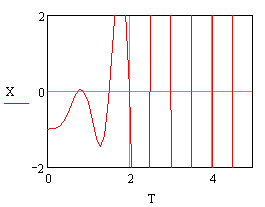
Рисунок 8. Графическое представление результатов численного решения дифференциального уравнения 4-го порядка в декартовой системе координат. При y(t) = cos(aּπּt) и нулевых начальных условиях(a = 0.35; x0(0) = -1).
Похожие работы
... мы будем определять аналитические зависимости изменения переменных состояния системы численными методами с использованием переходной матрицы, а также с помощью специальных функций MATHCAD. 2.2 Теоретическое обоснование применения преобразования Лапласа Классический метод решения системы дифференциальных уравнений высокого порядка связан с большими вычислительными затратами, особенно при ...
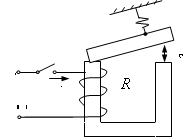
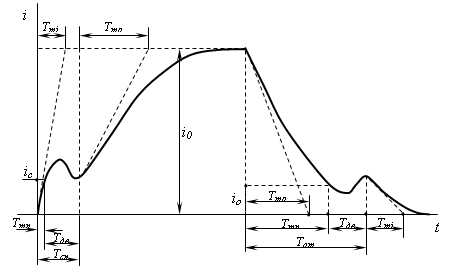
... 1. № п/п U, В R, Ом Rд, Ом L, Гн iтр, А Вариант10 220 950 950 75 0,095 Динамика срабатывания электромагнита постоянного тока. Процесс срабатывания электромагнитов имеет динамических характер. Чтобы охарактеризовать динамический режим работы электромагнита, необходимо иметь зависимость изменения тока в обмотке и пути, пройденного якорем от времени. Время срабатывания ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... , которая состоялась 22 февраля 1995 года, обсуждался ход реализации программы информатизации образования на 1994-1995 гг. Был рассмотрен вопрос о совершенствовании организации обучения информатике в общеобразовательной школе на современном этапе. Коллегия постановила признать целесообразной необходимость выделения нескольких этапов в овладении основами информатики и формировании информационной ...


0 комментариев