Навигация
Решение дифференциальных уравнений N-го порядка операторным методом
2.2. Решение дифференциальных уравнений N-го порядка операторным методом.
2.2.1 При y(t) = 0 и заданных начальных условиях (см. Табл.№1 )
К дифференциальному уравнению 4-го порядка применим преобразование Лапласа при заданных начальных условиях и у(t) = 0 и запишем его относительно изображения искомой переменной:
К линейные дифференциальным уравнениям с постоянными коэффициентами применим преобразование Лапласа, чтобы переменные вещественного аргумента t заменить на переменные комплексного аргумента S, дифференцирование заменим умножением на S, повторное дифференцирование- умножением на S^2 и т.д.
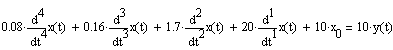
|
|
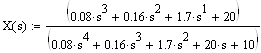
Используя обратное преобразование Лапласа, найдем оригинал искомой переменной:
![]()
![]()
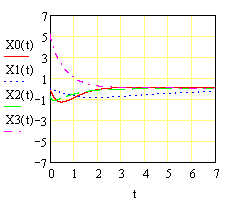
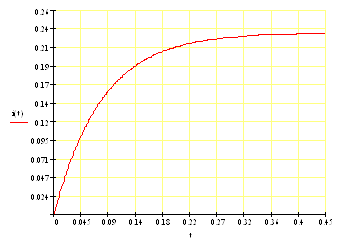
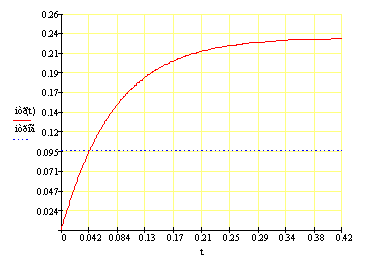
На рис. 9. показаны графики изменения переменной, полученных в результате решения заданного дифференциального уравнения путем интегрирования (кривая Х) и операторным методом (Н(t)).
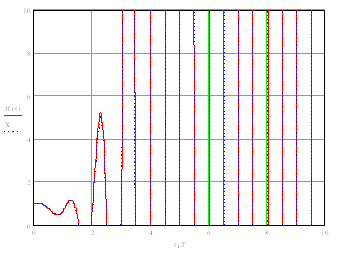
Рисунок 9. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = 0 и заданных начальных условиях.
2.2.2 При y(t) = 1(t) и нулевых начальных условиях
![]() -Изображение по Лапласу y(t) = 1(t)
-Изображение по Лапласу y(t) = 1(t)
![]()
![]()
![]()
![]()
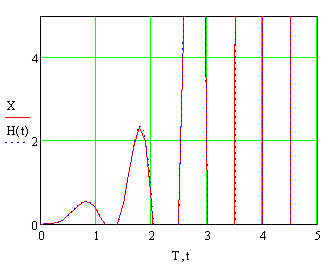
Рисунок10. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = 1(t) и нулевых начальных условиях.
2.2.3 При y(t) = 1(t) и заданных начальных условиях
![]()
![]()
![]()
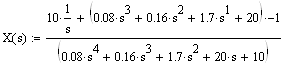
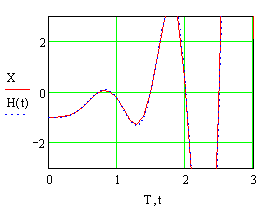
Рисунок11. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = 1(t) и заданных начальных условиях.
2.2.4 При y(t) = cos(aּπּt) и нулевых начальных условиях
![]()
![]()
![]()
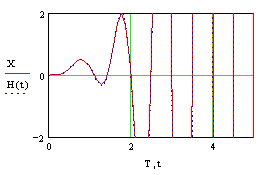
Рисунок11. Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами. При y(t) = cos(aּπּt) и нулевых начальных условиях;
3. Выводы по работе №3
В процессе данной практической работы я изучил возможности математического пакета MathCad в среде Windows для решения дифференциальных уравнений N-го порядка, используемых в инженерных расчетах электротехнических систем. Были выполнены численные методы решения дифференциальных уравнений N-го порядка. Заданное уравнение 4-го порядка описывает динамические процессы электротехнической системы. Оно было преобразовано в систему дифференциальных уравнений первого порядка (в нормальную форму Коши). Мы воспользовались функцией rkfixed(y0, t0, t1, M, D) -получили матрицу решения системы обыкновенных дифференциальных уравнений численным методом Рунге-Кута на интервале от t0 до t1 при M фиксированных шагах решения и правыми частями уравнений, записанными в D. Получено численное и графическое представление результатов.
Решение уравнения операторным методом предполагает применение преобразования Лапласа. В данной работе мы использовали преобразование Лапласа к искомой переменной системы, в частности, теорему о дифференцировании оригинала и свойство линейности преобразования Лапласа. Мы применили преобразование Лапласа (функция laplace), чтобы переменные вещественного аргумента t заменить на переменные комплексного аргумента s, дифференцирование заменить умножением на s, повторное на s в квадрате и т.д. Из полученных в комплексной области алгебраических уравнений нашли отношение выходной характеристики к входной. Это изображение обычно представляет собой передаточную функцию системы автоматического управления. Используя обратное преобразование Лапласа( функция invlaplace), найден оригинал искомой переменной.
Графики изменения искомой переменной, полученные в результате решения дифференциального уравнения двумя методами совпадают.
Похожие работы
... мы будем определять аналитические зависимости изменения переменных состояния системы численными методами с использованием переходной матрицы, а также с помощью специальных функций MATHCAD. 2.2 Теоретическое обоснование применения преобразования Лапласа Классический метод решения системы дифференциальных уравнений высокого порядка связан с большими вычислительными затратами, особенно при ...
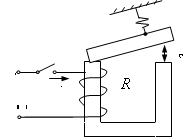
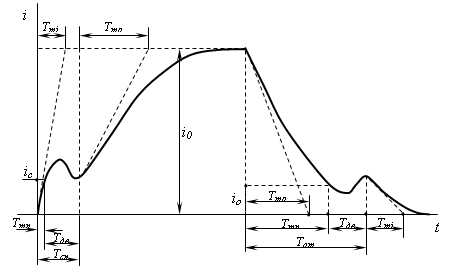
... 1. № п/п U, В R, Ом Rд, Ом L, Гн iтр, А Вариант10 220 950 950 75 0,095 Динамика срабатывания электромагнита постоянного тока. Процесс срабатывания электромагнитов имеет динамических характер. Чтобы охарактеризовать динамический режим работы электромагнита, необходимо иметь зависимость изменения тока в обмотке и пути, пройденного якорем от времени. Время срабатывания ...
... - в группе переменных, «зажатых в кулак», но этот «кулак», как мы уже отмечали, легко разжать, выводя на дисплей найденные значения с «первородной» размерностью массы (kg), длины (m) и времени (sec): пакет MathCAD «разжимает» и сам вектор, м составные размерности, приписывая к числам комбинации основных физических единиц. Но не только этим хороша размерность в задачах. Главное то , что она ...
... , которая состоялась 22 февраля 1995 года, обсуждался ход реализации программы информатизации образования на 1994-1995 гг. Был рассмотрен вопрос о совершенствовании организации обучения информатике в общеобразовательной школе на современном этапе. Коллегия постановила признать целесообразной необходимость выделения нескольких этапов в овладении основами информатики и формировании информационной ...

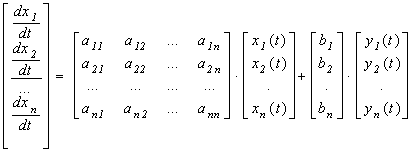
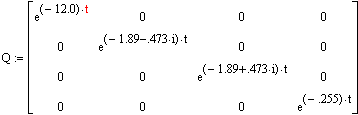

0 комментариев