Навигация
МО и ПО РФ
НГТУ
Реферат по информатике на тему «Пакет MathCAD»
факультет: АВТ
группа: А - 514
студент: Коваленко С.А.
преподаватель: Мамонова В.Г.
Новосибирск - 1997
Содержание :
Введение________________________________________________3
Возможности системы____________________________________4
2.2 Документ 1______________________________________________5
2.3 Графические возможности _______________________________6
Документ 2______________________________________________7
Документ 3______________________________________________8
Документ 4______________________________________________9
Документ 5______________________________________________10
Работа системы с файлами_______________________________11
Общение с внешними устройствами_______________________11
Система MathCAD становится более гибкой
Система MathCAD версии 3.0______________________________11
MathCAD PLUS 6.0
Решение алгебраических систем_________________________12
Великолепная семёрка MathCAD_________________________15
Сортировка___________________________________________16
Линейная аппроксимация ______________________________16
Дифференциальные уравнения_________________________17
Программирование____________________________________17
4. MathCAD или программирование на языках высокого уровня _18
1. Введение
Математические и научно - технические расчеты являются важной сферой применения персональных компьютеров . Часто они выполняются с помощью программ , написанных на языке высокого уровня, например Бейсике или Паскале. Сегодня эту работу нередко выполняет обычный пользователь ПК. Для этого он вынужден изучать языки программирования и многочисленные, подчас весьма тонкие капризные численные методы математических расчетов. Нередко при этом из под руки способного физика, химика или инженера выходят далёкие от совершенства программы.
Это не вполне нормальное положение может изменить к лучшему применение интегрированных программных систем автоматизации математических расчетов (Eureka, MathCAD, MatLab и др.). Здесь рассматриваются возможности и эволюция одной из таких систем - MathCAD.
Фирма MathSoft Inc.(США) выпустила первую версию системы в 1986 г. Главная отличительная особенность системы MathCAD заключается в её входном языке, который максимально приближён к естественному математическому языку, используемому как в трактатах по математике, так и вообще в научной литературе. В ходе работы с системой пользователь готовит так называемые документы. Они одновременно включают описания алгоритмов вычислений, программы управляющие работой систем, и результат вычислений. По внешнему виду тексты мало напоминают обычной программы .
2. Возможности системы
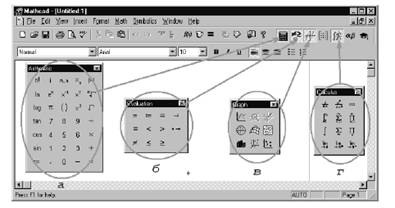
MathCAD объединяет в себе простой текстовый редактор, математический интерпретатор и графический процессор. Система ориентирована на IBM - совместимые компьютеры. Упомянутые выше документы содержат текстовые, формульные и графические блоки. На экране дисплея они занимают прямоугольные области, границы которых обычно не видны (но при введении в блок курсора противолежащие углы прямоугольных областей отмечаются прямоугольниками). Блоки выполняются слева направо и сверху вниз.
Подготовка и исполнение документов MathCAD может осуществляется с помощью: главного меню и спускающихся подменю (для их появления необходимо нажать клавишу ), командного режима (вводится нажатием клавиши и команд в верхней командной строке ), комбинации обычных клавиш, а так же с помощью управляющих клавиш. В последнем случае, например, нажатие клавиши обеспечивает вызов системы подсказок, - загрузку документов с дискового накопителя, - запись редактируемого документа на диск и т.д.
Из режимов работы необходимо особо отметить режимы auto и manual. Режим auto обеспечивает автоматические вычисления сразу после загрузки документа по мере его прокрутки (скроллинга) на экране дисплея. В этом режиме скроллинг ощутимо замедлен, особенно при использовании системы на ПК класса IBM PC XT без математического сопроцессора. Режим manual (ручной) позволяет осуществлять быстрый скроллинг без выполнения документа. Для проведения вычислений от начала документа и до конца видимой на экране дисплея его части нужно нажать клавишу .
Текстовые блоки являются не более чем комментариями. Их назначение - пояснить сухое и лаконичное математическое описание, представленное на входном языке системы. Текстовые блоки могут быть полноформатными (на всю длину строки) и в виде прямоугольников ограниченных размеров. Если ввести знак «кавычки», то на экране дисплея появится пара кавычек, между которыми вводить и редактировать текст в обычном порядке.
Текстовый редактор системы не обладает всеми возможностями специализированных редакторов текста, однако позволяет корректировать тексты, выравнивать их по краю, перемещать текстовые блоки в любое место документа и т.д. Весьма удобны средства редактирования документов, позволяющие, в частности, стирать указанный курсором блок (клавиша ) и вставлять блок на новое место (клавиша ). При необходимости можно использовать два окна системы, перенося блоки из одного окна в другое.
Математический интерпретатор системы - наиболее интересная её часть. Математические формулы, подлежащие интерпретации, записываются в общепринятом виде. Например, вычисление квадратного корня из двух в системе MathCAD задаётся как ы2 =, а не в виде PRINT SQR (2) , как это делается, скажем, на Бейсике. Для ввода формул используются шаблоны, вводимые определёнными комбинациями клавиш. Имеется возможность изменения формата представления чисел, например числа знаков после разделительной точки, погрешности вычислений и обозначения мнимой единицы (i на j и наоборот) при операциях с комплексными числами.
Чтобы вывести на экран дисплея графический блок, необходимо установить курсор на место левого верхнего будущего графика и ввести знак @. На экране дисплея появится прямоугольник - шаблон будущего графика. Начиная с версии 2.0, масштаб можно и не указывать - он вычисляется автоматически.
Возможности системы поясняют следующие конкретные примеры.
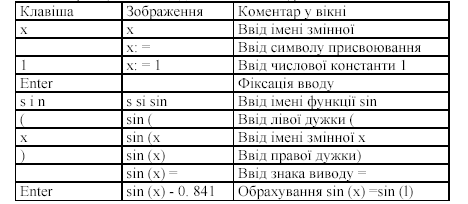
Название операции Задание операции Численный пример
2
Возведение в степень XЧY 3 = 9
Вычисление факториала X! 4! = 24
Вычисление квадратного корня \X Ц9 = 3
Вычисление абсолютного значения ЅX Ѕ-5Ѕ = 5
Сложение X+Y 2 + 3 = 5
Умножение X*Y 2Ч3 = 6
12
Деление X/Y `3 = 4
Присваивание значений переменной X:Y X : = 8
Вывод значения переменной X = X = 8
Задание циклической переменной i : = N1..N2 i : = 1,...,5
Суммирование членов ряда i \ X еX = 2i
i i
3
Перемножение членов ряда i # X Х X = 3.84Ч10
i i
1
Вычисление определённого интеграла x&f(x) у Ц2xdx = 0.93
х
0
Задание функции пользователя f(X) : ... f(x): = sin x
Инициализация переменной х : ... x : = 1, f (x) = 0.841
df(x) = 0.54
Вычисление производной x ? f (x) ` dx
Задание и проверка неравенства X > Y 5 > 4 = 1, 4 > 5 = 0
Вычисление специальных функций Jn(x) = Jn(1,.5) = 0. 242
Бесселя и интеграла вероятности J1(x) = J1(.5) = 0.242
erf(x) = erf(1) = 0.843
Документ 1. Примеры выполнения математических операций .
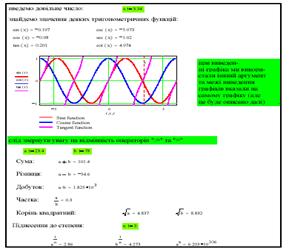
Документ 1 иллюстрирует задание и исполнение в системе MathCAD ряда математических действий. Среди них вычисление алгебраических, тригонометрических и гиперболических функций, сумм и произведений рядов, определённого интеграла и производной.
В MathCAD предусмотрены средства для решения нелинейных уравнений, не имеющих аналитических решений. Так , функция root (f(x,y,z,),x) ищет значение переменной x, при котором f(x,y,z) = 0. Более сложные вычисления (решение систем нелинейных уравнений, минимизация функций нескольких переменных и др.) обеспечиваются организацией вычислительного блока, открываемого словом Given.
Документ 2 показывает решение актуальной для садовода или любителя баньки задачи: как, сгибая железный лист, получить ящик заданного объёма. Оказывается, есть три решения. Ящик может быть неглубоким, но с дном большой площади или глубоким, но с дном малой площади. Третье решение физически нереально. Во второй части документа показано решение задачи о конструировании ящика максимального объёма, ещё более актуальной при нашем дефиците строительных материалов.
Специалистов в электротехнике и радиотехнике наверняка привлечёт способность системы MathCAD выполнять все предусмотренные в ней вычисления как с действительными, так и с комплексными числами. В документе 3 приведены примеры операций с комплексными числами, начиная от простых и кончая сложными. К последним относится вычисление комплексного кругового интеграла, в ходе которого выполняется численное интегрирование и дифференцирование с комплексными аргументами.
Начиная с версии 2.0 в MathCAD введён функционально полный набор векторных и матричных операций. Это существенно облегчает решение задач линейной алгебры. В качестве примера в документе 3 даётся решение системы линейных уравнений с комплексными коэффициентами, в ходе которого производится обращение комплексной матрицы. К таким уравнениям приводит анализ электрических и электронных цепей на переменном токе.
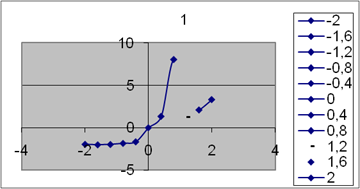
Весьма привлекательны средства линейной и сплайн-интерполяции и экстраполяции данных. Линейная интерполяция графически означает просто соединение узловых точек графика отрезками прямых. В отличии от неё сплайн-интерполяция напоминает соединение этих точек с помощью гибкой линейки. Строго математически это означает проведение через каждые три точки линии, описываемой кубическим полиномом. При этом во всех стыкуемых точках обеспечивается непрерывность как первой , так и второй производной каждого из полиномов. Сплайн-интерполяция - это мощное средство представления данных, заданных небольшим числом узловых точек.
Документ 4 демонстрирует задание в виде векторов напряжений и токов N - образной вольт - амперной характеристики туннельного диода. Затем проводиться интерполяция-экстраполяция этой характеристики описанными в документе способами . Можно заметить ,что сплайн- интерполяция в данном случае предпочтительнее линейной .
MathCAD имеет обширный набор статических операторов и функций ,обеспечивающих генерацию случайных чисел ,а также вычисление среднего ,дисперсии и вариации ,коэффициентов линейной регрессии, ряда специальных математических функций .Документ 5 организует генерацию 200 случайных чисел ,их представление на плоскости ,вычисление ряда статистических параметров и построение гистограммы распределения .
Графические возможности системы.
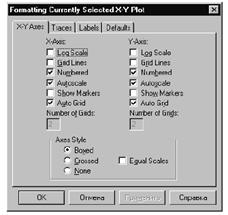
Мы уже отмечали графические возможности системы. MathCAD позволяет строить самые разнообразные графики: в декартовой и в полярной системе координат, с масштабной сеткой и без неё, с линейным и логарифмическим масштабом, с отметкой линий прямоугольниками, крестами, ромбами и т.д. Задание вида и размера графика осуществляется вводом соответствующего формата. Для задания формата можно ввести внутрь шаблона графика курсор и нажать клавишу .В верхней строке появятся данные о формате заданного графика, например:
logs = 0,0 subdivs = 1,1 size = 5,15 type = 1
Если параметры logs - нули, график строится с линейным масштабом, иначе- с логарифмическим (в этом случае параметры указывают число делений шкалы в пределах декады) . Параметры subdivs задают число делений шкалы, а параметры size - размеры графика, выраженные в знакоместах. Во всех этих случаях первый параметр относится к оси Y графика, второй - к оси Х. Параметр type описывает указание о типе графика в виде малой или большой латинской буквы. Например, указание L задаёт сплошной график, d «строит» точки в узлах и т.д. Возможна комбинация таких указаний.
Конструирование железного ящика заданного объёма
VO : = 7.5 Заданный объём ящика
W : = 4 Ширина листа
L : = 8 Длина листа
X : = 0,0.2 .. 5 Расстояние от линии
отгиба листа
V(X) : = (L - 2X)Ч(W - 2X)ЧX Объём ящика
F(X) : = V(X) -VO Основное уравнение
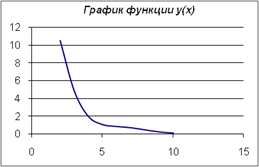
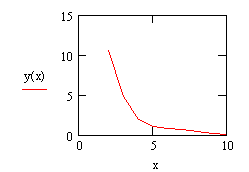
Графическое решение задачи
60
F(X), 0
20
Похожие работы
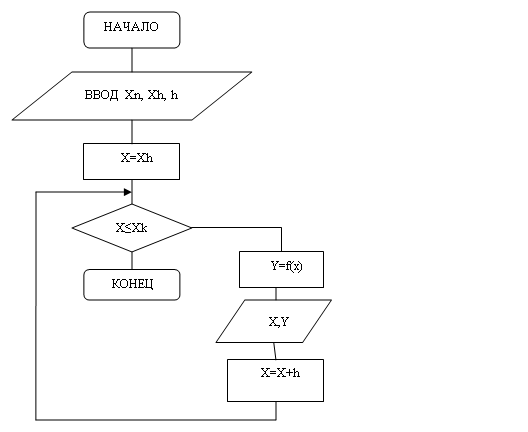
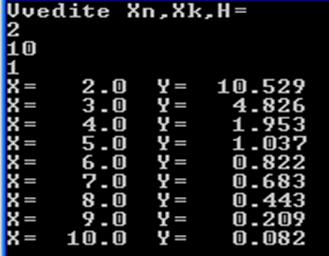
... 1,' Y=',Y: 8: 3); X: =X+H; until X>=Xk+H/2; readkey; end. Блок-схема к заданию: Результаты вычислений: Задание 1 (б) Решение программы вычисления функции с условием Решение уравнения в табличном редакторе Microsoft Excel Для реализации задачи необходимо использовать логическую функцию ЕСЛИ, которая возвращает одно значение, если заданное условие при вычислении дает ...
... іальних рівнянь у частинних похідних; - статистична обробка даних (інтерполяція, екстраполяція, апроксимація та багато іншого); - робота з векторами та матрицями (лінійна алгебра та ін.); - пошук мінімумів та максимумів функціональних залежностей; - пакет MathCAD доповнений довідником по основним математичним та фізико-хімічним формулам та константам, які можливо автоматично переносити у ...
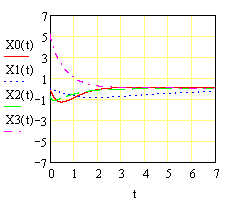
... мы будем определять аналитические зависимости изменения переменных состояния системы численными методами с использованием переходной матрицы, а также с помощью специальных функций MATHCAD. 2.2 Теоретическое обоснование применения преобразования Лапласа Классический метод решения системы дифференциальных уравнений высокого порядка связан с большими вычислительными затратами, особенно при ...
... со строками и столбцами матрицы 2.3.13 Объединение матрицы с вектором и матрицы с матрицей 2.3.14 Сортировка элементов вектора и матрицы 2.3.15 Разложение матрицы на треугольную, ортогональную 2.4 Использование матричных функций 2.4.1 Собственные значения и векторы собственных значений матрицы 2.4.2 Нахождение матрицы векторов собственных значений матрицы 2.4.3 Приведение заданной матрицы к ...


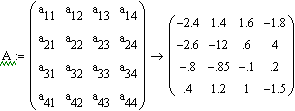
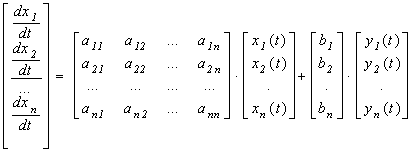
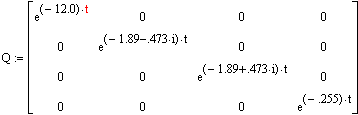
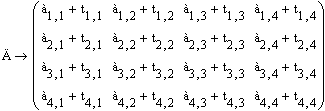
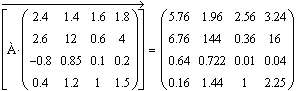

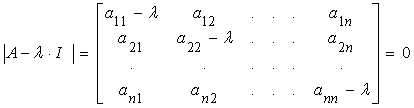
0 комментариев