Навигация
Корреляционный анализ данных
3. Корреляционный анализ данных.
На этом этапе осуществляется парное сравнение выборки результирующего показателя с выборками показателей, которые согласно теоретической модели рассматриваются как факторные, а также проверяется степень коррелируемости факторных показателей. Для этих целей строят и анализируют матрицы парных линейных коэффициентов корреляции r, которые изменяются от -1 до 1. Анализ применим лишь в случае линейной зависимости между признаками. Чем ближе значения коэффициента корреляции к -1 или к 1, тем выше степень коррелируемости соответствующих случайных величин. Однако, при r, близких к 1 или -1, регрессионные связи между соответствующими величинами устанавливаться не могут, так как эта ситуация означает фактически функциональную взаимосвязь показателей.
Значимость (существенность) линейного коэффициента корреляции проверяют на основе t-критерия Стьюдента. При этом выдвигается и проверяется нулевая гипотеза о равенстве коэффициента нулю, т.е. об отсутствии связи между х и у. Для этого определяется расчетное значение критерия:
 (1)
(1)
где r – коэффициент корреляции,
n – число наблюденеий,
σr – среднее квадратическое отклонение кэффициента корреляции.
и сопоставляется с tтабличное с заданными параметрами (уровнем значимости α, принимается обычно за 0,05, и числом степеней свободы υ = n – 2, где n – число наблюдений).
Если tрасчетное › tтабличное , то нулевая гипотеза отвергается и линейный коэффициент считается значимым, а связь между х и у – существенной, если же неравенство обратное, то связь между х и у отсутствует.
Вообще говоря, отсутствие корреляционной связи между факторным признаками и наличие тесной связи (значение парных коэффициентов корреляции 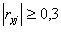 )между результативным и факторными признаками – условие включения этих факторных признаков в регрессионную модель.
)между результативным и факторными признаками – условие включения этих факторных признаков в регрессионную модель.
Кроме того, при построении модели регрессии необходимо учитывать проблему мультиколлениарности (тесной зависимости между факторными признаками), которая существенно искажает результаты исследования.
Одним из индикаторов определения наличия мультиколлинеарности между факторными признаками является превышение величины парного коэффициента корреляции 0,8 (r ≤ 0,8).
|
| сырье,м погонный | затраты на заработную плату,т.руб. | материальные затраты, тыс.руб | амортизация, тыс.руб. | полная себесто- имость, тыс.руб |
| сырье,м погонный | 1 | ||||
| затраты на заработную плату,т.руб. | 0,349630305 | 1 | |||
| материальные затраты, тыс.руб | 0,830118488 | 0,587647564 | 1 | ||
| амортизация, тыс.руб. | 0,377214053 | 0,759164207 | 0,612169366 | 1 | |
| полная себестоимость, тыс.руб | 0,678604269 | 0,909886866 | 0,825715323 | 0,8247215 | 1 |
Таблица 3
Для определения наличия мультиколлениарности и устранения мультиколлениарных признаков была построена и проанализирована матрица парных коэффициентов корреляции, см. таблица 3.
Матрица парных коэффициентов корреляции
Расчет производился в оболочке «Excel», Сервис → Анализ данных → Корреляция.
Из таблицы 3 видно, что между факторными признаками Сырье и Материальные затраты коэффициент корреляции больше 0,8. Для устранения мультиколлинеарности необходимо исключить из корреляционной модели один из этих признаков, расчеты приведены в таблицах 4 и 5.
Матрица парных коэффициентов корреляции для модели без «Материальных затрат»
|
| сырье, м погонный | затраты на оплату труда, тыс.руб. | амортизация, тыс.руб. | полная себестоимость, тыс.руб |
| сырье, м погонный | 1 | |||
| затраты на оплату труда, тыс.руб. | 0,349630305 | 1 | ||
| амортизация, тыс.руб. | 0,377214053 | 0,759164207 | 1 | |
| полная себестоимость, тыс.руб | 0,678604269 | 0,909886866 | 0,824721504 | 1 |
Таблица 4
Матрица парных коэффициентов корреляции для модели без «Сырья»
|
| затраты на оплату труда, тыс.руб. | материальные затраты, тыс.руб | амортизация, тыс.руб. | полная себестоимость, тыс.руб |
| затраты на оплату труда ,тыс.руб. | 1 | |||
| материальные затраты, тыс.руб | 0,587647564 | 1 | ||
| амортизация, тыс.руб. | 0,759164207 | 0,612169366 | 1 | |
| полная себестоимость, тыс.руб | 0,909886866 | 0,825715323 | 0,824721504 | 1 |
Таблица 5
В обеих моделях теперь отсутствует проблема мультиколлениарности, т.к. все парные коэффициенты между факторными признаками < 0,8.
Так как коэффициент корреляции r между результативным и факторными признаками больше > 0,3, то все признаки дальше участвуют в анализе.
Какую из этих двух модель необходимо выбрать покажет дальнейший анализ.
Для определения признаков рассчитали tрасчетное и взяли tтабличное,см. таблицы 6 и 7.
Матрица расчетных значений t – критерия Стьюдента
для модели без «Материальных затрат»
|
| сырье, м погонный | затраты на оплату труда, тыс.руб. | амортизация, тыс.руб. | полная себестоимость, тыс.руб |
| сырье, м погонный | ||||
| Затраты на оплату труда, тыс.руб. | 1,237707018 | |||
| амортизация, тыс.руб. | 1,350871631 | 3,868284073 | ||
| полная себестоимость, тыс.руб | 3,064211348 | 7,274210595 | 4,836609752 | |
| tтабличное | 2,200985159 |
Таблица 6
Матрица расчетных значений t – критерия Стьюдента
для модели без «Сырья»
|
| затраты на оплату труда,тыс.руб. | материальные затраты, тыс.руб | амортизация, тыс.руб. | полная себестоимость ,тыс.руб |
| затраты на оплату труда тыс.руб. | ||||
| материальные затраты, тыс.руб | 2,408806699 | |||
| амортизация, тыс.руб. | 3,868284073 | 2,567683844 | ||
| полная себестоимость, тыс.руб | 7,274210595 | 4,854902951 | 4,836609752 | |
| tтабличное | 2,200985159 |
Таблица 7
Расчет производился в оболочке «Excel» вручную по формуле (1), tтабличное рассчитывалось с помощью функции СТЬЮДРАСПОБР исходя из той же формулы.
Выводы: в результате сравнения tрасчетное и tтабличное выяснилось, что с вероятностью 0,95 можно утверждать , что связь между результативным и факторными признаками является существенной (tрасчетное › tтабличное), неслучайной. Какую из этих двух модель лучше выбрать покажет дальнейший анализ.
Похожие работы
... Теория очередей 59,7 Нелинейное программирование 46,8 Динамическое программирование 38,7 Теория игр 30,6 Следует отметить определенную переоценку значимости экономико-математических моделей в реальной практике управления экономико-производственными системами. Это связано с непреодолимыми пока сложностями моделирования процессов в экономико-производственных системах из-за непрерывности ...
... z = х47 - х45 -> шах. Глава 2. Определение структурных сдвигов и эффективности оптимального плана 2.1 Анализ оптимального решения экономико-математической модели оптимизации производственной структуры сельскохозяйственного предприятия Экономикс - математический анализ представляет собой заключительный этап математического моделирования экономических процессов, который основывается на ...
... ситуации является определяющим фактором [7]. В зависимости от того, какой метод анализа модели выбран, факторныe разложения могут различаться. Глава 2. Применение детерминированных экономико-математических моделей и методов факторного анализа на примере РУП «ГЗЛиН». 2.1 Характеристика РУП «ГЗЛиН» 9 октября 1979 - издан приказ М 272 Министерства машиностроения для животноводства и ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
0 комментариев