Навигация
Приведение к нормальной форме Коши
1.1 Приведение к нормальной форме Коши
Нормальной формой Коши принято называть общую форму записи ОДУ, то есть представление в виде системы ![]() дифференциальных уравнений первого порядка:
дифференциальных уравнений первого порядка:
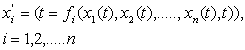 (1)
(1)
ДУ второго порядка, заданное согласно варианту №3 имеет вид:
![]() (2)
(2)
Задание предполагает нахождение решения ![]() на интервале
на интервале ![]() при следующих начальных условиях:
при следующих начальных условиях:
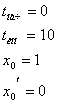 (3)
(3)
Для решения ДУ его просто необходимо представить согласно нормальной формы Коши. Для этого руководствуемся следующими обозначениями:
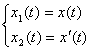 (4)
(4)
В итоге имеется система ДУ первого порядка вида:
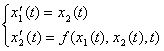 (5)
(5)
Произведя все вышеописанные манипуляции над заданным в варианте уравнением, получим следующую систему:
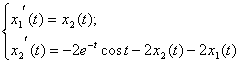 (6)
(6)
Система (6) есть решение уравнения (2).
1.2 Метод Рунге-Кутты второго порядка
В методах Рунге-Кутты интеграл заменяется линейной комбинацией значений подынтегральной функции, вычисленных при разных значениях аргумента:
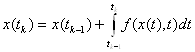 (7)
(7)
Метод Рунге-Кутты представим в виде:

(8)
Из вышеуказанных общих формул (8) получают формулы метода Рунге-Кутты 2-ого порядка m=2;
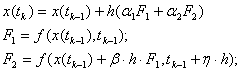 (9)
(9)
Для определения метода необходимо найти значения вещественных коэффициентов: ![]() . Для этого интеграл, заменяемый линейной комбинацией значений подынтегральной функции, вычисленных при разных значениях аргумента, можно представить как:
. Для этого интеграл, заменяемый линейной комбинацией значений подынтегральной функции, вычисленных при разных значениях аргумента, можно представить как:
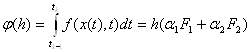 (10)
(10)
А его, в свою очередь, можно представить рядом Тейлора:
![]() (11)
(11)
где ![]() - сумма элементов ряда Тейлора, степень которых не ниже 3.
- сумма элементов ряда Тейлора, степень которых не ниже 3.
Осталось найти неизвестные значения ![]()
 (12)
(12)
В результате таких бесхитростных манипуляций получаем искомый ряд Тейлора:
![]() (13)
(13)
Приравняем коэффициенты при одинаковых степенях ![]() в выражениях
в выражениях
(11) и (13). В итоге получим систему уравнений вида:
 (14)
(14)
Из свойств системы (14) следует отметить, что она не обладает единственным решением. При ![]() значение
значение ![]() , значение
, значение ![]() , а
, а ![]() (15)
(15)
Подставив полученные коэффициенты в соотношение (8), получаем следующие формулы метода Рунге-Кутты 2-ого порядка:
![]()
![]() (16)
(16)
2 ОПИСАНИЕ ПРОГРАММНЫХ МОДУЛЕЙ
Составленная в ходе курсовой работы программа вычисляет решения дифференциального уравнения, с предварительно заданными начальными условиями. Интегрирование происходит согласно двум методам: Рунге-Кутты второго и четвертого порядков.
Программа состоит из следующих модулей:
1) Основная программа;
2) Процедура вычисления точного решения ДУ;
3) Процедура вычисления правых частей;
4) Процедура выполняющая шаг интегрирования методом Рунге-Кутты 2-ого порядка;
5) Процедура выполняющая шаг интегрирования методом Рунге-Кутты 4-ого порядка.
Похожие работы
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... целесообразной также и автоматизация самого процесса получения экспериментальных данных. В следующей главе будет рассмотрена аппаратная часть комплекса для кинетических измерений. ГЛАВА 2. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ КИНЕТИКИ БЫСТРЫХ РЕАКЦИЙ В РАСТВОРЕ Среди различных способов изучения кинетики быстрых реакций выделяется группа методов, отличающаяся некоторыми общими особенностями ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
... * 0─────── 7 8 0 t (1.2.18) 7a 9 0 7a 0 70 0 7 9 0 7 a 0 7 0 Для создания демонстрационной программы удобнее использовать формулу не для x , а для 7D 0x , 1 7{ 0 7b 0+ 7g 0 7}{ 0 4- 7a 4t 0 7} 0 7 b 0+ 7 g 7D 0x=x-x 40 0= ─── 72 0V 40 0- ───── ...

0 комментариев