Навигация
2.1 Основная программа
Блок программы осуществляет следующие операции:
· запрашивает у нерадивого пользователя величину шага интегрирования и шаг вывода на экран;
· вычисляет количество шагов;
· с заданным шагом вызывает процедуры интегрирования методом Рунге-Кутты 2-ого и 4-ого порядков на отрезке интегрирования;
· вычисляет погрешность и оценку погрешности интегрирования;
· выводит замечательные результаты работы программы с заданным шагом вывода на экран.
Для простоты понимания укажем следующие переменные, содержащиеся в программе:
· h - шаг интегрирования. Вводится нерадивым пользователем с клавиатуры;
· n – число шагов интегрирования;
· h_screen - шаг вывода результатов на экран. Вводится нерадивым пользователем с клавиатуры;
· i_screen – счётчик вывода результатов на экран. Когда i_screen > h_screen, то происходит вывод результатов и обнуление i_screen;
· i, j – переменные, используемые циклом;
· e2, e4– ошибки интегрирования для методов Рунге-Кутты 2-ого и 4-ого порядков соответственно. Подсчитываются из соотношения(1):
(1)
· e2max, e4max – оценки погрешностей интегрирования для методов Рунге-Кутты 2-ого и 4-ого порядков соответственно. Подсчитываются из соотношения(2):
(2)
· t – значения независимой переменной;
· t0, tf – пределы интегрирования
· y2, y4 – вектора решения для методов Рунге-Кутты 2-ого и 4-ого порядка соответственно в узле tk;
· outfile– переменная файлового типа. Определена для вывода результатов в текстовой файл;
· name – переменная строкового типа. Используется для передачи имени файла.
Текст основной программы приведён в приложении А, схема в приложении Б.
2.2 Функция вычисления точного решения
function clearsolve (t: real): real
Функция предназначена для вычисления точного решения для дифференциального уравнения по формуле (3):
(3)
Текст функции приведен в приложении 2, схема в приложение 7.
2.3 Процедура вычисления правых частей системы уравнений в нормальной форме Коши
procedure right(t: real; var x,f: vector_n);
Процедура вычисляет правые части системы однородных дифференциальных уравнений в нормальной форме Коши по формуле 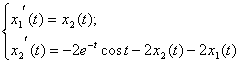(4):
(4)
Текст процедуры приведен в приложении А, а схема в приложение Б.
2.4 Процедура RK2
procedure RK2(t: real; h: real; var x: vector_n);
Укажем формальные параметры:
t – независимая переменная ;
h – шаг интегрирования;
x – массив решений. При входе в процедуру решение в текущем узле интегрирования, при выходе в следующем.
Процедура RK2 выполняет шаг интегрирования системы ОДУ методом Рунге-Кутты 2-ого порядка из соотношения (5):
(5)
где
(6)
Процедура обращается к процедуре вычисления правых частей right с различными параметрами для вычисления 
и 
(6). Затем с Божьей помощью (5) считает значение 
.
Текст процедуры приведен в приложении А, схема в приложение Б.
2.5 Процедура RK4
procedure RK4(t: real; h: real; var x_4: vector_n);
Формальные параметры:
t – независимая переменная ;
h – шаг интегрирования;
x – массив решений. При входе в процедуру решение в текущем узле интегрирования, при выходе в следующем.
Процедура RK4 выполняет шаг интегрирования системы обыкновенных дифференциальных уравнений (1.1.2) методом Рунге-Кутты 4-ого порядка (7).
(7)
где
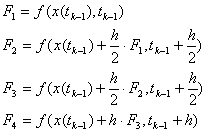(8)
Процедура четыре раза обращается к процедуре вычисления правых частей right с разными параметрами для вычисления ,,
,
(8). Затем с Божьей помощью (7) считает значение .
Текст процедуры приведен в приложении А, схема в приложение Б.
Похожие работы
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... целесообразной также и автоматизация самого процесса получения экспериментальных данных. В следующей главе будет рассмотрена аппаратная часть комплекса для кинетических измерений. ГЛАВА 2. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ КИНЕТИКИ БЫСТРЫХ РЕАКЦИЙ В РАСТВОРЕ Среди различных способов изучения кинетики быстрых реакций выделяется группа методов, отличающаяся некоторыми общими особенностями ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
... * 0─────── 7 8 0 t (1.2.18) 7a 9 0 7a 0 70 0 7 9 0 7 a 0 7 0 Для создания демонстрационной программы удобнее использовать формулу не для x , а для 7D 0x , 1 7{ 0 7b 0+ 7g 0 7}{ 0 4- 7a 4t 0 7} 0 7 b 0+ 7 g 7D 0x=x-x 40 0= ─── 72 0V 40 0- ───── ...
0 комментариев