Сравнительный анализ эффективности методов Рунге-Кутты при различных требованиях к точности вычисления

3.4 Сравнительный анализ эффективности методов Рунге-Кутты при различных требованиях к точности вычисления

 

Для анализа надлежит оценить затраты машинного времени на интегрирование ДУ в зависимости от величины погрешности интегрирования.

Так как для довольно непростых уравнений львиная доля времени уходит на вычисление правых частей уравнений, то в качестве оценки затрат машинного времени можно принять количество вычислений правых частей при нахождении решения на всём отрезке интегрирования, что есть произведение количества шагов интегрирования на порядок метода. Зависимость оценки ошибки интегрирования от количества шагов интегрирования определена.

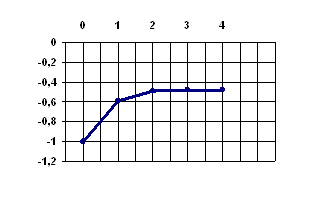
Замечательные результаты вычислений на ПЭВМ приведены все в том же приложении В. Результат работы программы представлены графически (рисунок 5).

 

Рисунок 6 – График зависимости величины ошибки интегрирования от количества вычислений правой части

Из близлежащего графика практически определяется метод для различных требованиях к точности и времени работы нашей замечательной программы. График наглядно демонстрирует, что наличествует такой предел шага, ниже которого программа гоняет свои байты зря, так как оценка погрешности растёт из-за ошибки вычисления ПЭВМ. Стало быть, на практике следует выбирать определенный промежуток шага, желательно в котором алгоритм устойчив.

ЗАКЛЮЧЕНИЕ

При реализации на практике задания для курсовой работы, заключающегося в интегрирования ОДУ, была составлена и отлажена программа, приведенная в приложении А. С помощью данной программы проведена серия опытных исследований свойств методов Рунге-Кутты второго и четвёртого порядков.

При задании определенного интервала значений шага интегрирования ошибка интегрирования уменьшается с уменьшением шага. Подтверждение сего факта можно без труда найти в теории. Однако нельзя обойти вниманием тот труднооспоримый аргумент, что для довольно незначительных значений  с уменьшением шага интегрирования ошибке свойственно увеличивается. Это связано с лавинообразным ростом числа требуемых для получения решения вычислений и c увеличением ошибки вычислений.

На заданном интервале значений  (при условии, что на интервале ошибка вычислений велика не до безобразия), при одинаковых значениях шага интегрирования метод Рунге-Кутты четвёртого порядка имеет достаточно малую ошибку вычисления относительно ошибки метода Рунге-Кутты второго порядка.

Следует отметить, что коэффициент  (формула (1) раздела 3) для таких значений шага интегрирования, при которых можно скрипя сердцем считать его неизменным, имеет меньшее значение для метода Рунге-Кутты четвёртого, нежели второго порядка. Отсюда мораль: ошибка интегрирования с помощью метода Рунге-Кутты четвёртого порядка меньше ошибки интегрирования при использовании метода Рунге-Кутты второго порядка и обусловлено это не только тем, что она обратно пропорциональна величине шага в четвёртой, а не во второй степени, но и оттого, что коэффициент пропорциональности при этом существенно меньше.

Метод Рунге-Кутты четвёртого порядка имеет значительно меньшую ошибку вычисления, нежели метод Рунге-Кутты второго порядка (при условии идентичных машинных затрат). При неизменной требуемой точности для метода Рунге-Кутты четвёртого порядка необходимы меньшие затраты машинного времени относительно метода Рунге-Кутты второго порядка, отчего при корректном выборе шага интегрирования метод Рунге-Кутты четвёртого порядка значительно результативнее, чем метод Рунге-Кутты второго порядка.

БИБЛИОГРАФИЯ

1          Самарский А.А., Гулин А.В. Численные методы .М.: Наука, ГРФМЛ, 1989.- 432с.

2          Бахвалов Н.С. Численные методы. М.: Наука, ГРФМЛ,1987.-600 с.

3          Ляшко И.И., Макаров В.Л. Интегральные методы вычислений. Киев, 1977, 408с.

4          Мантуров О.В. Курс высшей математики М.:В.Ш.-1991.-448с.

5          Маликов В.Т. Вычислительные методы и применение Киев: В.Ш.-1989.-213 с.

ПРИЛОЖЕНИЕ А

(Справочное)

 

Основная программа

 

program DU(input,output);

 uses crt;

 type vector_n = array [1..2] of real;

 var t0, tf, k, j, n: integer;

t, yt, h, h_screen, e2, e4, e2max, e4max, i_screen: real;

y2, y4: vector_n;

name: string;

outfile: text;

begin

 clrscr;

 writeln('Please enter file name');

 readln(name);

 writeln('Please enter h,h_screen');

 readln(h,h_screen);

 clrscr;

 writeln;

 assign(outfile,name);

 rewrite(outfile);

 t0:=0;

 tf:=10;

 n:=round((tf-t0)/h);

 y2[1]:=1;

 y2[2]:=0;

 y4:=y2;

 e2:=0;

 e4:=0;

 e2max:=0;

 e4max:=0;

 t:=t0;

 i_screen:=h_screen;

 for k:=0 to n do

 begin

 yt:=clearsolve(t);

 e2:=abs(yt-y2[1]);

 e4:=abs(yt-y4[1]);

 if e2>e2max then e2max:=e2;

 if e4>e4max then e4max:=e4;

 if i_screen>h_screen-0.00001 then

 begin

yt:=clearsolve (t);

e2:=abs(yt-y2[1]);

e4:=abs(yt-y4[1]);

if e2>e2max then e2max:=e2;

if e4>e4max then e4max:=e4;

if i_screen>h_screen-0.00001 then

begin

writeln(' t=',t:6:3,'; yt=',yt:9:3,'; y2=',y2[1]:9:3,'; y4=',y4[1]:9:3,'; e2=',e2:6:3,'; e4=',e4:8:6);

writeln(outfile,' t=',t:10:6,'; yt=',yt:10:6,'; y2=',y2[1]:10:6,'; y4=',y4[1]:10:6,'; e2=',e2:12:9,'; e4=',e4:12:9,'.');

i_screen:=0;

end;

if t+h>tf-0.000001 then

 begin

 h:=tf-t;

 t:=tf-h;

 i_screen:=h_screen;

 end;

 RK2(t,h,y2);

 RK4(t,h,y4);

 t:=t+h;

 i_screen:=i_screen+h;

 end;

 writeln;

 writeln(' h=',(h):8:5,'; e2max=',e2max:16:8,'; e4max=',e4max:16:8,' ',n:8);

 writeln(outfile);

 writeln(outfile,' h=',h:6:5,'; e2max=',e2max:10:8,'; e4max=',e4max:10:8,'.');

 close(outfile);

 readkey;

end.

Функция вычисления точного решения

function clearsolve(t:real):real;

 begin

 clearsolve:=exp(-t)*(cos(t)+sin(t)+t*sin(t));

 end;

Процедура вычисления правых частей системы уравнений в нормальной форме Коши

procedure right(t:real;var x,f:vector_n);

 begin

 f[1]:=x[2];

 f[2]:=2*exp(-t)*cos(t)-2*x[1]-2*x[2];

 end;

 

Процедура RK2

procedure RK2(t:real;h:real;var x:vector_n);

 var h4, h23: real;

f1, f2, xr: vector_n;

 begin

 h4:=0.25*h;

 h23:=0.66666667*h;

 right(t,x,f1);

 for j:=1 to 2 do xr[j]:=x[j]+h23*f1[j];

 right(t+h23,xr,f2);

 for j:=1 to 2 do x[j]:=x[j]+h4*(f1[j]+3*f2[j]);

end;

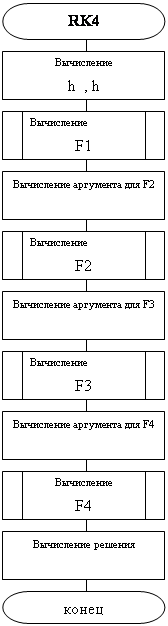
Процедура RK4

procedure RK4(t:real;h:real;var x:vector_n);

var h2,h6:real;

f,fs,xr:vector_n;

begin

 h2:=0.5*h;

 h6:=0.166666667*h;

 right(t,x,fs);

for j:=1 to 2 do xr[j]:=x[j]+h2*fs[j];

 right(t+h2,xr,f);

for j:=1 to 2 do

 begin

 xr[j]:=x[j]+h2*f[j];

 fs[j]:=fs[j]+2*f[j];

 end;

 right(t+h2,xr,f);

 for j:=1 to 2 do

 begin

 xr[j]:=x[j]+h*f[j];

 fs[j]:=fs[j]+2*f[j];

 end;

 right(t+h,xr,f);

 for j:=1 to 2 do

 x[j]:=x[j]+h6*(f[j]+fs[j]);

end;

ПРИЛОЖЕНИЕ Б

(Справочное)

Схема основной программы

 

Схема функции вычисления точного решения

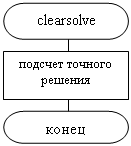
Схема процедуры вычисления правых частей системы уравнений в нормальной форме Коши

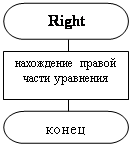
Схема процедуры RK2

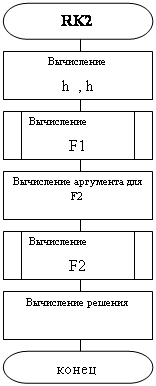
Схема процедуры RK4

ПРИЛОЖЕНИЕ В

(Справочное)

 

Результаты экспериментов

 

t= 0.000000; yt= 1.000000; y2= 1.000000; y4= 1.000000; e2=0.000000; e4=0.000000

t= 0.400000; yt= 0.982855; y2= 0.983425; y4= 0.982856; e2=0.000570; e4=0.000001

t= 0.800000; yt= 0.893242; y2= 0.893209; y4= 0.893244; e2=0.000033; e4=0.000001

t= 1.200000; yt= 0.726735; y2= 0.725954; y4= 0.726735; e2=0.000781; e4=0.000001

t= 1.600000; yt= 0.518812; y2= 0.517695; y4= 0.518812; e2=0.001117; e4=0.000000

t= 2.000000; yt= 0.312861; y2= 0.311906; y4= 0.312860; e2=0.000955; e4=0.000001

t= 2.400000; yt= 0.141446; y2= 0.140967; y4= 0.141444; e2=0.000479; e4=0.000001

t= 2.800000; yt= 0.020112; y2= 0.020173; y4= 0.020111; e2=0.000062; e4=0.000001

t= 3.200000; yt= 0.050686; y2=-0.050207; y4=-0.050687; e2=0.000480; e4=0.000001

t= 3.600000; yt=-0.080123; y2=-0.079431; y4=-0.080123; e2=0.000692; e4=0.000001

t= 4.000000; yt=-0.081279; y2=-0.080573; y4=-0.081279; e2=0.000705; e4=0.000000

t= 4.400000; yt=-0.066862; y2=-0.066283; y4=-0.066862; e2=0.000579; e4=0.000000

t= 4.800000; yt=-0.046829; y2=-0.046441; y4=-0.046829; e2=0.000388; e4=0.000000

t= 5.200000; yt=-0.027632; y2=-0.027436; y4=-0.027632; e2=0.000196; e4=0.000000

t= 5.600000; yt=-0.012539; y2=-0.012497; y4=-0.012538; e2=0.000042; e4=0.000000

t= 6.000000; yt=-0.002468; y2=-0.002527; y4=-0.002468; e2=0.000058; e4=0.000000

t= 6.400000; yt= 0.003083; y2= 0.002977; y4= 0.003083; e2=0.000106; e4=0.000000

t= 6.800000; yt= 0.005261; y2= 0.005147; y4= 0.005261; e2=0.000113; e4=0.000000

t= 7.200000; yt= 0.005313; y2= 0.005217; y4= 0.005313; e2=0.000096; e4=0.000000

t= 7.600000; yt= 0.004292; y2= 0.004223; y4= 0.004292; e2=0.000068; e4=0.000000

t= 8.000000; yt= 0.002938; y2= 0.002898; y4= 0.002938; e2=0.000040; e4=0.000000

t= 8.400000; yt= 0.001690; y2= 0.001673; y4= 0.001690; e2=0.000017; e4=0.000000

t= 8.800000; yt= 0.000742; y2= 0.000741; y4= 0.000742; e2=0.000001; e4=0.000000

t= 9.200000; yt= 0.000131; y2= 0.000139; y4= 0.000131; e2=0.000008; e4=0.000000

t= 9.600000; yt=-0.000192; y2=-0.000181; y4=-0.000192; e2=0.000011; e4=0.000000

t=10.000000; yt=-0.000310; y2=-0.000299; y4=-0.000310; e2=0.000010; e4=0.000000

h=0.00000; e2max=0.00111851; e4max=0.00000132.