Огляд і варіантний аналіз чисельних методів моделювання термопари
Класифікація методів
Сплайн-інтерполяція
Розробка алгоритмів моделювання зміни температури термопари за допомогою чисельних методів на ЕОМ
Опис основних функцій моделювання
Розробка тестів та аналіз результату тестування
Оцінка похибок результатів експериментальних досліджень
Навигация
Сплайн-інтерполяція
Дослідження зміни температури термопари за допомогою чисельних методів на ЕОМ
57641
знак
6
таблиц
20
изображений
1.3.5 Сплайн-інтерполяція
Сплайн – це група сполучених кубічних багаточленів, в місцях сполучення яких перша та друга похідні безперервні. Такі функції звуться кубічними сплайнами. Для їх побудування необхідно задати коефіцієнти, які однозначно визначають поліном у проміжку між двома точками.
Наприклад, у випадку, який показаний на рисунку 1.3.1, необхідно задати всі кубічні функції 
В найбільш загальному випадку ці багаточлени мають такий вигляд:
i=1,2, ... ,m (1.25)
де 
– постійні, які визначені вказаними умовами (j= 1,2,3,4).
Перші (2m) умов потребують, щоб сплайни стикалися в заданих точках:
,i=1, 2, ... , m,
, i=0, 1, ... , m-1. (1.26)
Наступні (2m-2) умов потребують, щоб в місцях дотику сплайнів були рівні перші та другі похідні
i=1, ... , m-1, (1.27)
i=1, ... , m-1.
Система алгебраїчних рівнянь має розв’язок, якщо кількість рівнянь дорівнює кількості невідомих. Для цього необхідні ще два рівняння. Як правило, використовують такі додаткові умови:
(1.28)
Отриманий таким чином сплайн зветься “природним кубічним сплайном”.
В багатьох випадках метод сплайнів є найбільш зручним, тому що це дозволяє отримати аналітичну кусково-поліноміальну функцію. Існують сплайни більш вищих порядків. Вживання цього методу можливо і в інших галузях обчислювальної математики, наприклад, в чисельному інтегруванні і розв’язанні диференціальних рівнянь.
1.4 Уточнена постановка задачі
Нехай на відрізку [а; b] визначено певний клас функцій {Р(х)}, наприклад клас алгебраїчних многочленів, а в точках х0, х1,..., хn цього проміжку задано значення деякої функції y=f(x): y0=f(x0), y1=f(x1),….yn=f(xn). Наближену заміну функції f на відрізку [а; b] однією з функцій Р(х) цього класу так, щоб функція P(х) в точках x0,x1, ..., xn набувала тих самих значень, що й функція f, тобто щоб Р(xi)= уi (і = 0, 1, ..., n), називають інтерполюванням, або інтерполяцією. Точки х0, хi, ..., хп називають вузлами інтерполювання, функцію Р(х) — інтерполюючою функцією, а формулy у=P(х), за допомогою якої обчислюють значення функції f у проміжку [а;b], — інтерполяційною формулою.
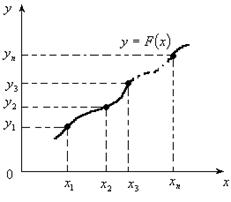
З геометричного погляду задача інтерполювання полягає в знаходженні кривої у= Р(х) певного класу, яка проходить через точки площини з координатами (хi, уi)
(i = 0, 1, ....,n) (рис.1.1.1).
Якщо функція Р(х) належить класу алгебраїчних многочленів, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати й інтегрувати.
У деяких випадках доцільніше використовувати інші класи інтерполюючих функцій. Якщо, наприклад, функція f періодична, то функцію Р(х) природно вибирати з класу тригонометричних многочленів, а якщо функція f перетворюється в нескінченність у заданих точках або поблизу них, то функцію Р(х) доцільно вибирати з класу раціональних функцій.
Розглядатимемо лише задачу параболічного інтерполювання, яку сформулюємо так: в n+1 різних точках х0, x1,..., хn задано значення
функції f: y0=f(x0), y1=f(x1),…, yn=f(xn) і треба побудувати многочлен
(1.29)
степеня n, який задовольняв би умови
(1.30)
Для визначення n+1 коефіцієнтів многочлена (1.29), який задовольняє умови (1.30), запишемо систему (n+1)-го лінійних рівнянь виду:
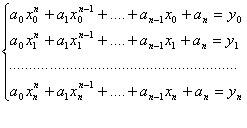(1.31)
Ця система має єдиний розв'язок, бо її визначник є визначником Вандермонда, який не дорівнює нулю, бо вузли xi=(i=0,1,…,n) різні. А тому й задача параболічного інтерполювання має єдиний розв'язок, тобто існує єдиний алгебраїчний многочлен виду (1.29), що задовольняє умови (1.30). Многочлен Рn(х), який задовольняє умови (1.29), називають інтерполяційним многочленом, наближену рівність f(x)=Pn(x) –
інтерполяційною формулою, а різницю Rn(f,x)=f(x) – Pn(x) — залишковим членом інтерполяційної формули. Хоч інтерполяційний многочлен, що задовольняє умови (1.29), і єдиний, проте можливі різні форми його запису.
Інтерполяційний многочлен будують тоді, коли:
1) функцію задано таблично для деяких значень аргументу, а треба знайти її значення для значень аргументу, яких у таблиці немає;
2) функцію задано графічно, наприклад за допомогою самописного приладу, а треба знайти її наближений аналітичний вираз;
3) функцію задано аналітичнo, але її вираз досить складний і незручний для виконання різних математичних операцій (диференціювання, інтегрування тощо).
Похожие работы
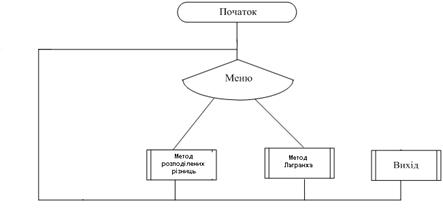
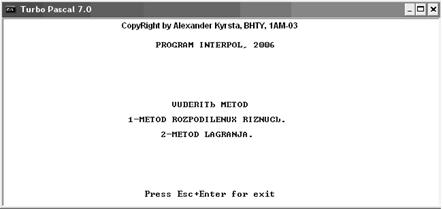
... Interpol. Для запуску програми необхідно запустити файл Interpol. exe. Після запуску програми з’являється меню, реалізоване в текстовому режимі, яке дозволяє вибрати необхідний метод інтерполяції. Для вибору методу розподілених різниць необхідно натиснути клавішу "1", для вибору методу Лагранжа - клавішу "2". Після вибору методу для графічного представлення результатів інтерполяції функції в ...
... Методичні вказівки до лабораторної роботи № З «Тепловіддача горизонтальної труби при вільному русі повітря». Тернопіль 2003 У даних методичних вказівках подані теоретичні основи, опис експернментальної установки і практичні рекомендації лля проведення лабораторної роботи і обробки дослідних даних Мета роботи - засвоїти знання з теорії" конвсктивнот теплообміну при ...
... ї зони та обмеження доступу до неї людей. На підприємстві згідно з вимогами законодавчих та інших нормативно-правових актів з питань захисту населення і територій від надзвичайних ситуацій та охорони праці повинні бути розроблені і затверджені роботодавцем: - план попередження надзвичайних ситуацій, у якому визначаються можливі аварії та інші надзвичайні ситуації техногенного та природного ...
... підвищенням гнучкості технологічних систем, застосуванням машин з числовим програмним керуванням, впровадженням автоматичних багатофункціональних маніпуляторів-роботів. РОЗДІЛ 3. ЕКОНОМІЧНЕ ОБҐРУНТУВАННЯ ОСНОВНИХ НАПРЯМКІВ РАЦІОНАЛІЗАЦІЇ ТРУДОВИХ ПРОЦЕСІВ НА ВАТ "ЕЛЕКТРОТЕРМОМЕТРIЯ" Провівши аналіз організації трудових процесів на ВАТ "Електротермометрія", слід було б відмітити, що в 2009 ...
0 комментариев