Навигация
Основные генетические операторы
1.3 Основные генетические операторы
Как известно в теории эволюции важную роль играет то, каким образом признаки родителей передаются потомкам. В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание (его также называют кроссовер или кроссинговер). Этот оператор определяет передачу признаков родителей потомкам. Действует он следующим образом:
o из популяции выбираются две особи, которые будут родителями;
o определяется (обычно случайным образом) точка разрыва;
o потомок определяется как конкатенация части первого и второго родителя.
Рассмотрим функционирование этого оператора
| Хромосома_1: | 0000000000 |
| Хромосома_2: | 1111111111 |
Допустим, разрыв происходит после 3-го бита хромосомы, тогда получаем.
| Хромосома_1: | 0000000000 | >> | 000 | 1111111 | Результирующая хромосома 1 |
| Хромосома_2: | 1111111111 | >> | 111 | 0000000 | Результирующая хромосома 2 |
Итак, рассмотрим все же операторы по порядку:
1) кроссинговер - создание структуры, основанной на двух структурах - заменой одной части первой структуры на ту же область во второй.
Пример: из (A, B, C, D, E) и (a, b, c, d, e) получится (A, B, c, d, E).
Затем с вероятностью 0,5 определяется одна из результирующих хромосом в качестве потомка.
Следующий генетический оператор предназначен для того, чтобы поддерживать разнообразие особей с популяции. Он называется оператором мутации. При использовании данного оператора каждый бит в хромосоме с определенной вероятностью инвертируется. Кроме того, используется еще и так называемый оператор инверсии, который заключается в том, что хромосома делится на две части, и затем они меняются местами. Схематически это можно представить следующим образом:
| 000 | 1111111 | >> | 1111111 | 000 |
2) инверсия - перестановка в структуре некоторой ее части наоборот
Пример: из (1, 1, 0, 1, 0, 0, 1, 0) получится (1, 1, 0, 0, 1, 0, 1, 0).
3) мутация - замена в структуре одного из значений случайно выбранной компоненты
Пример: из (1, 1, 0, 1, 0, 0, 1, 0) получится (1, 1, 0, 1, 1, 0, 1, 0).
В принципе для функционирования генетического алгоритма достаточно этих двух генетических операторов, но на практике применяют еще и некоторые дополнительные операторы или модификации этих двух операторов. Например, кроссовер может быть не одноточечный (как было описано выше), а многоточечный, когда формируется несколько точек разрыва (чаще всего две). Кроме того, в некоторых реализациях алгоритма оператор мутации представляет собой инверсию только одного случайно выбранного бита хромосомы.
1.4. Схема функционирования генетического алгоритма
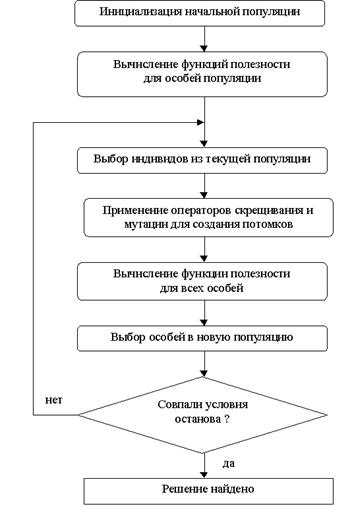
Теперь, зная как интерпретировать значения генов, перейдем к описанию функционирования генетического алгоритма. Рассмотрим схему функционирования генетического алгоритма в его классическом варианте.
Инициировать начальный момент времени t=0 . Случайным образом сформировать начальную популяцию, состоящую из k особей.
Вычислить приспособленность каждой особи и популяции в целом (также иногда называемую термином фиттнес). Значение этой функции определяет насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.
1. Выбрать особь из популяции.
2. С определенной вероятностью (вероятностью кроссовера ) выбрать вторую особь из популяции и произвести оператор кроссовера.
3. С определенной вероятностью (вероятностью мутации) выполнить оператор мутации.
4. С определенной вероятностью (вероятностью инверсии ) выполнить оператор инверсии.
5. Поместить полученную хромосому в новую популяцию
6. Выполнить операции, начиная с пункта 3, k раз.
7. Увеличить номер текущей эпохи t=t+1.
8. Если выполнилось условие остановки, то завершить работу, иначе переход на шаг 2 [13].
Распишем более подробно следующие этапы:
1. Выбор родительской пары .
Первый подход самый простой - это случайный выбор родительской пары ("панмиксия"), когда обе особи, которые составят родительскую пару, случайным образом выбираются из всей популяции, причем любая особь может стать членом нескольких пар. Несмотря на простоту, такой подход универсален для решения различных классов задач. Однако он достаточно критичен к численности популяции, поскольку эффективность алгоритма, реализующего такой подход, снижается с ростом численности популяции.
Второй способ выбора особей в родительскую пару - так называемый селективный. Его суть состоит в том, что "родителями" могут стать только те особи, значение приспособленности которых не меньше среднего значения приспособленности по популяции, при равной вероятности таких кандидатов составить брачную пару. Такой подход обеспечивает более быструю сходимость алгоритма. Однако из-за быстрой сходимости селективный выбор родительской пары не подходит тогда, когда ставиться задача определения нескольких экстремумов, поскольку для таких задач алгоритм, как правило, быстро сходится к одному из решений. Кроме того, для некоторого класса задач со сложным ландшафтом приспособленности быстрая сходимость может превратиться в преждевременную сходимость к квазиоптимальному решению. Этот недостаток может быть отчасти компенсирован использованием подходящего механизма отбора (о чем будет сказано ниже), который бы "тормозил" слишком быструю сходимость алгоритма.
Другие два способа формирования родительской пары, на которые хотелось бы обратить внимание, это инбридинг и аутбридинг. Оба эти метода построены на формировании пары на основе близкого и дальнего "родства" соответственно. Под "родством" здесь понимается расстояние между членами популяции как в смысле геометрического расстояния особей в пространстве параметров. В связи с этим будем различать генотипный и фенотипный (или географический) инбридинг и аутбридинг. Под инбридингом понимается такой метод, когда первый член пары выбирается случайно, а вторым с большей вероятностью будет максимально близкая к нему особь. Аутбридинг же, наоборот, формирует брачные пары из максимально далеких особей. Использование генетических инбридинга и аутбридинга оказалось более эффективным по сравнению с географическим для всех тестовых функций при различных параметрах алгоритма. Наиболее полезно применение обоих представленных методов для многоэкстремальных задач [14]. Однако два этих способа по-разному влияют на поведение генетического алгоритма. Так инбридинг можно охарактеризовать свойством концентрации поиска в локальных узлах, что фактически приводит к разбиению популяции на отдельные локальные группы вокруг подозрительных на экстремум участков ландшафта, напротив аутбридинг как раз направлен на предупреждение сходимости алгоритма к уже найденным решениям, заставляя алгоритм просматривать новые, неисследованные области.
Похожие работы
... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...
... в популяциях, которые являются существенными для развития. Точный ответ на вопрос: какие биологические процессы существенны для развития, и какие нет? - все еще открыт для исследователей. Реализация генетических алгоритмов В природе особи в популяции конкурируют друг с другом за различные ресурсы, такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют ...
... N строк. Для популяции вводится понятие средней ценности популяции Fср (G(t)): Аналогично для подпопуляции GH(t), удовлетворяющей схеме H, вводится понятие средней ценности подпопуляции Fср (GH(t)):. Генетический алгоритм осуществляет переход от популяции G(t) к популяции G(t+1) таким образом, чтобы средняя ценность составляющих её строк увеличивалась, причём количество новых строк в популяции ...
... решения Скрещивание, рекомбинация, кроссинговер Оператор рекомбинации мутация Оператор модификации При разработке генетических алгоритмов преследуется две главные цели: · Абстрактное и формальное объяснение процессов адаптации в естественных системах; · Проектирование искусственных программных систем, воспроизводящих механизмы функционирования естественных систем. Основные отличия ГА от ...
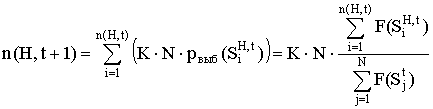
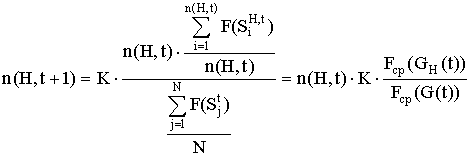
0 комментариев