Навигация
Составляем систему ограничения задачи
2. Составляем систему ограничения задачи
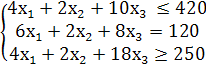
по условию задачи требуется, чтобы
трудовые ресурсы были использованы полностью значит, ставим знак (=), а накладные расходы были бы не менее имеющихся в наличии значит, ставим знак (![]() ).
).
3. Задаём целевую функцию
Z(X) = ![]()
Математическая модель имеет вид: найти план выпуска станков
X = (![]() ),
),
удовлетворяющий системе ограничений задачи
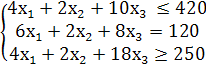
и условию неотрицательности ![]() ), при котором прибыль будет максимальной
), при котором прибыль будет максимальной
Z(X) = ![]()
§ 3 Алгоритмы решения задачи симплексным методом
Общая идея симплексного метода (метода последовательного улучшения плана) для решения задачи линейного программирования состоит
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходит к нехудшему опорному плану.
Алгоритм:
1) Математическая модель задачи должна иметь каноническую форму. В противном случаи её приводят к каноническому виду.
2) Находят начальное опорное решение задачи. Им является вектор, состоящий из тех переменных, которые входят только в одно уравнение в системе ограничений. Если начальное решение сразу не найти то используют метод Гаусса.
Количество переменных решения равно количеству уравнений системы. Заполняют симплексную таблицу по системе ограничений и целевой функции.
Макет симплексной таблицы:
| Б |
|
|
|
|
|
| … |
|
|
|
|
|
|
|
| … |
| |||
| … | |||||||||
| … | |||||||||
| … | … | … | … | … | … | … | … | … | … |
|
| |||||||||
Первый столбец – коэффициенты в целевой функции при базисных переменных.
Второй столбец – базисные переменные.
Третий столбец – свободные члены.
Самая верхняя строка – коэффициенты при целевой функции.
Вторая верхняя строка – сами переменные, входящие в целевую функцию и в систему ограничений.
Основное поле симплекс метода – система коэффициентов из уравнения.
Последняя строка – служит для того, чтобы ответить на вопрос: “оптимален план или нет ”.
Индексная строка позволяет нам судить об оптимальности плана.
3) Проверяют опорное решение, на оптимальность, вычисляя коэффициенты индексной строки по форме:
![]()
При решении задачи возможны два случая:
- При решении задачи на максимум:
а) все оценки ![]() следует, что решение оптимальное
следует, что решение оптимальное
б) хотя бы одна оценка ![]() и при соответствующей переменной нет положительных коэффициентов, то задача не имеет оптимального решения m, k, целевая функция неограниченна в О.Д.Р.
и при соответствующей переменной нет положительных коэффициентов, то задача не имеет оптимального решения m, k, целевая функция неограниченна в О.Д.Р.
в) хотя бы одна оценка ![]() и при соответствующей переменной есть положительный коэффициент то данное решение можно улучшить, построив новое опорное решение на котором целевая функция будет больше.
и при соответствующей переменной есть положительный коэффициент то данное решение можно улучшить, построив новое опорное решение на котором целевая функция будет больше.
- При решении задачи на минимум:
а) все оценки ![]() следует, что решение оптимальное
следует, что решение оптимальное
б) хотя бы одна оценка ![]() и при соответствующей переменной нет положительных коэффициентов, то задача не имеет оптимального решения m, k, целевая функция неограниченна в О.Д.Р.
и при соответствующей переменной нет положительных коэффициентов, то задача не имеет оптимального решения m, k, целевая функция неограниченна в О.Д.Р.
в) хотя бы одна оценка ![]() и при соответствующей переменной есть положительный коэффициент то данное решение можно улучшить, построив новое опорное решение.
и при соответствующей переменной есть положительный коэффициент то данное решение можно улучшить, построив новое опорное решение.
4) Новое опорное решение находится с помощью ключевого столбца, ключевой строки и ключевого элемента.
Ключевой столбец указывает на переменную, которую надо вывести из числа базисных для улучшения решения.
Ключевая строка указывает на переменную, которую надо вывести из числа базисных для улучшения решения.
Ключевой элемент нужен для элементов нового опорного решения (для новой симплексной таблицы).
Их нахождения зависит от цели задачи.
- При решении задачи на максимум:
а) ключевой столбец – это столбец с отрицательной наименьшей оценкой ![]() в индексной строке.
в индексной строке.
б) ключевая строка – это строка с наименьшим отношением свободных членов к положительным коэффициентам ключевого столбца:
min ![]() =
= ![]()
в) ключевой элемент – это число расположенное на пересечении ключевых столбца и строки(не может быть равен нулю).
- При решении задач на минимум:
а) ключевой столбец – это столбец с положительной наименьшей оценкой ![]() в индексной строке.
в индексной строке.
б) ключевая строка – это строка с наибольшим отношением свободных членов к положительным коэффициентам ключевого столбца:
mах ![]() =
= ![]()
в) ключевой элемент – это число расположено на пересечении ключевых столбца и строки.
5) Заполняют первую симплексную таблицу следующим образом:
а) ключевую строку делят на ключевой элемент и записывают на том же месте в новой таблице.
б) заполняют базисные столбцы.
в) остальные элементы пересчитывают по правилу “прямоугольника”:
НЭ = СТЭ – ![]()
где НЭ – новый элемент
СТЭ – элемент старого плана
РЭ – разрешающей элемент
А и Б – элементы старого плана
6) Возвращаются ко второму этапу алгоритма – проверка плана на оптимальность.
§ 4 Построение начального опорного решения методом Гаусса
Приводим задачу к каноническому виду.
Z(X) = ![]()
![]()
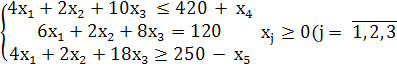 )
)
Z(X) = ![]()
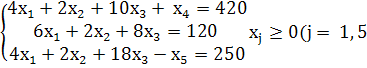 )
)

![]() 4 2 10 1 0 420
4 2 10 1 0 420
6 2 8 0 0 120 * (-1)
![]() 4 2 18 0 -1 250
4 2 18 0 -1 250
28 24 20 0 0 0


![]()
![]() 4 2 10 1 0 420
4 2 10 1 0 420
-6 -2 -8 0 0 -120 + + ![]()
![]() 4 2 18 0 -1 250
4 2 18 0 -1 250
28 24 20 0 0 0

![]() -2 0 2 1 0 420
-2 0 2 1 0 420
6 2 8 0 0 120 *12
![]() -2 0 10 0 -1 130
-2 0 10 0 -1 130
28 24 20 0 0 0

![]() -2 0 2 1 0 300
-2 0 2 1 0 300
72 24 96 0 0 1440 -
![]() -2 0 10 0 -1 130
-2 0 10 0 -1 130
28 24 20 0 0 0

![]() -2 0 2 1 0 300
-2 0 2 1 0 300
72 24 96 0 0 1440 ![]()
![]() -2 0 10 0 -1 130
-2 0 10 0 -1 130
-44 0 -76 0 0 -1440

![]() -2 0 2 1 0 300 *5
-2 0 2 1 0 300 *5
3 1 4 0 0 60
![]() -2 0 10 0 -1 130 * (-1)
-2 0 10 0 -1 130 * (-1)
-44 0 -76 0 0 -1440
 | |||
 | |||
![]() -10 0 10 5 0 1500
-10 0 10 5 0 1500
3 1 4 0 0 60
![]() 2 0 -10 0 1 -130 +
2 0 -10 0 1 -130 +
-44 0 -76 0 0 -1440

![]() -10 0 10 5 0 1500
-10 0 10 5 0 1500 ![]()
3 1 4 0 0 60
![]() 12 0 0 5 1 1370
12 0 0 5 1 1370 ![]()
-44 0 -76 0 0 -1440

![]()
![]() -2 0 2 1 0 300 -
-2 0 2 1 0 300 -
3 1 4 0 0 60
![]() 2,4 0 0 1 1 274
2,4 0 0 1 1 274
-44 0 -76 0 0 -1440

![]() -4,4 0 2 0 -1 26 *2
-4,4 0 2 0 -1 26 *2
3 1 4 0 0 60
![]() 2,4 0 0 1 1 274
2,4 0 0 1 1 274
-44 0 -76 0 0 -1440

![]()
![]() -8,8 0 4 0 -2 52
-8,8 0 4 0 -2 52
3 1 4 0 0 60 -
![]() 2,4 0 0 1 1 274
2,4 0 0 1 1 274
-44 0 -76 0 0 -1440

![]() -8,8 0 4 0 -2 52 *19
-8,8 0 4 0 -2 52 *19
11,8 1 0 0 2 8
![]() 2,4
0 0 1 1 274
2,4
0 0 1 1 274
-44 0 -76 0 0 -1440
![]()

![]() -167,2 0 76 0 -38 988
-167,2 0 76 0 -38 988
11,8 1 0 0 2 8
![]() 2,4 0 0 1 1 274
2,4 0 0 1 1 274
-44 0 -76 0 0 -1440 +

![]() -167,2 0 76 0 -38 988
-167,2 0 76 0 -38 988 ![]()
11,8 1 0 0 2 8
![]() 2,4 0 0 1 1 274
2,4 0 0 1 1 274
-123,2 0 0 0 -38 -452

![]() -2,2 0 1 0 -0,5 13
-2,2 0 1 0 -0,5 13
11,8 1 0 0 2 8
![]() 2,4 0 0 1 1 274
2,4 0 0 1 1 274
-123,2 0 0 0 -38 -452
§ 5 Решение задачи
Составляем симплексную таблицу
Симплексная таблица 1
| Б |
| -452 | -123,2 | 0 | 0 | 0 | -38 |
|
|
|
|
|
|
|
| |||
|
| 0 | 13 | -2,2 | 1 | 0 | 0 | -0,5 | |
|
| 0 | 8 | 11,8 | 1 | 0 | 0 | 2 | |
|
| 0 | 274 | 2,4 | 0 | 0 | 1 | 1 | |
|
| 452 | 123,2 | 0 | 0 | 0 | 38 | ||
![]()

т. к все ![]() > 0 решение оптимальное
> 0 решение оптимальное
Ответ: max Z(X) = 452 при X = (0; 8; 13)
§ 6 Вывод
Максимальная прибыль в размере 425 тыс. руб. может быть достигнута, если производить 8 станков ІΙ вида, 13 станков ІΙІ вида и не производить станки Ι вида.
При этом расходуется 146 ед. сырья, 120 ед. трудовых ресурсов и 250 ед. накладных расходов.
Заключение
Данная курсовая работа посвящена вопросу о решении задачи линейного программирования методом последовательного улучшения плана, иначе симплекс – метод. Состоит из введения, двух глав, заключения и списка литературы.
В первой главе рассказывается о линейном программировании в частности, и о том, что такое общая постановка задачи линейного программирования, как составить математическую модель, а также рассказано о канонической форме задач линейного программирования.
Вторая глава работы посвящена практической части решения задачи. Строится математическая модель, решается задача симплексным методом, а также методом Гаусса.
Похожие работы
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...










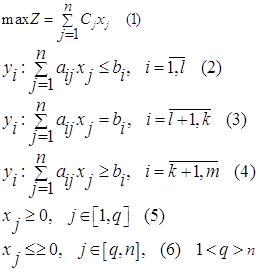
0 комментариев