Навигация
РАСЧЁТ БАКА НА ПРОЧНОСТЬ
5. РАСЧЁТ БАКА НА ПРОЧНОСТЬ
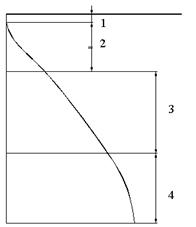
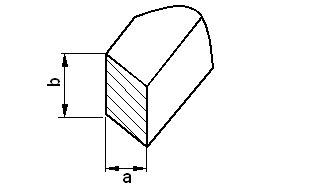
Условие задачи: Цилиндрический бак с верхним полуэллиптическим и нижним полусферическими днищами (рис.1) находится под действием давления наддува ![]() и заполнен жидкостью до уровня H.
и заполнен жидкостью до уровня H.
Цель расчёта:
1. Определить величину безмоментных напряжений ![]() ;
;
2. Определить толщину обечайки и днищ бака.
Исходные данные:
Радиус бака: ![]() м;
м;
Размеры эллиптического днища: ![]()
![]()
Высота столба жидкости: ![]() ;
;
Плотность жидкости (окислитель): ![]() ;
;
Давление наддува: ![]() ;
;
Коэффициент безопасности: ![]() ;
;
Материал оболочки:
марка ВТ6С (О);
предел прочности ![]() ;
;
![]() .
.
Выполнение расчёта
Участок верхнего эллиптического днища
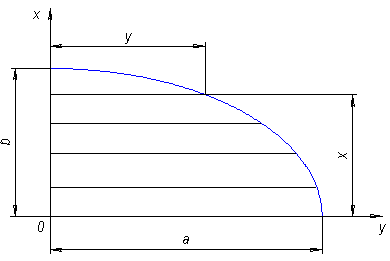
Рис. 2. Схема эллиптического днища
В днище нормальным коническим сечением I – I отсечём верхнюю часть оболочки и составим для неё уравнение равновесия. Выбираем оси координат так, как показано на рис. 2. Из уравнения равновесия и уравнения Лапласа получаем выражения для ![]() в расчётном сечении эллиптического днища в виде:
в расчётном сечении эллиптического днища в виде:
![]()
![]() ,
,
где ![]() ,
, ![]() – радиусы кривизны рассматриваемого сечения оболочки,
– радиусы кривизны рассматриваемого сечения оболочки,
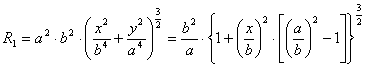 ,
,
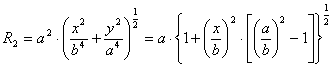 ,
,
где x, y – координаты точки в рассматриваемом сечении оболочки.
Для построения эпюр задаёмся значениями x. Координату y определяем из уравнения эллипса ![]() . Отсюда получаем
. Отсюда получаем
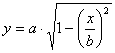 .
.
Меньшую полуось b разбиваем на 5 равных частей, для каждого сечения производим расчёты, результаты расчётов заносим в таблицу 1.
Таблица 1
| № сечения | x, м | y, м | R1, м | R2, м |
|
|
| 1 | 0 | 1,125 | 0,18 | 1,125 |
|
|
| 2 | 0,09 | 1,102 | 0,24 | 1,238 |
|
|
| 3 | 0,18 | 1,031 | 0,449 | 1,526 |
|
|
| 4 | 0,27 | 0,9 | 0,884 | 1,913 |
|
|
| 5 | 0,36 | 0,675 | 1,639 | 2,349 |
|
|
| 6 | 0,45 | 0 | 2,813 | 2,813 |
|
|
Участок цилиндра над зеркалом жидкости
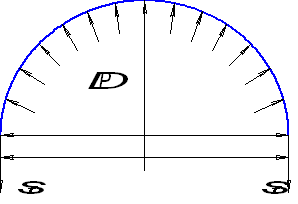
Рис. 3. Сечение II – II
Нормальным сечением к оси бака II – II отсечём часть цилиндра, расположенную над зеркалом жидкости (рис. 3). Составим уравнение равновесия для верхней отсеченной части оболочки в проекции на вертикальную ось:
![]() .
.
Отсюда меридиональное напряжение:
![]() Па.
Па.
Для цилиндра ![]() ;
; ![]() , поэтому из уравнения Лапласа получаем кольцевое напряжение:
, поэтому из уравнения Лапласа получаем кольцевое напряжение:
![]() Па.
Па.
Участок цилиндра под зеркалом жидкости
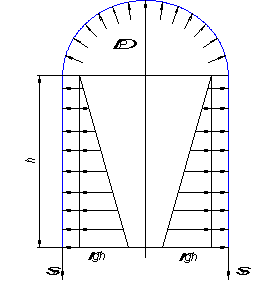
Рис. 4. Сечение III – III
Для сечения III – III расчётная схема (рис. 4) будет отличаться от показанной на рис. 3 тем, что здесь необходимо дополнительно учесть давление на стенку цилиндрической части бака со стороны жидкости.
Уравнение равновесия в проекции на вертикальную ось бака остаётся без изменений:
![]() .
.
Поэтому меридиональное напряжение не меняется:
![]() Па.
Па.
Окружное напряжение определяем из уравнения Лапласа
![]() ,
,
где ![]() Па.
Па.
Отсюда ![]() Па.
Па.
Участок нижнего полусферического днища
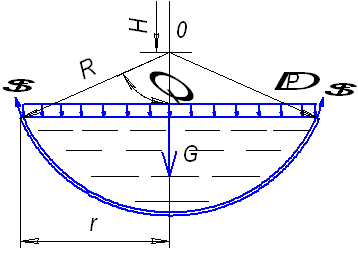
Рис. 5. Сечение IV – IV
Для нижнего днища нормальным коническим сечением IV – IV с углом ![]() при вершине отсечём нижнюю часть сферической оболочки (рис. 5). Составим для неё уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось оболочки:
при вершине отсечём нижнюю часть сферической оболочки (рис. 5). Составим для неё уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось оболочки:
![]() ,
,
где r – радиус кольцевого сечения оболочки, ![]() ;
;
S – площадь поперечного сечения, ![]() ;
;
![]() - давление в расчётном сечении оболочки,
- давление в расчётном сечении оболочки, ![]() ;
;
G – вес жидкости в объёме шарового сегмента, ![]() ;
;
Vc – объём шарового сегмента, ![]() .
.
Подставляя значения r, S, ![]() , G в уравнение равновесия определяем меридиональное напряжение
, G в уравнение равновесия определяем меридиональное напряжение ![]() :
:
![]()
Уравнение Лапласа для сферической оболочки имеет вид:
![]() .
.
Подставляя в уравнение Лапласа ![]() , находим кольцевое напряжение
, находим кольцевое напряжение ![]() в сечении IV – IV:
в сечении IV – IV:
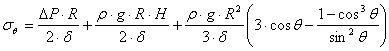 .
.
Построим таблицу 2 значений ![]() и
и ![]() в зависимости от угла
в зависимости от угла ![]() в диапазоне от 0˚ до 90˚ с шагом в 15˚:
в диапазоне от 0˚ до 90˚ с шагом в 15˚:
Таблица 2
|
|
|
|
| 0 |
|
|
| 15 |
|
|
| 30 |
|
|
| 45 |
|
|
| 60 |
|
|
| 75 |
|
|
| 90 |
|
|
По полученным напряжениям в характерных сечениях бака строим эпюры напряжений ![]() и
и ![]() (рис. 6).
(рис. 6).
Определение толщины стенок бака
Для определения толщины днищ и обечайки бака используем следующее условие:
σmax ≤ [σ], где [σ] = ![]() Па
Па
Толщина стенки ![]() .
.
Получаем: для верхнего днища ![]() м;
м;
для обечайки бака ![]() м;
м;
для нижнего днища ![]() м.
м.
Из расчётов видно, что δmax = δ2 = 0,518 мм – окончательная толщина стенки бака. По расчётной толщине стенки подбираем толщину листа согласно ГОСТ 22178 – 76:
![]() .
.
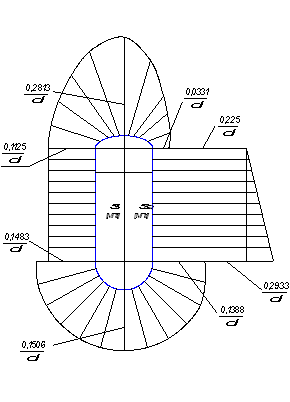
Рис.6. Эпюры безмоментных напряжений ![]() и
и ![]()
Список литературы
1. Расчёт безмоментных оболочек: Методические указания по дисциплине “Основы расчёта оболочек” для специальностей: 130600-Ракетостроение, 130400-Ракетные двигатели/ Сост. Л.И. Гречух, И. Н. Гречух.- Омск: Изд-во ОмГТУ, 2002.- 32 с.
Похожие работы
... вызывают напряжения, равномерно распределенные по ее толщине, которые принято называть цепными. Поперечная нагрузка вызывает появление напряжений изгиба, распределенных по толщине пластин по линейному закону. Подавляющее большинство пластин судового корпуса имеет прямоугольную форму опорного контура. Если одна из сторон этого опорного контура значительно больше другой, пластины будут изгибаться ...
... L L0 h hкэ hпп роп рж рцр роцр рн H1 H2 Pоп Рпл 2700 750 440 1200 2590 1.00 1.2 1.83 1.48 0.84 680 1580 12,5 26,7 Для качественного крепления обсадной колонны выбираем портландцемент ПЦТ-100, процесс цементирования производится в одну ступень. Определяем водоцементное отношение для облегченного цементного раствора и для цементного раствора по формуле: ...
... начальная сила пружины: б) уточняется сила пружины конечная: Расхождение расчётных сил и с исходными не должно быть более ± 5 ÷ ±10 %. 16 ПРОЕКТИРОВАНИЕ ДУГОГАСИТЕЛЬНЫХ УСТРОЙСТВ 16.1 Общие положения При проектировании ДУ необходимо учитывать ряд требований: 1 ДУ должно обеспечивать заданную коммутационную отключающую и включающую способность аппарата при заданных условиях ...
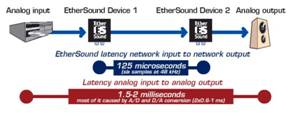
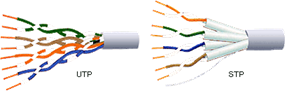
... этому представлен данный дипломный проект, который является первым в своем роде в г. Астрахани. В данном дипломном проекте рассматривается проблема построения локальной корпоративной сети звукового обеспечения интеллектуального здания на основе технологии Fast Ethernet для Областного центра детского и юношеского творчества г. Астрахани. Целью дипломного проекта является организация локальной ...



0 комментариев