Проектный расчёт червячной передачи

3.3 Проектный расчёт червячной передачи

 

Определяем межосевое расстояние:

a_w = 61(Т₂×10³/[s]²_Н)^1/3 = 61×(294×10³/189,1²)^1/3 = 123,11 мм.

Полученное значение округляем до ближайшего большего стандартного значения межосевого расстояния для червячной передачи a_w = 125 мм.

Число витков червяка z₁ = 2. Число зубьев колеса z₂ = z₁u = 2×20 = 40. Округляем до целого числа z₂ = 40.

Определим модуль зацепления

m = (1,5…1,7)a_w/z₂ = (1,5…1,7)×125/40 = 4,69…5,31 мм,

округляем в большую сторону до стандартного значения m = 5 мм.

Определяем коэффициент диаметра червяка:

q = (0,212…0,25)z₂ = (0,212…0,25)×40 = 8,48…10,00;

округляем в большую сторону до стандартного значения q = 10.

Коэффициент смещения инструмента

х = (a_w/m) – 0,5(q + z₂) = 0,00.

Определим фактическое передаточное число и проверим его отклонение от заданного:

u_ф = z₂/z₁ = 40/2 = 20,00;

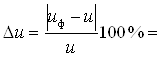(|20,00 – 20|/20)×100% = 0,00 < 4%.

Определим фактическое значение межосевого расстояния

a_w = 0,5m(q + z₂ + 2x) = 0,5×5×(10 + 40 + 2×0,00) = 125,00 мм.

Вычисляем основные геометрические размеры червяка:

делительный диаметр

d₁ = qm = 10×5 = 50,0 мм;

начальный диаметр

d_w1 = m(q + 2x) = 5×(10 + 2×0,00) = 50,0 мм;

диаметр вершин витков

d_a1 = d₁ + 2m = 50,0 + 2×5 = 60,0 мм;

диаметр впадин витков

 

d_f1 = d₁ – 2,4m = 50,0 – 2,4×5 = 38,0 мм;

делительный угол подъема линии витков

g = arctg(z₁/q) = arctg(2/10) = 11,31°;

длина нарезаемой части червяка

b₁ = (10 + 5,5|x| + z₁)m + C = (10 + 5,5|0,00| + 2)×5 + 0 = 60,0 мм,

округляем до значения из ряда нормальных размеров b₁ = 60 мм.

Основные геометрические размеры венца червячного колеса:

делительный диаметр

d₂ = d_w2 = mz₂ = 5×40 = 200,0 мм;

диаметр вершин зубьев

 

d_a2 = d₂ + 2m(1 + x) = 200,0 + 2×5×(1 + 0,00) = 210,0 мм;

наибольший диаметр колеса

d_aм2 ≤ d_a2 + 6m/(z₁ + 2) = 210,0 + 6×5/(2 + 2) = 217,5 мм;

диаметр впадин зубьев

d_f2 = d₂ – 2m(1,2 – x) = 200,0 – 2×5×(1,2 – 0,00) = 188,0 мм;

ширина венца

 

b₂ = 0,355a_w = 0,355×125,00 = 44,4 мм,

округляем до значения из ряда нормальных размеров b₂ = 45 мм;

условный угол обхвата червяка венцом колеса

2d = 2×arcsin(b₂/(d_a1 – 0,5m)) = 2×arcsin(45/(60,0 – 0,5×5)) = 103°.

Определим силы в зацеплении

окружная сила на колесе, равная осевой силе на червяке

F_t2 = F_a1 = 2000T₂/d₂ = 2000×294/200,0 = 2940 Н;

окружная сила на червяке, равная осевой силе на колесе

F_t1 = F_a2 = 2000T₂/(u_фd₁) = 2000×294/(20,00×50,0) = 588 Н;

радиальная сила, раздвигающая червяк и колесо

F_r = F_t2tg20° = 2940×0,364 = 1070 Н.

3.4 Проверочный расчёт червячной передачи

 

Фактическая скорость скольжения

v_S = u_фw₂d₁/(2cosg×10³) = 20,00×7,51×50,0/(2×cos11,31°×10³) = 3,83 м/с.

Определим коэффициент полезного действия передачи

h = tgg/tg(g + j) = tg11,31°/tg(11,31 + 2)° = 0,85,

где j – угол трения, зависящий от фактической скорости скольжения, град [1, таблица 4.9].

Проверим контактные напряжения зубьев колеса

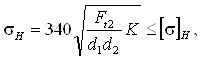
где K – коэффициент нагрузки;

[s]_Н – допускаемое контактное напряжение зубьев колеса, уточненное по фактической скорости скольжения, Н/мм² [1, таблица 3.6]

s_H = 340×(2940×1/(50,0×200,0))^1/2 = 184,4 ≤ 198,6 Н/мм².

Полученное значение контактного напряжения меньше допустимого на 7,2%, условие выполнено. Проверим напряжения изгиба зубьев колеса

s_F = 0,7Y_F2F_t2K/(b₂m) ≤ [s]_F,

где Y_F2 – коэффициент формы зуба колеса, который определяется по [1, таблица 4.10] в зависимости от эквивалентного числа зубьев колеса:

z_v2 = z₂/cos³g = 40/cos³11,31° = 42,

тогда напряжения изгиба равны

s_F = 0,7×1,53×2940×1/(45×5) = 14,0 ≤ 43,9 Н/мм²,

условие выполнено.