Тихоходный вал

6.2 Тихоходный вал

Шпонка под червячное колесо призматическая со скругленными краями по ГОСТ 23360-78: сечение 14´9, длина 56 мм, диаметр вала d = 48 мм.

Определяем напряжение смятия

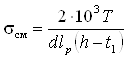= 2∙10³∙294/(48∙42∙(9 – 5,5)) = 83 МПа.

Полученное значение не превышает допустимого [s]_см = 100 МПа.

Шпонка под звездочку призматическая со скругленными краями по ГОСТ 23360-78: сечение 10´8, длина 40 мм, диаметр вала d = 35 мм.

Определяем напряжение смятия

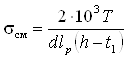= 2∙10³∙294/(35∙30∙(8 – 5)) = 97 МПа.

Полученное значение не превышает допустимого [s]_см = 100 МПа.

7. Проверочный расчет быстроходного вала

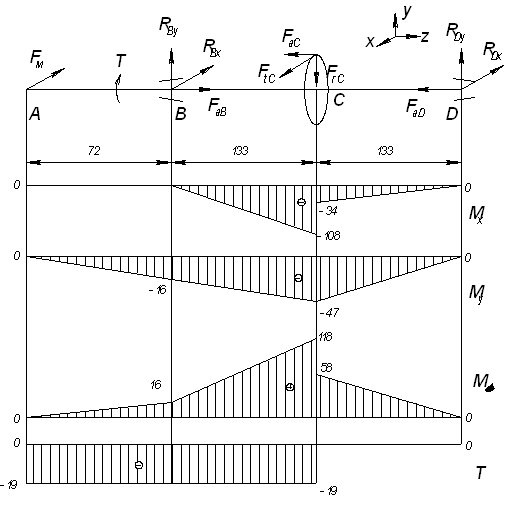
Силы, действующие на вал: F_tС = 588 Н; F_rС = 1070 Н; F_aС = 2940 Н; F_м = 50∙Т^1/2 = 50∙19^1/2 = 218 Н – консольная сила муфты.

Неизвестные реакции в подшипниках найдем, решая уравнения моментов относительно опор:

SМ_В(x) = 0;

SМ_В(x) = F_aC∙d_C/2 – F_rC∙l_BC + R_Dy∙(l_BC + l_CD) = 0;

R_Dy = (– F_aC∙d_C/2 + F_rC∙l_BC)/(l_BC + l_CD) = (– 2940∙0,050/2 + 1070∙0,133)/(0,133 + 0,133) = 259 Н.

SМ_В(y) = 0;

SМ_В(y) = – F_м∙l_AB – F_tC∙l_BC + R_Dx∙(l_BC + l_CD) = 0;

R_Dx = (F_м∙l_AB + F_tC∙l_BC)/(l_BC + l_CD) = (218∙0,072 + 588∙0,133)/(0,133 + 0,133) = 353 Н.

SМ_D(x) = 0;

SМ_D(x) = – R_Вy∙(l_BC + l_CD) + F_aC∙d_C/2 + F_rС∙l_CD = 0;

R_Вy = (F_aC∙d_C/2 + F_rС∙l_CD)/(l_BC + l_CD) = (2940∙0,050/2 + 1070∙0,133)/(0,133 + 0,133) = 811 Н.

SМ_D(y) = 0;

SМ_D(y) = – F_м∙( l_АВ + l_BC + l_CD) – R_Вx∙(l_BC + l_CD) + F_tC∙l_CD = 0;

R_Вx = (– F_м∙( l_АВ + l_BC + l_CD) + F_tC∙l_CD)/(l_BC + l_CD) = (– 218∙(0,072 + 0,133 + 0,133) + 588∙0,133)/(0,133 + 0,133) = 17 Н.

Построение эпюр:

 

Участок АВ: 0 ≤ z ≤ 0,072;

M_x(z) = 0; M_x(0) = 0 Н∙м; M_x(0,072) = 0 Н∙м.

M_y(z) = F_оп∙z; M_y(0) = 0 Н∙м; M_y(0,072) = 218∙0,072 = -16 Н∙м.

T = -19 Н∙м на всем участке.

M_S(0) = (М²_х + М²_у)^1/2.

M_S(0) = 0 Н∙м; M_S(0,072) = (0² + -16²)^1/2 = 16 Н∙м.

Участок ВС: 0 ≤ z ≤ 0,133;

M_x(z) = – R_Вy∙z; M_x(0) = 0 Н∙м; M_x(0,133) = – 811∙0,133 = -108 Н∙м.

M_y(z) = F_оп∙(l_AB + z) – R_Вх∙z;

M_y(0) = 218∙0,072 = -16 Н∙м;

M_y(0,133) = 218∙(0,072 + 0,133) – 17∙0,133 = -47 Н∙м.

T = -19 Н∙м на всем участке.

M_S(0) = (0² + -16²)^1/2 = 16 Н∙м; M_S(0,133) = (-108² + -47²)^1/2 = 118 Н∙м.

Участок CD: 0 ≤ z ≤ 0,133;

M_x(z) = – R_Вy∙(l_BC + z) + F_aC∙d_C/2 + F_rС∙z;

M_x(0) = – 811∙0,133 + 2940∙0,050/2 = -34 Н∙м;

M_x(0,133) = – 811∙(0,133 + 0,133) + 2940∙0,050/2 + 1070∙0,133 = 0 Н∙м.

M_y(z) = F_оп∙(l_AB + l_BC + z) – R_Bх∙(l_BC + z) + F_tC∙z;

M_y(0) = 218∙(0,072 + 0,133) – 17∙0,133 = -47 Н∙м;

M_y(0,133) = 218∙(0,072 + 0,133 + 0,133) – 17∙(0,133 + 0,133) + 588∙0,133 = 0 Н∙м.

T = 0 Н∙м на всем участке.

M_S(0) = (-34² + -47²)^1/2 = 58 Н∙м; M_S(0,133) = 0 Н∙м.

Проверим сечение В на запас прочности. Концентратор напряжений – переход с галтелью. Коэффициент запаса прочности:

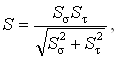
где S_s – коэффициент запаса прочности по нормальным напряжениям;

S_t – коэффициент запаса прочности по касательным напряжениям.

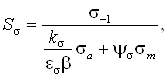
где s_-1 – предел выносливости стали при симметричном цикле изгиба, МПа;

k_s – эффективный коэффициент концентрации нормальных напряжений;

e_s – масштабный фактор для нормальных напряжений;

b – коэффициент, учитывающий влияние шероховатости поверхности;

s_a – амплитуда цикла нормальных напряжений равная суммарному напряжению изгиба s_и в рассматриваемом сечении;

y_s – коэффициент, зависящий от марки стали;

s_m – среднее напряжение цикла нормальных напряжений.

s_a = s_и = 10³М/W,

где М – суммарный изгибающий момент в сечении, Н∙м;

W – момент сопротивления сечения при изгибе, мм³.

W = pd³/32 = 3,14∙30³/32 = 2649 мм³,

s_a = s_и = 10³∙16/2649 = 5,92 МПа,

s_m = 4F_a/(pd²) = 4∙2940/(3,14∙30²) = 4161 МПа.

S_s = 410/(1,9∙5,92/(0,73∙0,94) + 0,27∙4161) = 2,36.

где t_-1 – предел выносливости стали при симметричном цикле кручения, МПа;

k_t – эффективный коэффициент концентрации касательных напряжений;

e_t – масштабный фактор для касательных напряжений;

t_a – амплитуда цикла касательных напряжений;

y_t – коэффициент, зависящий от марки стали;

t_m – среднее напряжение цикла касательных напряжений.

t_a = t_m = 0,5∙10³T/W_к,

где Т – крутящий момент в сечении, Н∙м;

W_к – момент сопротивления сечения при кручении, мм³.

W_к = pd³/16 = 3,14∙30³/16= 5299 мм³,

t_a = t_m = 0,5∙10³∙19/5299 = 1,79 МПа.

S_t = 240/(1,74∙1,79/(0,73∙0,94) + 0,1∙1,79) = 50,79.

S = 2,36∙50,79/(2,36² + 50,79²)^1/2 = 2,36.

Полученное значение находится в допускаемом интервале 1,5 – 2,5.

Проверим сечение С на запас прочности. Концентратор напряжений – переход с галтелью. Коэффициент запаса прочности:

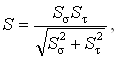
где S_s – коэффициент запаса прочности по нормальным напряжениям;

S_t – коэффициент запаса прочности по касательным напряжениям.

где s_-1 – предел выносливости стали при симметричном цикле изгиба, МПа; k_s – эффективный коэффициент концентрации нормальных напряжений; e_s – масштабный фактор для нормальных напряжений; b – коэффициент, учитывающий влияние шероховатости поверхности; s_a – амплитуда цикла нормальных напряжений равная суммарному напряжению изгиба s_и в рассматриваемом сечении; y_s – коэффициент, зависящий от марки стали; s_m – среднее напряжение цикла нормальных напряжений.

s_a = s_и = 10³М/W,

где М – суммарный изгибающий момент в сечении, Н∙м;

W – момент сопротивления сечения при изгибе, мм³.

W = pd³/32 = 3,14∙36³/32 = 4578 мм³,

s_a = s_и = 10³∙118/4578 = 25,77 МПа,

s_m = 4F_a/(pd²) = 4∙2940/(3,14∙36²) = 2890 МПа.

S_s = 410/(1,9∙25,77/(0,73∙0,94) + 0,27∙2890) = 2,47.

где t_-1 – предел выносливости стали при симметричном цикле кручения, МПа; k_t – эффективный коэффициент концентрации касательных напряжений; e_t – масштабный фактор для касательных напряжений; t_a – амплитуда цикла касательных напряжений; y_t – коэффициент, зависящий от марки стали; t_m – среднее напряжение цикла касательных напряжений.

t_a = t_m = 0,5∙10³T/W_к,

где Т – крутящий момент в сечении, Н∙м;

W_к – момент сопротивления сечения при кручении, мм³.

W_к = pd³/16 = 3,14∙36³/16= 9156 мм³,

t_a = t_m = 0,5∙10³∙19/9156 = 1,04 МПа.

S_t = 240/(1,74∙1,04/(0,73∙0,94) + 0,1∙1,04) = 87,76.

S = 2,47∙87,76/(2,47² + 87,76²)^1/2 = 2,47.

Полученное значение находится в допускаемом интервале 1,5 – 2,5.