Навигация
Определение опорных реакций и построение эпюр поперечной силы и изгибающего момента
1. Определение опорных реакций и построение эпюр поперечной силы и изгибающего момента.
ΣmB=0
RA4a + 1,5qa2 – q4a2а- 1,5qa·a = 0
RA = 2qa
ΣYi=0
RA - 4qa + 1,5qa + RB = 0
RB =0,5qa
Эпюра Qy. Поперечная сила изменяется на всех участках по линейному и принимает в характерных точках следующие значения (рис. 11,б)
QA=RA=2qa
QAD=QA – qa=2qa – qa=qa
QDB=QAD –q3a=qa – 3qa= – 2qa
QB=QDB + RB = – 2qa + 0,5qa= – 1,5qa
QBC =QB = – 1,5qa
QC=QDC + 1,5qa = – 1,5qa +1,5qa = 0
Эпюра Mx. Изгибающий момент изменяется по квадратичному закону на участке AB (q=const) и по линейному закону – на участке BC (q=0). Вычисляем значения в характерных точках и строим эпюру (рис. 11,в)
MA = 0
MAD = MA + 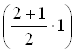 qa2 = 0+ 1,5qa2 = 1,5qa2
qa2 = 0+ 1,5qa2 = 1,5qa2
MD = MAD + 1,5qa2 = 1,5qa2+ 1,5qa2 = 3qa2
ME = MD +  qa2 = 3qa2+ 0,5qa2 = 3,5qa2
qa2 = 3qa2+ 0,5qa2 = 3,5qa2
MB = ME –  qa2 = 3,5qa2 – 2qa2 = 1,5qa2
qa2 = 3,5qa2 – 2qa2 = 1,5qa2
MC = MB – 1,5qa2 = 1,5qa2 – 1,5qa2 = 0
Расчетный изгибающий момент равен
Mрас = |ME| = 3,5qa2 = 3,5·15·103·1,22 = 75,6 кН·м
Определение перемещений.
Для перемещения упругих перемещений в инженерной практике применяются как аналитические (точные и приближенные), так и графические методы. Из точных аналитических методов следует отметить метод начальных параметров и энергетический метод. К приближенным относят метод конечных разностей (МКР) и метод конечных элементов (МКЭ).
Определим первыми двумя методами.
Метод начальных параметров.
Из граничных условий задачи имеем: νA = 0, νB = 0. Первое дает ν0 = 0, а из второго находим θ0 :
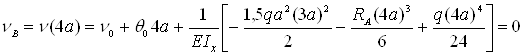
откуда

А теперь находим искомые перемещения:
– сечение z=a
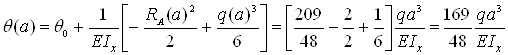
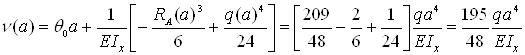
– сечение z=2a
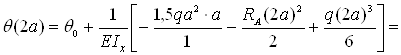
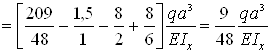
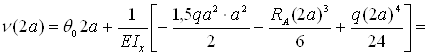
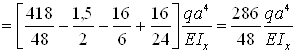
– сечение z=3a
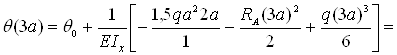
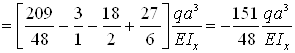
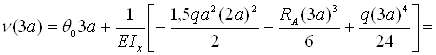
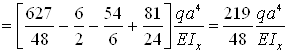
– сечение z=4a
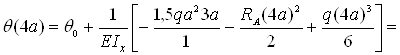
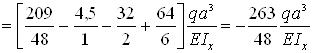
![]()
– сечение z=5a
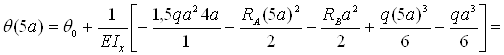
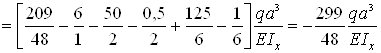
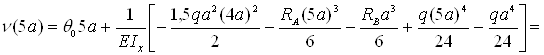
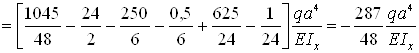
Результаты вычислений сведем в табл. 6 и построим упругую линию балки, показано на рис. 11,а пунктиром.
Таблица 6 – Перемещения и угол поворота в сечение балки
| Перемещения | Сечение z | |||||
| 0 | а | 2а | 3а | 4а | 5а | |
| θ´ |
|
|
|
|
|
|
| ν´ | 0 |
|
|
| 0 |
|
Для расчета балки на жесткость необходимо знать максимальный прогиб, который имеет место в сечении, где угол поворота равен нулю. Последний описывает полиномом 3-й степени и в связи с этим нахождение максимального прогиба связано с громоздкими вычислениями. С другой стороны, судя по приведенной выше таблице, он имеет место в интервале (2а, 3а). В силу непрерывности функции прогибов νmax мало отличается от прогиба сечения E. Следовательно, с небольшой погрешность (не превышающей точности инженерных расчетов) можно принять
νmax ≈ νЕ =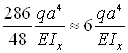
Энергетический метод
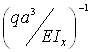
Искомые перемещения находятся с помощью интеграла Мора
![]()
для вычисления которых в простых случаях можно пользоваться правилом Верещагина
![]()
а в более сложных случаях – формулой Симпсона
![]()
При наличие на данном участке равномерно распределенной погонной нагрузки q величина момента посредине участка находится следующим образом
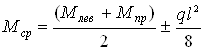
Величина моментов Млев и Мпр берутся со своими знаками. Знак «плюс» перед вторым слагаемым соответствует погонной нагрузке, направленной вниз, а «минус» – вверх.
Строим эпюры моментов от заданной нагрузки и от единичных воздействий, приложенных к балке в направлении искомых перемещений (рис. 11,г – з).
Определяем моменты по средине участков
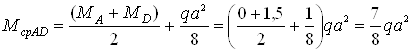
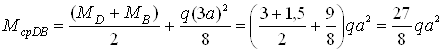
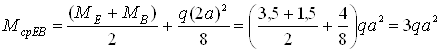
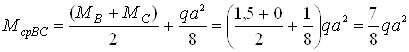
Перемножая соответствующие эпюры, находим искомые перемещения, увеличенные для удобства вычислений в EI раз:
![]()
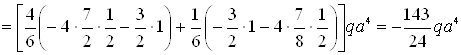
![]()
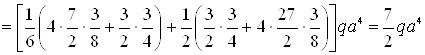
![]()
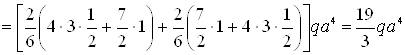
![]()
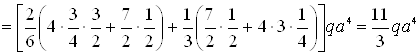
![]()
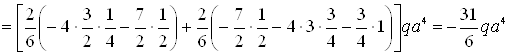
Знак «минус» у перемещения указывает, что оно противоположно направлению соответствующего единичного фактора: единичной силы для прогиба сечения С и единичного момента для угла поворота сечения В, т.е. прогиб νС направлен вверх, а сечение В поворачивается против часовой стрелки. Знак «плюс» у угла поворота θА указывает, что сечение В поворачивается в направлении единичного момента, т.е. по часовой стрелки.
Подбор сечения балки по условиям прочности и жесткости.
Из условия прочности имеем
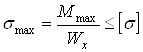
Отсюда, учитывая что
Mmax = 75,6 кН
![]()
находим диаметр сечения балки, удовлетворяющий условию прочности
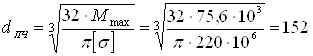 мм
мм
Далее согласно условию жесткости
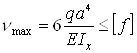
откуда с учетом
![]()
![]() мм
мм
находим искомый диаметр, удовлетворяющий условию жесткости
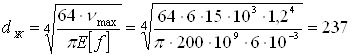 мм
мм
Из двух полученных значений принимаем большее, т.е.
d = max {dпч,dж} = dж = 237 мм
После округления до ближайшего стандартного значения по ГОСТ 6636-86 окончательно получим d0 =240 мм.
Найденное таким образом значение диаметра поперечного сечения бруса, обеспечит надежную работу балки, так как удовлетворяет одновременно и условию прочности, и условию жесткости.
Похожие работы
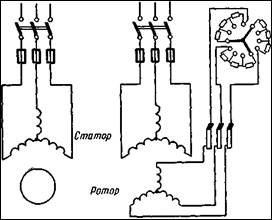
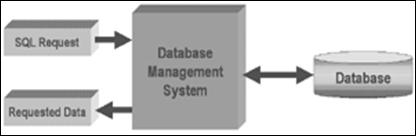
... . ЗАКЛЮЧЕНИЕ В результате работы была создана компьютерная программа «Электродвигатель», позволяющая осуществлять расчет и исследование параметров энергосберегающего асинхронного двигателя с индивидуальными номинальными данными. В процессе работы были изучены · Методология проектирования и расчета параметров асинхронного двигателя · Язык PL/SQL СУБД Oracle 8i · ...
... надежности, как и валидности, предъявляют определенные требования. Надежность и валидность можно оценить с помощью таблицы 1.1.[1] 2. РАЗРАБОТКА ПАКЕТА ТЕСТОВЫХ ЗАДАНИЙ ДЛЯ ОПЕРАТИВНОГО КОНТРОЛЯ УРОВНЯ ЗНАНИЙ СТУДЕНТОВ ПО КУРСУ «МЕХАНИКА» Одним из эффективных инструментов при проведении педагогического эксперимента является компьютерная технология оценки качества знаний, умений и навыков. ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... : мм2. Принимаем: – число сопловых отверстий. Диаметр сопла форсунки: мм. Заключение В соответствии с предложенной темой дипломного проекта “Модернизация главных двигателей мощностью 440 кВт с целью повышения их технико-экономических показателей” был спроектирован дизель 6ЧНСП18/22 с учётом современных технологий в дизелестроении и показана возможность его установки на судно проекта 14891. ...







0 комментариев