Навигация
Разработка математической модели состояния воздуха в полостях пневмоцилиндра
2.4 Разработка математической модели состояния воздуха в полостях пневмоцилиндра
Математическая модель состояния воздуха описывается адиабатой:
![]() . (2.11)
. (2.11)
где р – давление в полости, МПа;
V – объем полости, м3.
Принимаем произведение ![]() пропорциональным массе воздуха в полости:
пропорциональным массе воздуха в полости:
![]() . (2.12)
. (2.12)
Для определения пропорциональности k берем 1м3 воздуха при атмосферном давлении. Тогда выражение 2.12 примет вид:
![]() .
.
Следовательно:
![]() .
.
Для разработки математической модели необходимо рассмотреть состояние воздуха в левой и правой полости.
| Левая полость | Правая полость |
|
где V01 – начальный объем полости, 1,6956·10-4м3. |
где V02 – начальный объем полости, 24,6898·10-4м3. |
| С учетом уравнения массового расхода
масса воздуха определяется по формуле: | |
|
|
|
На рисунках 12, 13 приведены S-модели состояния воздуха в левой и правой области соответственно.
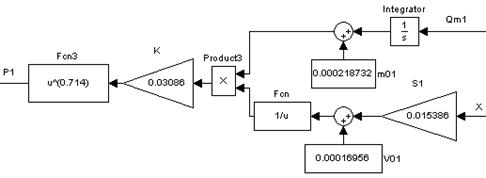
Рисунок 12 – S-модель состояния воздуха в левой полости пневмопривода
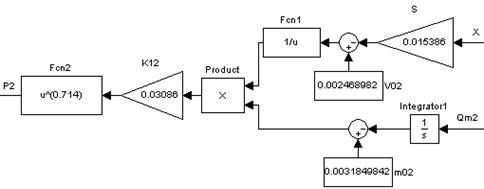
Рисунок 13 – S-модель состояния воздуха в правой полости пневмопривода
2.5 Разработка математической модели аэромеханики пневмопривода
Математическая модель аэромеханики пневмопривода выражается уравнениями гидродинамики для двух полостей. Выражение 2.13 определяет массовый расход Qm1 воздуха в левой полости, выражение 2.14 – массовый расход Qm2 в правой полости.
![]() . (2.13)
. (2.13)
![]() . (2.14)
. (2.14)
Из выражений 2.13, 2.14 видно, что входной величиной для моделей аэромеханики воздуха в полостях пневмоцилиндра является давление в соответствующих областях, а выходной – массовый расход в соответствующих областях.
На рисунках 14, 15 приведены S-модели аэромеханики соответственно для левой и правой полости.
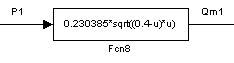
Рисунок 14 – S-модель аэромеханики в левой полости пневмопривода
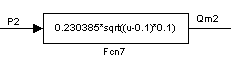
Рисунок 15– S-модель аэромеханики в правой полости пневмопривода
2.6 Разработка схемы модели пневмопривода в приложении Simulink
Рассчитанные в пунктах 2.3, 2.4 и 2.5 данной работы модели для получения общей математической модели пневмопривода следует собрать в одну систему. При разработке модели всего привода пользуемся приложением Simulink пакета программ MATLAB.
На рисунке 23 приведена общая схема S-модели пневмопривода.
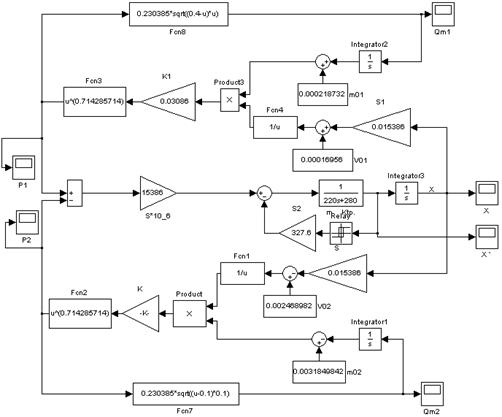
Рисунок 16 - Общая схема S-модели пневмопривода
2.7 Результаты моделирования и идентификация математической модели пневмопривода для САУ
Результаты моделирования представим в виде графиков.
На рисунке 17 приведен график зависимости перемещения поршня цилиндра от времени до достижения им крайнего правого положения (x=h=200мм).
На рисунке 18 показано изменение скорости поршня пневмоцилиндра за время движения к крайнему правому положению.
На рисунках 19, 20 отображена зависимость изменения величины давления воздуха соответственно в левой и правой полостях пневмоцилиндра.
На рисунках 21, 22 представлены графики расхода воздуха в левой и правой полостях цилиндра соответственно.
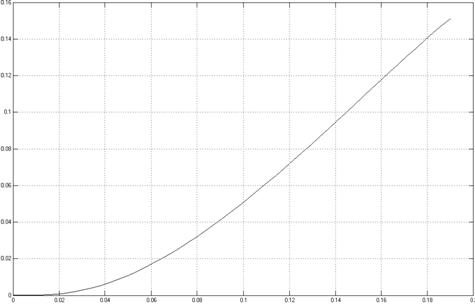
Рисунок 17 - График зависимости перемещения поршня от времени
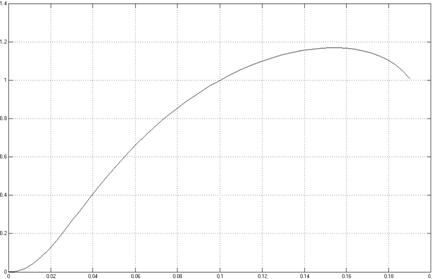
Рисунок 18 - Изменение скорости поршня пневмоцилиндра
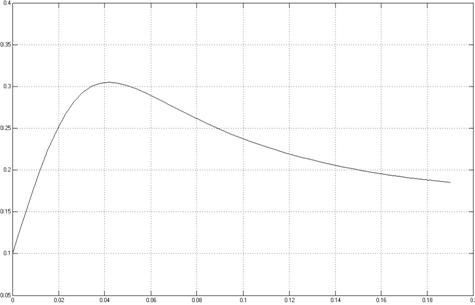
Рисунок 19- Зависимость изменения величины давления в левой полости
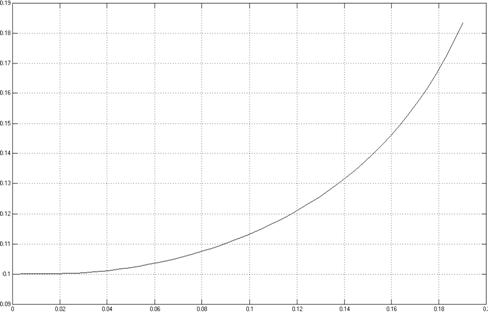
Рисунок20 - Зависимость изменения величины давления в правой полости
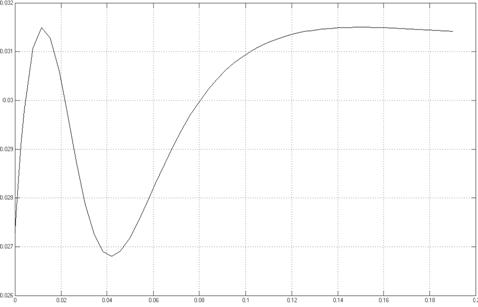
Рисунок 21 - График расхода воздуха в левой полости
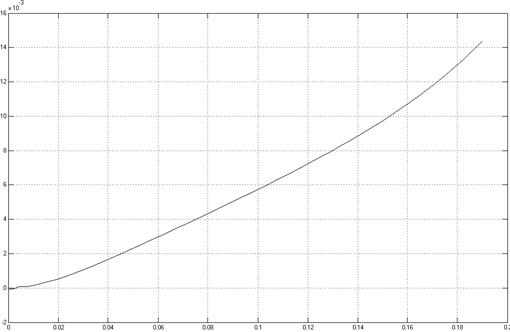
Рисунок22 - График расхода воздуха в правой полости
Идентификацию пневмоцилиндра как объекта регулирования проводим по графику перемещения поршня.
Передаточную функцию цилиндра принимаем:
![]() , (2.15)
, (2.15)
Подбираем параметры Коб и Тоб так, чтобы полученная функция наиболее точно совпадала с графиком перемещения поршня, полученным при разработке математической модели пневмоцилиндра. Воспользуемся возможностью приложения Simulink создания подсистем для уменьшения визуального представления математической модели цилиндра. На рисунке 23 представлена S-модель идентификации математической модели пневмопривода для САУ.
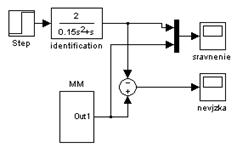
Рисунок 23 - S-модель идентификации ММ пневмопривода
Окончательно передаточная функция цилиндра принимает вид:
![]() .
.
На рисунке 24 показаны два графика математических моделей, рассчитанной и принятой в результате идентификации.
На рисунке 25 приведен график невязки двух рассматриваемых моделей. Из него следует, что полученная в результате идентификации модель может быть принята как передаточная функция объекта, так как разница между принятой и рассчитанной моделями не превышает 5% от максимального значение перемещения поршня x ![]() .
.
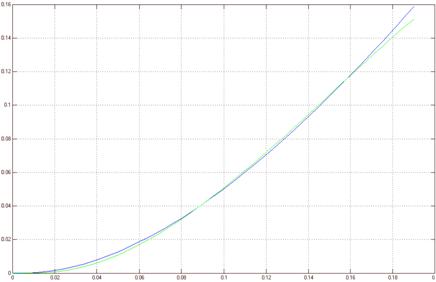
Рисунок 24 – Графики рассчитанной и принятой математических моделей
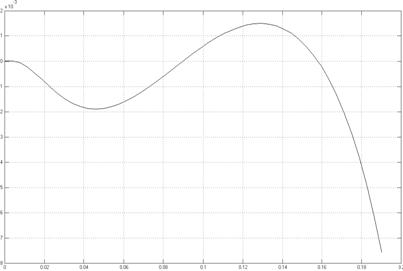
Рисунок 25 - график невязки двух рассматриваемых моделей
Для осуществления автоматического управления рассматриваемым пневмоприводом необходимо определить параметры датчиков, которые будут использованы в системе.
Для САУ пневмопривода требуются два датчика: перемещения и скорости, с коэффициентами усиления сигнала Кx и Кx` соответственно. Для их определения примем все управляющие аналоговые сигналы равными в диапазоне от –1 до +1В.
Коэффициент усиления датчика перемещения Кx определим по формуле:
![]() , (2.16)
, (2.16)
![]() .
.
![]() , (2.17)
, (2.17)
![]() .
.
Заключение
В результате выполнения данной работы была проведена разработка электромеханического привода главного движения станка 1П756ДМ и пневматического привода переключения скоростей шпинделя станка 1740РФ3, были получены математические модели вышеперечисленных систем как объектов управления САУ, рассчитаны параметры датчиков, необходимых для осуществления автоматизированного управления.
Список использованных источников
1. Металлорежущие станки /Под ред.В.Э.Пуша. --М.: Машинострое-ние, 1985.-468с.
2. Коловский М.З. Динамика машин .- Л.: Машиностроение, 1989.- 288с.
3. Решетов Д.Н., Портман В.Т. Точность металлорежущих станков.-М.: Машиностроение, 1986.-386с.
4. Ривин Е.И. Динамика приводов станков. - М.: Машиностроение, 1966.- 203 с.
5. Программа дисциплины и методические указания к выполнению курсовой работы по дисциплине "Технические средства автоматизации" для студентов специальности 2102 - Автоматизация технологических процессов и производств для студентов очной и заочной формы обучения/Кубан. гос. технол. ун-т. Сост.: Ю.Е. Кичкарь, Краснодар, 2005. - 47 с.
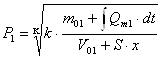 .
.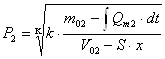 .
.
0 комментариев