Навигация
Построение модели звена второго порядка методом площадей
2.5 Построение модели звена второго порядка методом площадей
При q=1 и t=0 получаем объект второго порядка. Рассчитаем постоянные времени T1 и T2 при помощи метода площадей:
![]()
Для определения параметров передаточной функции методом площадей необходимо построить графики функций:
1) ![]()
2) ![]()
Тогда можно определить площади под графиками данных функций (S1 и S2 соответственно). Результаты вычислений представлены ниже.
S1 =
309.8824
S2 =
5.9162e+004
Графики данных функций приведены на рисунках 2.6 и 2.7 соответственно.
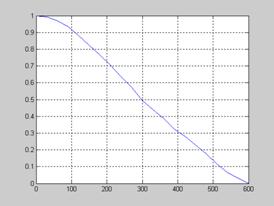
Рисунок 2.6 – График функции ![]()
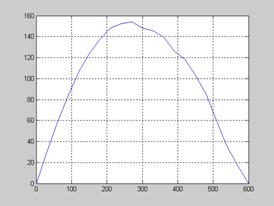
Рисунок 2.7 – График функции ![]()
Теперь необходимо проверить соотношение ![]() . Если
. Если ![]() , то метод площадей применять нельзя, необходимо использовать метод грубых площадей. В нашем случае
, то метод площадей применять нельзя, необходимо использовать метод грубых площадей. В нашем случае ![]() (полный листинг m-файла приведен в приложении В). Значит, применим метод грубых площадей.
(полный листинг m-файла приведен в приложении В). Значит, применим метод грубых площадей.
Для этого нужно найти точку перегиба графика переходного процесса. Точка перегиба имеет координаты: t = 90 c, , y(tп)=0.09.
Берем точку t правее точки перегиба (t>tп) воспользуемся формулой:
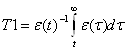 , где
, где
In=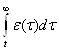 , площадь кривой после точки перегиба (пределы интегрирования: от 90(tп) до 600(¥)), причем,
, площадь кривой после точки перегиба (пределы интегрирования: от 90(tп) до 600(¥)), причем, ![]() =k*d(t), где d(t)=1-h(t), следовательно:
=k*d(t), где d(t)=1-h(t), следовательно:
![]()
Таким образом, реализуя данный алгоритм, получаем следующие результаты:
T1 =
237.2624
T2 =
72.6200
Transfer function:
514.3
---------------------------
1.723e004 s^2 + 309.9 s + 1
График переходного процесса для такого звена представлен на рисунке 2.8
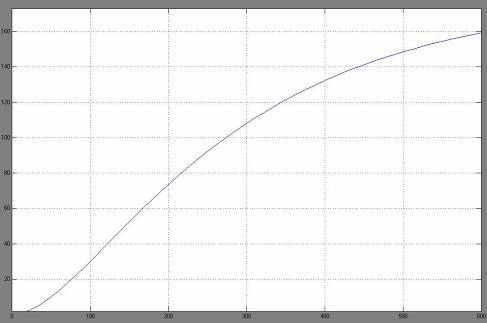
Рисунок 2.8 – График переходного процесса для звена второго порядка, рассчитанного с помощью метода площадей
2.6 Построение математической модели звена второго порядка методом Ротача
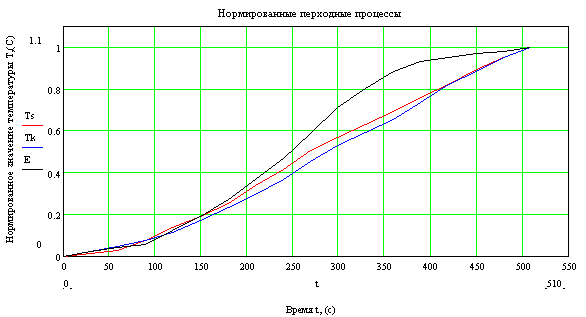
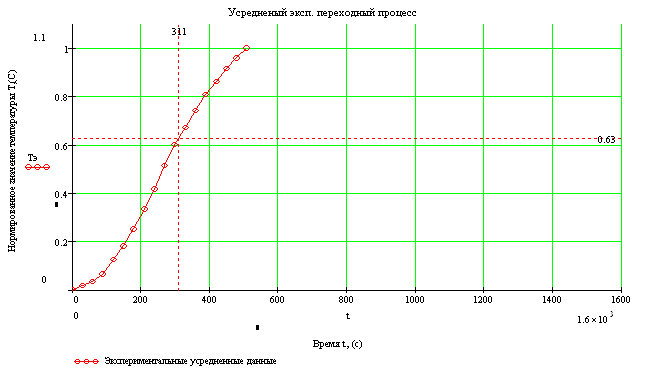
Проведем в точке перегиба касательную, для определения интервала времени Т0, заключенного между точками пересечения этой касательной оси абсцисс и линии установившегося значения h∞ переходной характеристики:
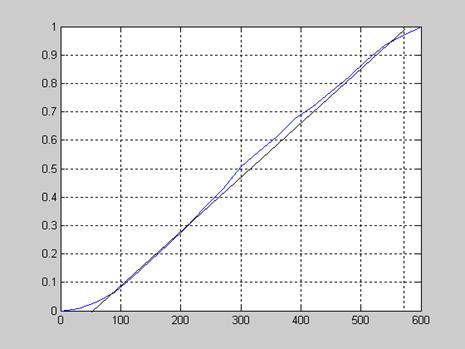
Рисунок 2.9 – Нормированный переходный процесс
Таким образом, запишем величины, являющиеся входными данными:
T0=526 tп=90, y(tп)=0,09.
Введем обозначение: ![]()
Так как ![]() , то возможна аппроксимация инерционным звеном второго порядка без запаздывания (т.е. q=1, t=0), следовательно, получаем следующую модель:
, то возможна аппроксимация инерционным звеном второго порядка без запаздывания (т.е. q=1, t=0), следовательно, получаем следующую модель:
![]()

Таким образом, запишем модель звена второго порядка без запаздывания:
![]() или
или ![]()
Теперь построим переходный процесс для данной передаточной функции.
w=tf([514.3],[8396 478.66 1]);
step(w, 600)
grid on
Результат представлен на рисунке 2.10.
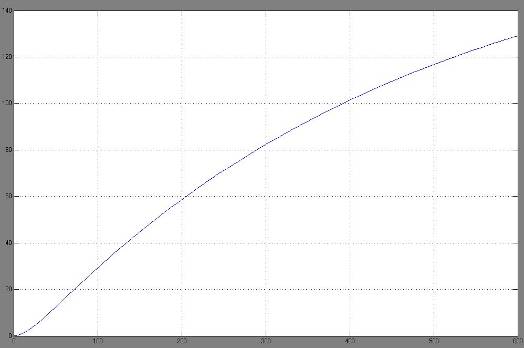
Рисунок 2.10 – График переходного процесса для звена второго порядка, рассчитанного методом Ротача
2.7 Выбор наилучшей аппроксимирующей модели
Для выбора лучшей аппроксимирующей модели объекта управления среди найденных моделей сравним теоретические и экспериментальный переходные процессы. Для оценки качества полученных передаточных функций, описывающих объект управления, вычислим оценку χ2 по формуле:
![]()
![]()
![]()
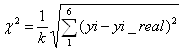
Проведенный расчет дает следующие результаты:
%Расчет погрешностей
k=514.3;
y_real=[24.44 60 93.33 125.5 154.44 180];
y1=[32 72 101 122 136 146];
y2=[31.1 73.3 106.67 131.11 148.89 160];
y3=[30 58.33 63.33 103.33 116.67 128.33];
tmp=0;
for i=1:6
tmp = tmp + (y_real(i)-y1(i))^2;
end
x1=sqrt(tmp)/k
tmp=0;
for i=1:6
tmp = tmp + (y_real(i)-y2(i))^2;
end
x2=sqrt(tmp)/k
tmp=0;
for i=1:6
tmp = tmp + (y_real(i)-y3(i))^2;
end
x3=sqrt(tmp)/k
x1 =
0.0818
x2 =
0.0571
x3 =
0.1445
x1 – соответствует оценке звена запаздывания; x2 – соответствует апериодическому звену второго порядка, рассчитанному методом площадей; x3 – соответствует апериодическому звену второго порядка, рассчитанному методом Ротача.
Так как наименьшая оценка χ2 получилась у апериодического звена второго порядка, рассчитанного интегральным методом, то это звено и возьмем в качестве модели нашей системы. Передаточная функция объекта управления имеет вид:
![]()
Похожие работы
... несчастных случаев. Рассмотрен вопрос о мероприятиях по защите окружающей среды. 7. Технико-экономическое обоснование проекта 7.1. Выбор и обоснование аналога В качестве аналога автоматизированной системы управления тепличным хозяйством выберем комплекс «АСУ «Теплица» ЗАО “НАНКО”, который реализует следующие основные функции: · регистрацию и отображение значений контролируемых ...
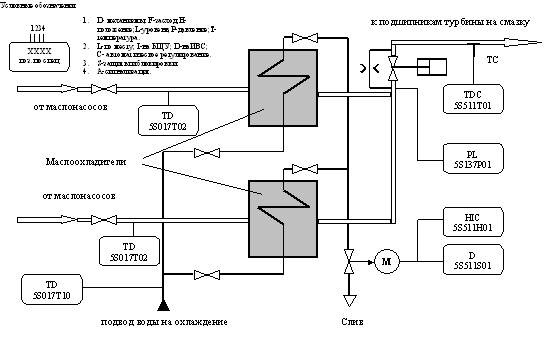
... : - по маслу 20кПа - по воде 20,1кПа Максимальное рабочее давление: - масла 0,5Мпа - воды 0,5МПа Функциональная схема системы регулирования температуры смазочного масла приведена на рис. 9. Она содержит два маслоохладителя параллельно ...
... . Алгоритм управления показывает, как должно изменяться управление u, чтобы обеспечить заданный алгоритм функционирования. Алгоритм функционирования в автоматической системе реализуется с помощью управляющих устройств. В основе используемых в техники алгоритмов управления лежат некоторые общие фундаментальные принципы управления, определяющие, как осуществляется увязка алгоритма управления с ...
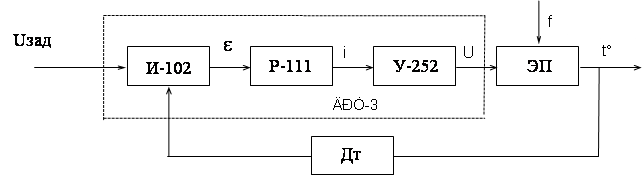
... и науки Украины Севастопольский национальный технический университет Кафедра технической кибернетики КУРСОВОЙ ПРОЕКТ по дисциплине «Системы автоматики» на тему: «Разработка и исследование системы автоматического регулирования температуры электропечи на базе промышленного регулятора Р-111» (пояснительная записка) Выполнил: ст. гр. А-41з Брусинов С.Э. Проверил: профессор ...

0 комментариев