Навигация
3 СИНТЕЗ РЕГУЛЯТОРА
3.1 Синтез регулятора методом ЛАЧХ
Для того чтобы система удовлетворяла заданным требованиям по точности и качеству (перерегулирование s ![]() 5 %, время регулирования tP
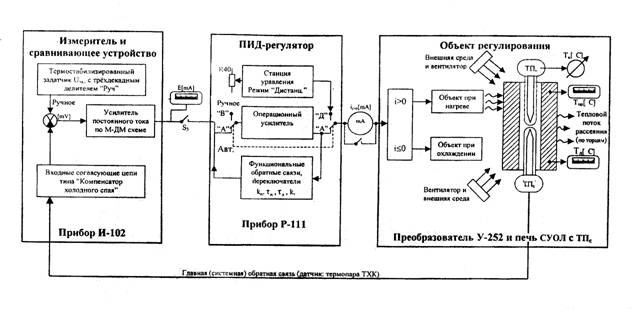
5 %, время регулирования tP![]() 420 с, коэффициент статической ошибки С0 =0), необходимо в систему, структурная схема которой изображена на рисунке 3.1, ввести регулятор.
420 с, коэффициент статической ошибки С0 =0), необходимо в систему, структурная схема которой изображена на рисунке 3.1, ввести регулятор.
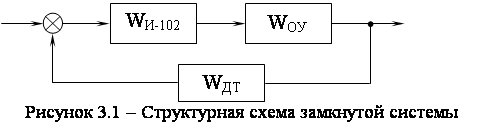
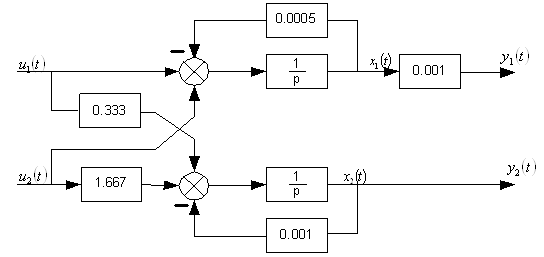
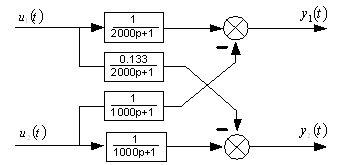
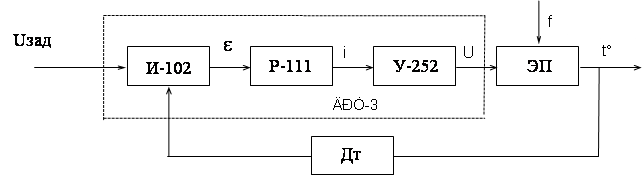
Преобразуем структурную схему, представленную на рисунке 3.1, введем в систему регулятор как корректирующее звено последовательного типа:

Рисунок 3. 2 – Структурная схема замкнутой системы с регулятором
Найдем передаточную функцию неизменяемой части прямой цепи:
![]()
где WДТ=kД – передаточная функция датчика температуры Тд;
WИ=kИ – передаточная функция измерительного блока;
WО – передаточная функция объекта управления.
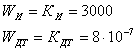
Передаточная функция прямой цепи (неизменяемой части системы):
![]()
Тогда коэффициент усиления неизменяемой части K:
![]()
Передаточная функция неизменяемой части прямой цепи будет иметь вид:
![]()
Передаточную функцию синтезируемого регулятора найдём методом логарифмических частотных характеристик. Для этого построим ЛАЧХ неизменяемой части прямой цепи исследуемой САУ:
![]()
Примем желаемую передаточную функцию в виде
![]() .
.
Желаемый коэффициент усиления определяется из соотношения:
![]() .
.
Kж=0,0186.
Передаточная функция регулятора:
![]()
Практически реализуемые регуляторы строятся с использованием следующих допущений и приближений: объект управления инерционен, и в цепях регулятора нет высокочастотных помех или они достаточно малы. Тогда высокочастотной частью регулятора можно пренебречь и считать, что T3=0. При этом желаемая ЛАЧХ рассчитывается из требования T1=T2, при желаемой ЛАЧХ в общем виде:
![]() .
.
Для определения параметров регулятора воспользуемся следующими соотношениями:
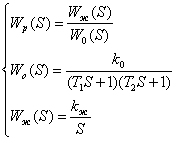
Тогда передаточная функция регулятора будет иметь следующий вид:
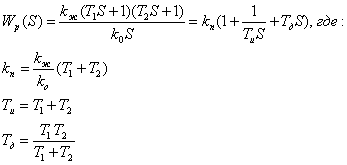
С учетом параметров объекта и звеном чистого запаздывания передаточная функция регулятора окончательно примет вид:
![]() .
.
Полученный регулятор является ПИ-регулятором с запаздыванием.
3.2 Переходная характеристика замкнутой системы
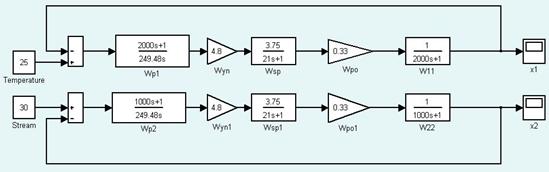
Модель построения переходной характеристики представим системе MatLab в виде передаточной функции.
Передаточная функция прямой цепи:
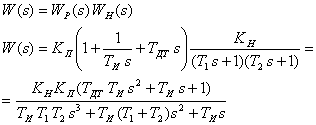
Получим передаточную функцию замкнутой системы:
![]()
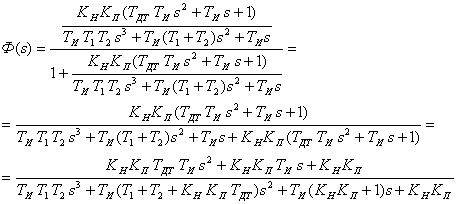
введем следующие обозначения:
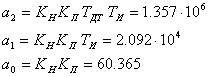
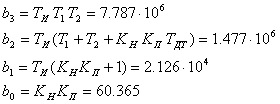
тогда передаточная функция замкнутой системы будет иметь следующий вид:
![]()
kp=4.67;
kn=1.23432;
Td=55.6;
Tu=309.8824;
T1=237.2624;
T2=72.62;
a1=kn*kp*Td*Tu
a1 =
9.9315e+004
a2=kn*kp*Tu
a2 =
1.7862e+003
b1=Tu*T1*T2
b1 =
5.3393e+006
b2=Tu*(T1+T2+kn*kp*Td)
b2 =
1.9534e+005
b3=Tu*(kn*kp+1)
b3 =
2.0961e+003
b4=kn*kp
b4 =
5.7643
a3=kn*kp
a3 =
5.7643
W=tf([a1 a2 a3],[b1 b2 b3 b4])
Transfer function:
9.932e004 s^2 + 1786 s + 5.764
----------------------------------------------
5.339e006 s^3 + 1.953e005 s^2 + 2096 s + 5.764
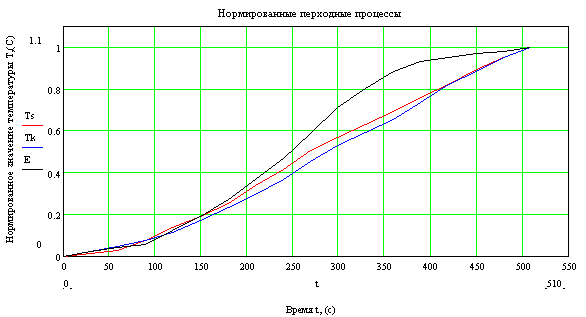
Переходный процесс для такой передаточной функции замкнутой системы представлен на рисунке 3.3.
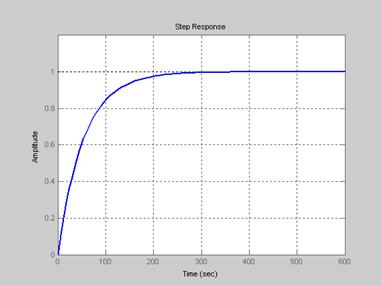
Рисунок 3.3 – График переходного процесса замкнутой системы
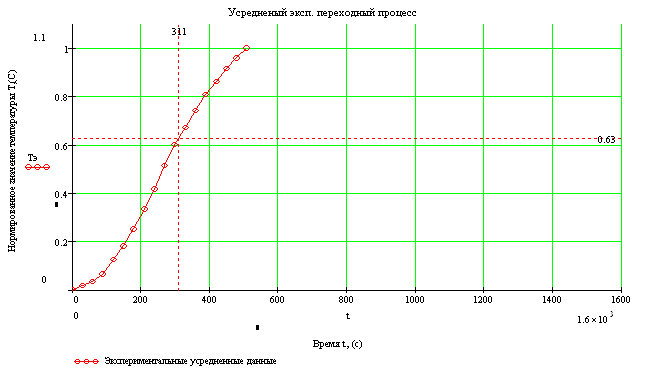
Экспериментальные данные, полученные в ходе проверки спроектированного регулятора на стенде, представлены в приложении. График переходного процесса представлен на рисунке 3.4.
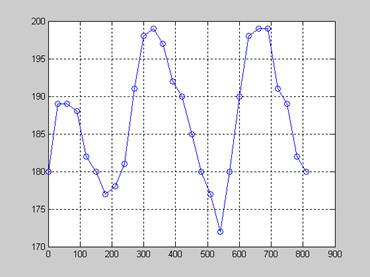
Рисунок 3.4 – График экспериментального переходного процесса замкнутой системы
Рабочая температура по варианту задания соответствует 180°C. Как видно из рисунка 3.4 все значения температуры лежат 10% коридоре, что является допустимым.
На рисунке 3.5 показан график поведения системы и установления температуры к заданному значению после действия на систему возмущения.
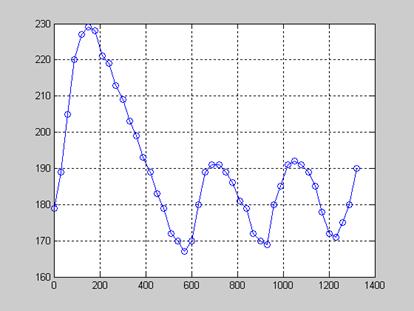
Рисунок 3.5 – График переходного процесса замкнутой системы при действии возмущающего воздействия
Из рисунка 3.5 видно, что система стабилизируется за 400 секунд, что соответствует требованиям технического задания.
ЗАКЛЮЧЕНИЕ
В ходе проектирования по экспериментальным данным была определена передаточная функция объекта. Передаточная функция определялась 3 различными способами. Причем одна передаточная функция была получена для апериодического звена первого порядка, два оставшихся метода позволяют определить параметры апериодического звена второго порядка. Именно такая передаточная функция наиболее точно описывает реальный объект.
По полученной передаточной функции был рассчитан ПИД-регулятор. Полученные параметры регулятора были, выставлены на стенде и проведены соответствующие экспериментальные исследования. Система оказалась устойчива, что подтверждает правильность расчета параметров регулятора. Соответствующие графики, иллюстрирующие поведение системы, приведены на рисунках 3.4 и 3.5.
Параметры синтезированного регулятора:
kп = 4.67
Tи = 310
Tд = 55.6
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Похожие работы
... несчастных случаев. Рассмотрен вопрос о мероприятиях по защите окружающей среды. 7. Технико-экономическое обоснование проекта 7.1. Выбор и обоснование аналога В качестве аналога автоматизированной системы управления тепличным хозяйством выберем комплекс «АСУ «Теплица» ЗАО “НАНКО”, который реализует следующие основные функции: · регистрацию и отображение значений контролируемых ...
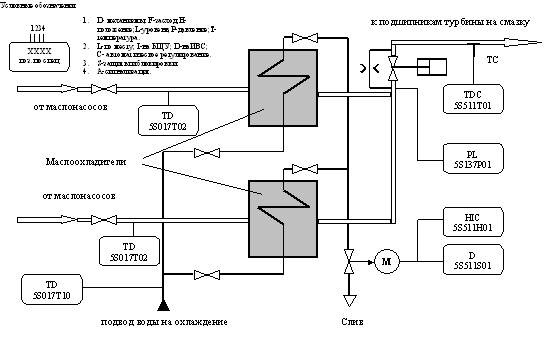
... : - по маслу 20кПа - по воде 20,1кПа Максимальное рабочее давление: - масла 0,5Мпа - воды 0,5МПа Функциональная схема системы регулирования температуры смазочного масла приведена на рис. 9. Она содержит два маслоохладителя параллельно ...
... . Алгоритм управления показывает, как должно изменяться управление u, чтобы обеспечить заданный алгоритм функционирования. Алгоритм функционирования в автоматической системе реализуется с помощью управляющих устройств. В основе используемых в техники алгоритмов управления лежат некоторые общие фундаментальные принципы управления, определяющие, как осуществляется увязка алгоритма управления с ...
... и науки Украины Севастопольский национальный технический университет Кафедра технической кибернетики КУРСОВОЙ ПРОЕКТ по дисциплине «Системы автоматики» на тему: «Разработка и исследование системы автоматического регулирования температуры электропечи на базе промышленного регулятора Р-111» (пояснительная записка) Выполнил: ст. гр. А-41з Брусинов С.Э. Проверил: профессор ...
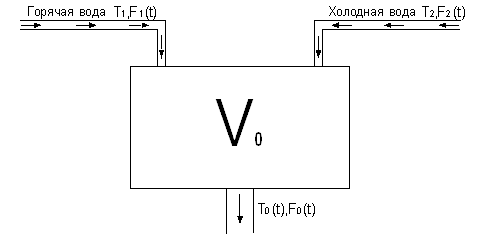

0 комментариев