Навигация
Случайные процессы в статической динамике
Предмет:
«Статистическая динамика систем автоматического управления»
Тема:
«Случайные процессы в статической динамике»
1. Случайные процессы в системах автоматического управления
Реальные системы и процессы управления могут быть представлены двумя моделями: детерминированной и статистической (вероятностной).
В детерминированных моделях структура и параметры системы являются фиксированными или детерминированными, а сигналы и процессы управления описываются детерминированными функциями и являются полностью определенными.
В статистических моделях сигналы и процессы управления, а также структура и параметры системы являются случайными величинами и описываются случайными функциями времени.
Статистическая модель является более общей и полнее описывает реальные процессы, чем детерминированные.
Статистической динамикой систем управления называется раздел теории управления, который занимается изучением динамики процесса управления в статической схеме, т. е. при случайных сигналах и динамических свойствах системы.
Статистическая динамика изучает следующие задачи:
- статистическое описание случайных процессов и динамических свойств системы;
- статистический анализ систем управления - определение статистических характеристик выходных сигналов при заданных статистических характеристиках входных сигналов и статистических свойствах системы.
- статистический синтез оптимальных систем управления - отыскание и реализация оптимальных в определенном смысле свойств системы по заданным статистическим свойствам входных сигналов.
Статистическая динамика является разделом теории управления и базируется на теории вероятности и, в частности, на ее разделе теории случайных процессов.
1.1 Основные понятия теории вероятности
Рассмотрим случайные величины и их характеристики.
Случайное событие – это событие, которое в результате опыта может произойти или не произойти (т.е. любой исход опыта).
Достоверное событие – это событие, которое в результате опыта произойдет непременно.
Невозможное событие – это событие, которое не может произойти в результате опыта.
Вероятность события - возможность появления, какого- либо события, из n –возможных событий.
Случайная величина - это численное значение случайного события.
Случайная функция – это функция, значение которой при каждом данном значении аргумента является случайной величиной.
Случайный процесс - случайная функция, аргументом которой является время.
Статистические свойства случайной величины X и случайного процесса X(t) полностью характеризуются функцией распределения вероятности F(x) (интегральным законом) или плотностью вероятности f(x) (дифференциальным законом).
1.2 Функция распределения
Функция распределения - вероятность события, которое заключается в том, что случайная величина Х примет значение меньше некоторой текущей переменной х, т.е.
F(x) = P(X<x). (1.1)
График функции распределения представлен на рис. 1.1.
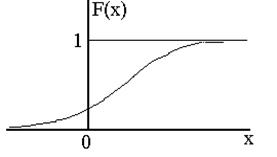
Рис. 1.1
Свойства функции распределения:
Функция распределения - возрастающая функция от 0 до 1
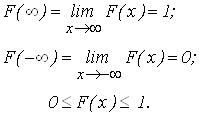 (1.2)
(1.2)
Функция распределения – неубывающая функция
![]() если
если ![]() (1.3)
(1.3)
Для любых ![]() если
если ![]() , выполняется соотношение
, выполняется соотношение
![]() (1.4)
(1.4)
1.3 Плотность вероятности
Плотность вероятности - вероятность попадания случайной величины в область x, x+Dx при Dx®0.
![]() (1.5)
(1.5)
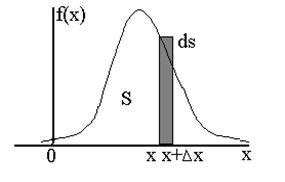 |
График плотности вероятности показан на рис. 1.2.
Рис. 1.2
Свойства плотности вероятности:
Плотность вероятности неотрицательная функция
![]() (1.6)
(1.6)
2. Площадь под кривой плотности вероятности равна единице
![]() . (1.7)
. (1.7)
3. Связь функции распределения с плотностью вероятности
![]() .(1.8)
.(1.8)
4. Вероятность попадания в область
![]() (1.9)
(1.9)
1.4 Законы распределения
Различные классы случайных событий подчинены различным законам распределения. На практике при исследовании случайных событий широко используются следующие законы распределения: нормальный, равномерный, показательный, биномиальный, Эрланга, Пуассона, Рэлея, и др.
Рассмотрим законы, наиболее часто используемые в статистической динамике систем управления.
Нормальный закон распределения (закон Гаусса). Нормальный закон распределения это закон, наиболее часто встречающийся на практике при исследовании систем управления.
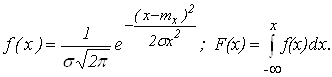 . (1.10)
. (1.10)
Плотность вероятности и функция распределения для нормального
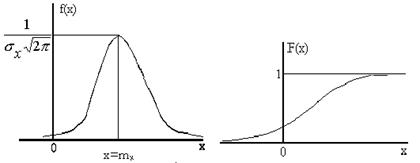 |
закона приведены на рис. 1.3а, б.
Рис.1.3. а) б)
Как видно из графика (рис. 1.3) и формулы (1.10), нормальный закон распределения случайной величины X зависит от двух параметров: математического ожидания mx и среднего квадратичного отклонения этой величины sx.
Закон равномерной плотности. Плотность вероятности и функция распределения для закона равномерной плотности приведены на рисунке 1.4.
 (1.11)
(1.11)
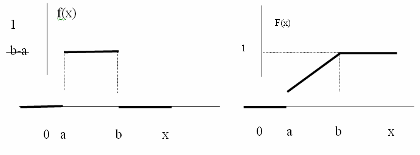
Рис.1.4
Похожие работы
... . Деятельность формирует психические процессы. Любая деятельность – это соединение внутренних и внешних поведенческих действий и операций. Мы рассмотрим каждый вид психической деятельности отдельно. 2. Психические процессы как форма деятельности Психические процессы – общее название ощущений, восприятий, приспособлений, внимания, памяти, мышления, воображения, речи. Все они участвуют в ...
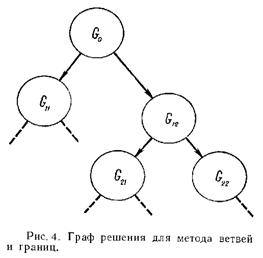
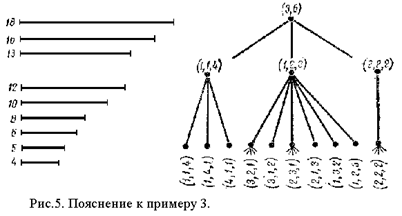
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... инструментарий исследования организационных отношений. 3.4 Заслуги А.А. Богданова в разработке организационной науки Главная заслуга российских исследователей - разработка фундаментальных методологических проблем теории организации. Одним из выдающихся ученых, внесших наиболее весомый вклад в разработку организационной науки, является А.А.Богданов (Малиновский) (1873 - 1928). Добытые и ...





0 комментариев