Навигация
Классификация случайных процессов
2.1 Классификация случайных процессов
Случайные процессы можно классифицировать: стационарные; нестационарные (стохастические);
Стационарные процессы можно классифицировать: эргодические; неэргодические.
Стохастические процессы – это процессы, для определения статистических свойств которого необходимо усреднение, как по множеству, так и по времени.
Стационарные процессы – это процессы, для определения статистических свойств которого необходимо усреднение только по множеству, так как его числовые характеристики не зависят от времени.
Эргодические процессы - процессы, в которых статистические характеристики, определенные усреднением по времени, равны характеристикам, полученным усреднением по множеству. Для определения статистических свойств такого процесса используют одну, достаточно длинную реализацию x(t) на интервале [-T, T]. При этом
 (2.3)
(2.3)
2.2 Числовые характеристики случайных процессов
Математическим ожиданием (средним значением) случайного процесса X(t) называют неслучайную функцию времени mx(t), значение которой в каждый момент времени равно математическому ожиданию соответствующего сечения случайного процесса
![]() . (2.4)
. (2.4)
При этом mx (t) представляет как бы ось симметрии отдельных реализаций, т. е. степень разбросанности относительно средней оси.
Для стационарных процессов
![]() . (2.5)
. (2.5)
Для эргодических процессов
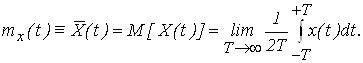 (2.6)
(2.6)
Средний квадрат случайного процесса X(t) характеризует среднюю мощность процесса и определяется по формуле:
![]() . (2.7)
. (2.7)
Для стационарных процессов
![]() . (2.8)
. (2.8)
Для эргодических процессов
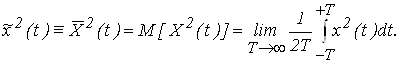 (2.9)
(2.9)
Дисперсией случайного процесса X(t) называют неслучайную функцию времени Dx(t), значение которой в каждый момент времени равно дисперсии соответствующего сечения случайного процесса
![]() . (2.10)
. (2.10)
Для стационарных процессов
 . (2.11)
. (2.11)
Для эргодических процессов
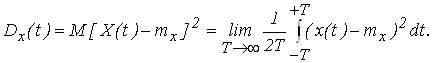 (2.12)
(2.12)
Математическое ожидание и дисперсия характеризуют процесс в отдельных сечениях, но не учитывают их взаимосвязь, эта взаимосвязь характеризуется корреляционной функцией.
Корреляционной (автокорреляционной) функцией случайного процесса X(t) называют неслучайную функцию двух аргументов Rxx(t1,t2), которая для каждой пары значений аргументов t1 и t2 равна корреляционному моменту соответствующих сечений случайного процесса
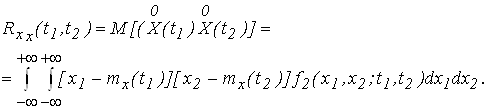 (2.13)
(2.13)
Корреляционная функция характеризует степень статистической взаимосвязи между двумя сечениями случайного процесса.
Взаимно корреляционная функция равна
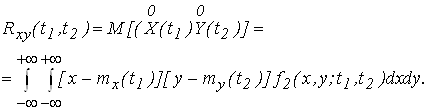 (2.14)
(2.14)
Взаимно корреляционная функция характеризует степень статистической взаимосвязи между сечениями для двух процессов.
Для Гаусcовских случайных процессов определяющей характеристикой является двумерная плотность вероятности, поэтому корреляционная функция полностью характеризуют статистические свойства случайного процесса.
Для стационарных процессов корреляционная функция зависит от разности аргументов t = t2 –t1
 (2.15)
(2.15)
При этом дисперсия равна
![]() .(2.16)
.(2.16)
Для эргодических процессов
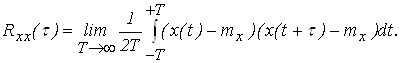 (2.17)
(2.17)
2.3 Основные свойства корреляционной функции
1. Начальное значение корреляционной функции равно дисперсии
![]() .(2.18)
.(2.18)
2. Значение Rx(t) при любом t не может превышать ее начального значения
![]() (2.19)
(2.19)
3. Корреляционная функция симметрична относительно своих аргументов
![]() (2.20)
(2.20)
![]() .
.
Для взаимно корреляционных функций это не справедливо
4. Корреляционная функция стационарных процессов является четной функцией, а взаимно корреляционная – нечетной
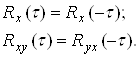 (2.21)
(2.21)
5. Корреляционная функция суммы Z(t) = X(t)+Y(t), где X(t) и Y(t) – случайные процессы
![]() (2.22)
(2.22)
6. Корреляционная функция произведения Z(t) = X(t)Y(t), где X(t)–случайный процесс, а Y(t) - неслучайная помеха
 (2.23)
(2.23)
7. Корреляционная функция суммы Z(t) = X(t)+Y(t), где X(t) – случайный процесс, а Y(t) – неслучайная функция
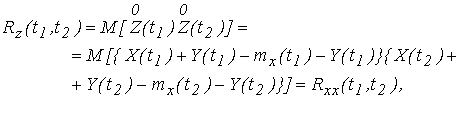 (2.24)
(2.24)
так как 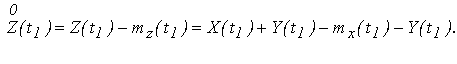
8. Для автокорреляционной функции можно записать выражение
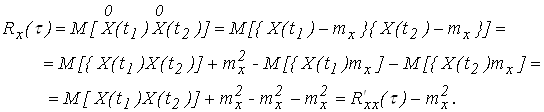
Для взаимно корреляционной функции можно записать выражение
![]() (2.26)
(2.26)
Литература
1. Бойко Н.П., Стеклов В.К. Системы автоматического управления на базе микро-ЭВМ.- К.: Тэхника,1989. –182 с.
2. Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского - М.: Высш. Шк.,1986. -312 с.
3. Гальперин М. В. Автоматическое управление Издательство: ИНФРА-М, ИЗДАТЕЛЬСКИЙ ДОМ, 2004с. – 224с.
4. Иванов В.А., Медведев В.С., Чемоданов Б.К., Ющенко А.С. Математические основы теории автоматического управления. В 3 томах. Том 1 Издательство: МГТУ им. Н.Э. БАУМАНА, 2006.
5. Справочник по теории автоматического управления. /Под ред. А.А. Красовского- М.: Наука, 1987. -712 с.
6. Теория автоматического управления: Учебник для вузов. Ч1/Под ред. А.А. Воронова- М.: Высш. Шк.,1986.-367 с.
Похожие работы
... . Деятельность формирует психические процессы. Любая деятельность – это соединение внутренних и внешних поведенческих действий и операций. Мы рассмотрим каждый вид психической деятельности отдельно. 2. Психические процессы как форма деятельности Психические процессы – общее название ощущений, восприятий, приспособлений, внимания, памяти, мышления, воображения, речи. Все они участвуют в ...
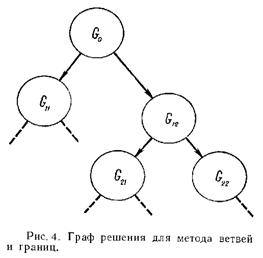
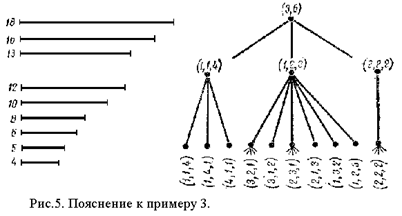
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... инструментарий исследования организационных отношений. 3.4 Заслуги А.А. Богданова в разработке организационной науки Главная заслуга российских исследователей - разработка фундаментальных методологических проблем теории организации. Одним из выдающихся ученых, внесших наиболее весомый вклад в разработку организационной науки, является А.А.Богданов (Малиновский) (1873 - 1928). Добытые и ...





0 комментариев