Навигация
Уравнения, отражающие равенство количества - ценного компонента, поступающего на операцию, количеству, выходящему с нее:;
3. Уравнения, отражающие равенство количества - ценного компонента, поступающего на операцию, количеству, выходящему с нее:;
Ха + Хз = Xi + *2 • или Хз = xl;
х4 + х5 = х3, Х6 + Х7 = Х4,
Х8 + Х9 = Хб + Х12 И Т.Д.
Легко убедиться, что общее число уравнений всех типов, которые можно составить, во много раз превышает число неизвестных, хотя система должна иметь единственное решение и соответственно число уравнений должно быть равно числу неизвестных. Причина, очевидно, состоит в том, что большая часть уравнений представляет собой линейные комбинации других; например, из
Х2 = 0,2 (Хт + Х2),
Х3 = 0,8 (Xi + Х2) следует
Ха + Хз = Xi + х2, или Хз = Xi;
Хз: Х2 = 0,8: 0,2, или Х3 = 4Х2.
В то же время решение возможно только при условии, что при числе уравнений, равном числу неизвестных, все уравнения линейно независимы. Поэтому после составления системы уравнений необходим тщательный контроль отсутствия в ней линейно зависимых (дублирующих) уравнений.
По-видимому, дублирования уравнений проще всего избежать, используя в системе, кроме уравнения, задающего производительность, только соотношения между количеством ценного компонента в потоке, выходящем с операции, и количеством, поступающим на эту операцию. Для схемы, показанной на рис.7, можно составить, например, следующую систему уравнений для определения потоков ценного компонента при производительности по конечному продукту, равной 1000:
1. Х2 = 0,2 (х-i + Х2), или Х2 = 0,25 Xi;
2. х3 = 0,8(х1 +х2);
3. х4 = о. з Хз;
4. Х5 = 0,7 Хз;
5. Хб = 0,98 Х4;
б ху = 0,02 х4;
7. х8 = 0,05 (х6 + х12);
8. Х9 = 0,95(Х6 + Х12);
э. хю = 0,01 х9;
10. Хц =0,99 Xg;
11. х12 = о,1 (хб + хц);
12. Х13 = 0,9(Х5 + Хц);
13. Х13 = 1000.
Подобную систему уравнений можно довольно легко решить вручную, путем последовательной подстановки, сокращения переменных при вычитании одних уравнений из других и т.д. Однако если число неизвестных очень велико (а в реальных схемах число потоков может достигать многих десятков и даже сотен), возрастает трудоемкость расчетов и вероятность ошибок. В подобных случаях для сокращения числа уравнений можно рекомендовать обозначать неизвестными не количества ценного компонента в каждом из потоков, а суммарные количества, поступающие на операции схемы; при этом, очевидно, число уравнений на 1 больше числа операций. Например, для той же схемы (рис.7) получаем:
1. У1 = G ucx + 0,2 /!, или 0,8 у! = G исх;
2. у2 = 0,8 yi;
3. уз = о, з у2;
4. у4 = 0,98 Уз + 0,1 Уб',
5. у5 = 0,95 у4;
6. у6 = 0,7 у2 + 0,99 у5;
7. G исх = 0,9 у6.
После решения подобной системы уравнений расчет количества ценного компонента в каждом из потоков не вызывает затруднений.
Однако наиболее эффективным способом преодоления трудностей расчета сложных технологических схем является использование компьютеров.
В отличие от человека, выбирающего для каждой конкретной системы уравнений наиболее рациональный путь решения, в программах для цифровых вычислительных машин можно использовать только универсальные, единые для всех систем линейных уравнений способы вычисления. Среди таких способов наиболее распространены метод Гаусса с выбором главного элемента столбца или строки и метод обращения матрицы [2].
До начала вычислений необходимо ввести исходные данные: при использовании метода Гаусса - расширенную матрицу коэффициентов системы линейных уравнений (значения коэффициентов при неизвестных и свободные члены каждого из уравнений):

а при использовании метода обращения матрицы - отдельно квадратную матрицу коэффициентов и вектор-столбец свободных членов:
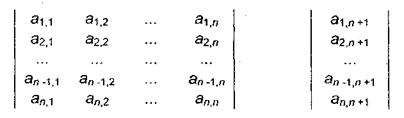
Для составления матрицы коэффициентов члены уравнений, содержащие неизвестные, необходимо расположить слева от знака равенства в порядке возрастания индекса неизвестного, оставив справа только свободные члены; отсутствующие неизвестные вносят в уравнения с коэффициентами, равными нулю. После этого можно приступить к вводу матрицы коэффициентов.
Однако применительно к системе уравнений, получаемой при описании распределения ценного компонента по потокам технологической схемы, этот способ нерационален, так как подавляющая часть коэффициентов равна нулю. Например, при вводе коэффициентов составленной ранее системы из 13 уравнений первые две строки должны быть записаны в следующем виде: - 0,25 Xi + 1 Х2 + О Х3 + О Х4 + О Х5 + О Х6 + О Х7 + О Х8 + О Х9 +
+ о х10 + о хп + ох12+ о х13 = о;
- 0,8 х1 - 0,8 х2 + 1 хЗ + 0 х4 + 0 х5 + 0 хб + 0 х7 + 0 х8 + О Х9 +
+ о Хю+ о х-и +о X-I2 + о х13 = о,
а первые две строки расширенной матрицы коэффициентов
соответственно
-0,25 1 000000000000 - 0,8 - 0,8 000000000000
При большом числе неизвестных количество вводимых нулей становится громадным: например, при 40 неизвестных расширенная матрица состоит из 40 х 41 = 1640 коэффициентов, из которых более 1500 будут равны нулю. Очевидно, что ввод подобной матрицы настолько трудоемок и неизбежно сопровождается таким количеством ошибок, что превращается в сложную задачу.
Это затруднение устраняется, если ввод матрицы осуществлять в два этапа: сначала заполнить всю матрицу нулями (эта операция выполняется очень легко), а затем ввести ненулевые коэффициенты, заменяя ими нули.
Ниже описан расчет балансов по ценному компоненту методом Гаусса с помощью программы на языке BASIC и методом обращения матрицы с помощью табличного процессора EXCEL [3, 4].
mCu(H20) 4ci2: (0,594+0,178) Mcu(mo) 4 012 206,44/165,54 = 0,963
mcocn: 7,756 M 7,756 Mc0ci2129,83/165,25= 6,093
Количество МНЦ С1, (кг/ч):
(165,765*2*53,5/249,85) +(7,756*6*53,5/165,28) +(3,683*6*53,5/244,28) +(0,963* 4*53,5/
206,44) =91,891
Количество поглощаемой реакциями H2O, (кг/ч):
(3,683*4*18/244,28) +(0,963*2*18/206,44) +(6,093*0,5*18/129,83) =1,676
Количество образующейся Н2О, (кг/ч):
7,756*3*18/165,765=2,527
Количество Н2О, приходящее с кислотой, (кг/ч):
Состав кислоты 19,8% НС1 80,2% Н2О
Количество требуемого НС1, (кг/ч):
(165,765*2*36,45/249,85) + (7,756 * 9 * 36,45 / 165,28) + (3,683 * 8 * 36,45 / 244,28) +(0,963*6*36,45/206,
44) =69,177
Приходящей с кислотой Н2О, (кг/ч):
69,177*0,802/0, 198= 280, 202
Суммарное количество приходящей Н2О, (кг/ч):
280, 202+525,985=806,187
Суммарное количество уходящей Н2О, (кг/ч):
806,187+2,527-1,676=807,03 8
Таблица 14. Материальный баланс осаждения.
| Приход | Образуется | ||||||
| |||||||
| Вещество | кг/ч | % | Вещество | кг/ч | % |
| |
| (NH4) 2 WO4 | 201,227 | 18,033 | H2W04 | 165,765 | 15,414 |
| |
| [Co(NH3) 6] (OH) 3 | 35,500 | 3,181 | Zn(H2O) 6Cl2 | 3,683 | 0,342 |
| |
| [Zn (NH3) 6] (OH) 2 | 3,036 | 0,272 | Си(Н2О) 4С12 | 0,963 | 0,090 |
| |
| [Си (NH3) 6] (OH) 2 | 0,774 | 0,069 | СоС12 | 6,093 | 0,567 |
| |
| NH4C1 | 91,891 | 8,545 |
| ||||
| НС1 | 69,177 | 6, 199 |
| ||||
| Н2О | 806,187 | 72,245 | Н20 | 807,038 | 75,043 |
| |
| Всего | 1115,901 | 100 | Всего | 1075,433 | 100 |
| |
| Невя: | ка от прихода | 40,468 | 3,626 |
| |||
WOs получают термическим разложением H2WC4 при 750-800 °С
При прокалке идет следующая реакция:
H2WO4^WO3+H2O
Количество продуктов, (кг/ч):
Масса WO3 =153,79 (кг/ч)
Масса Н2О = 165,765-153,76= 11,075 (кг/ч)
Вывод: полученная нарастающая с каждой стадией невязка до 3,626% вызвана погрешностью расчетов.
Операция №1
Переведем заданный базис из объема в массу.
m = V * ρ
m = 1000 * 1,120 = 1120т или 1120000кг.
1). G01 = 1120000
2Fe3+ + Fe → 3Fe2+
m (Fe) = mр-ра / ρр-ра * (с(Fe3+) / М(Fe2O3)) * M(Fe)
Для того, чтобы считать восстановление полным, введем 10% избыток железной стружки.
G011 = G01 / 1,120 * 0,005 /159,7 * 55,8 * 1,1 = 0,001715828 * G01
2). G011 - 0,001715828 * G01 = 0
Операция №2
3). G12 – G01 – G011 = 0
При экстракции соотношение объемов водной (сернокислый раствор) и органической (раствор 0,1 моль/л Д2ЭГФК в керосине) равно 10, т.е. Vв: Vо = 10: 1. Такое соотношение фаз берётся для большего концентрирования ценного компонента.
V = m / ρ
Vв = G12 / ρ12; Vо = G050 / ρ050
10 * ρ12 * G050 = G12 * ρ050
G050 = G12 * ρ050 / 10 * ρ12
G050 = G12 * 0,744 / 10* 1,120 = 0,0664285 * G12
4). G050 – 0,0664285 * G12 = 0
G200 = G12 - G01 / 1,120 * 0,05 (ThO2) - G01 / 1,120 * 0,2 (TiO2) - G01 / 1,120 * 0,57 (РЗЭ) - G01 / 1,120 * 0,4 (V2O5) - G01 / 1,120 * 0,02 * 0,999 (Sc2O3)
5). G200 - G12 + 0,001107125 = 0
6). G23 - G050 - G12 + G200 = 0
Операция №3
При реэкстракции примесей соотношение объемов водной (Раствор 4,5 моль/л H2SO4) и органической (Экстракт содержащий Sc, Ti, Fe3+, РЗЭ и др.) равно 1, т.е. Vв: Vо = 1: 1. Такое соотношение фаз берётся для лучшего извлечения примесей.
G030 = G23 * ρ030 / ρ23
G030 = 1,260 / 0,744 * G23 = 1,693548387 * G23
7). G030 - 1,693548387 * G23 = 0
G300 = G030 + (G01 / 1,120 * 0,05 (ThO2) + G01 / 1,120 * 0,2 (TiO2) + G01 / 1,120 * 0,57 (РЗЭ) + G01 / 1,120 * 0,4 (V2O5)) - G01 / 1,120 * 0,02 * 0,999 (Sc2O3)
8). G300 - G030 – 0,001089285 * G01
9). G34 – G030 – G23 + G300 = 0
Операция №4
При реэкстракции скандия соотношение объемов водной (Раствор 2,5 моль/л NaOH) и органической (Органическая фаза содержащая Sc) равно 0,1, т.е. Vв: Vо = 1: 10. Такое соотношение фаз берётся для большего концентрирования ценного компонента (скандия).
G040 = G34 * ρ040 / 10 * ρ34
G040 = 1,110 / 10 * 0,744 * G34 = 0,147849462 * G34
10). G040 - 0,147849462 * G34 = 0
G45 = G34 – m(Sc3+) + m(Na+)
ScA3 + 3 NaOH → Sc(OH) 3 + 3 NaA
m(Sc3+) = (G01 /1,120 * 0,02 * 0,999) / M(Sc2O3) * 2 * M(Sc(OH) 3) = (G01 /1,120 * 0,02 * 0,999) /137,91 * 2 * 95,97792 = 0,00002483 * G01
m(Na+) = (G01 /1,120 * 0,02 * 0,999) / M(Sc2O3) * 6* M(Na) = (G01 /1,120 * 0,02 * 0,999) / 137,91 * 6* 22,9897 = 0,000017842 * G01
G45 = G34 – 0,000006987 * G01
11). G45 – G34 + 0,000006987 * G01 = 0
12). G46 – G040 – G34 + G45 = 0
Операция №5
При регенерации экстрагента соотношение объемов водной (Раствор 0,5 моль/л H2SO4) и органической (Раствор Д2ЭГФК (натриевая форма)) равно 1, т.е. Vв: Vо = 1: 1.
G051 = G45 * ρ051 / * ρ45
G051 = 1,030 / 0,744 * G45 = 1,384408602 * G45
13). G051 - 1,384408602 * G45 = 0
14). G500 – G051 – G45 + G050 = 0
Операция №6
15). G600 – G46 + G67 = 0
После прохождения операции центрифугирования осадок Sc(OH) 3 имеет влажность 20%.
G67 = m(Sc(OH) 3) / 0,8
G67 = (G01 /1,120 * 0,02 * 0,999) / M(Sc2O3) * 2 * M(Sc(OH) 3) / 0,8 = (G01 /1,120 * 0,02 * 0,999) /137,91 * 2 * 95,97792 / 0,8 = 0,00002483 * G01 / 0,8 = 0,000031037 * G01
16). G67 - 0,000031037 * G01 = 0
Операция №7
G700 = G01 / M(Sc2O3) * 0,999 * 3 * M(H2O) + G67 * 0,2 = 0,000006985 * G01 + 0,2 * G67
17). G700 - 0,000006985 * G01 - 0,2 * G67
18). G70 – G67 + G700 = 0
Заменим потоки в уравнениях на соответствующие неизвестные X.
Общий вид уравнений материального баланса.
1). X1 = 1120000
2). X2 – 0,0017158280*X1 = 0
3). X3 – X1 – X2 = 0
4). X4 – 0,0664285*X3 = 0
5). X5 – X3 + 0,001107125*X1 = 0
6). X6 – X4 – X3 + X5 = 0
7). X7 – 1,693548387*X6 = 0
8). X8 – X7 – 0,001089285*X1 = 0
9). X9 – X7 – X6 + X8 = 0
10). X10 – 0,147849462*X9 = 0
11). X11 – X9 + 0,000006987*X1 = 0
12). X12 – X10 – X9 + X11 = 0
13). X13 – 1,384408602*X11 = 0
14). X14 – X13 – X11 + X4 = 0
15). X15 – X12 + X16 = 0
16). X16 – 0,000031037*X1 = 0
17). X17 – 0,000006985*X1 – 0,2*X16 = 0
18). X18 – X16 + X17 = 0
Расчет полученных уравнений материального баланса ведем с помощью табличного процессора EXCEL [15]. (см. Приложение 1).
Сводные таблицы материального баланса.
| приход | кг | % | расход | кг | % |
| Сернокислый раствор, содержащий Fe, РЗЭ, Sc и др. | 1120000 | 99,83 | Сернокислый раствор | 1121921,73 | 100 |
| Железная стружка | 1921,73 | 0,17 | |||
| итого | 1121921,73 | 100 | итого | 1121921,73 | 100 |
0 комментариев