Навигация
Расчет пускового тока и момента
8. Расчет пускового тока и момента
При пуске в роторе АД имеют место два физических явления, оказывающих большое влияние на активное и индуктивное сопротивления, а следовательно, на пусковой ток и момент:
1) Эффект вытеснения тока в верхнюю часть паза, за счет которого расчетная высота паза и индуктивное сопротивление уменьшается, активное сопротивление увеличивается;
2) Эффект насыщения коронок зубцов потоками рассеяния, обусловленными большими пусковыми токами, за счет этого явления магнитные проводимости и индуктивные сопротивления уменьшаются.
Расчет активных и индуктивных сопротивлений обмотки ротора с учетом эффекта вытеснения тока.
Приведенная высота стержня для литой алюминиевой обмотки ротора при температуре 115˚С (класс изоляции F).
ξ = 63,61 · h21 = 63,61 · 0,040 = 2,54м
где h21 – высота стержня в пазу. Расчетный коэффициент увеличения активного сопротивления стержня φ в функции ξ. φ = 1,4. Глубина проникновения тока – расчетная высота стержня.
hr = h21 /(1 + φ) = 0,040/(1 + 1,4) = 0,017
Относительное увеличение активного сопротивления стержня.
kr = qc/qr = 96/81,33 = 1,18
где qr – площадь сечения стержня, ограниченная высотой hr.
qc – площадь сечения всего стержня.
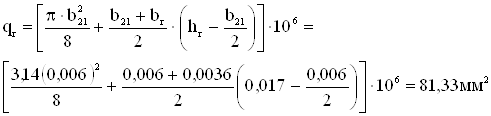
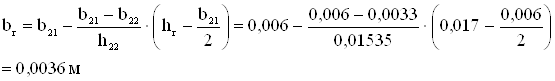
Коэффициент общего увеличения активного сопротивления фазы ротора за счет вытеснения тока.
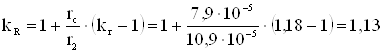
Приведенное активное сопротивление ротора с учетом вытеснения тока.
![]()
Расчетный коэффициент уменьшения индуктивного сопротивления стержня φ' в функции ξ. φ' = 0,6. Расчетный коэффициент уменьшения индуктивного сопротивления фазы ротора за счет вытеснения тока.
kx = λn2ξ /λ2 = 4,14/4,96 = 0,83
где λ2ξ – коэффициент магнитной проводимости рассеяния ротора с учетом вытеснения тока.
λ2ξ = λn2ξ + λл2 + λg2 = 1,23 + 2,1 + 0,81 = 4,14
λ2ξ = λn2 · φ' = 2,05 · 0,6 = 1,23
Приведенное индуктивное сопротивление ротора с учетом вытеснения тока.
x'2ξ =kx · x'2 = 0,83 · 0,17 = 0,14Ом
Расчет индуктивного сопротивления обмотки ротора с учетом влияния насыщения магнитопровода полями рассеяния.
Ток ротора, рассчитанный по Г-образной схеме замещения, без учета насыщения при S = 1.
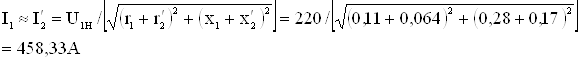
То же с учетом насыщения. I'2нас ≈ I1нас = I1 · kнас = 458,33 · 1,3 = 595,83А, где kнас – коэффициент насыщения, предварительно выбирается в пределах: kнас = 1,25 ÷ 1,4. Средняя МДС обмотки, отнесенная к одному пазу статора.
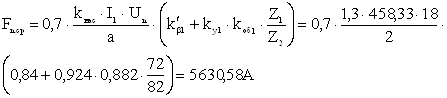
Фиктивная индукция потока рассеяния в воздушном зазоре.
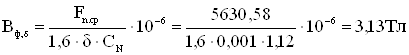
![]()
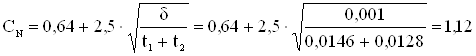
Коэффициент γδ, учитывающий отношение потока рассеяния при учете насыщения к потоку рассеяния ненасыщенной машины, по рис.8.
γδ = 0,8
Коэффициент магнитной индукции проводимости пазового рассеяния обмотки статора с учетом насыщения.
![]()

С1 = (t1-bш1) ·(1- γδ) = (0,0146 – 0,0045) · (1 – 0,80) = 0,00202
Коэффициент магнитной проводимости дифференциального рассеяния обмотки статора с учетом насыщения. λg1нас = λg1 · γδ = 1,13 · 0,8 = 0,9
Окончательное индуктивное сопротивление фазы обмотки статора с учетом насыщения, Ом
x1нас = x1 · ∑λ1нас/λ1 = 0,28 · 5,16/5,47 = 0,26 Ом
∑λ1нас = λn1нас + λg1нас + λл1 = 1,66 + 0,9 + 2,6 = 5,16
Аналогично для ротора: Коэффициент магнитной проводимости пазового рассеяния с учетом насыщения.
![]()
Δλn2нас = hш2/bш2 · С2/bш2 + С2 = 0,001/0,0015 · 0,00226/0,0015 + + 0,00226 = 0,4
С2 = (t2 – bш2) · (1- γδ) = (0,0128 – 0,0015) · (1- 0,80) = 0,00226
Коэффициент магнитной проводимости дифференциального рассеяния обмотки ротора с учетом насыщения.
λg2нас = λg2 · γδ = 0,81 · 0,8 = 0,65
Окончательно приведенное индуктивное сопротивление фазы обмотки ротора с учетом влияния вытеснения тока и насыщения.
x'2ξнас = x'2 · ∑λ2gнас/λ2 = 0,17 · 3,58/4,96 = 0,12Ом
∑λ2gнас = λn2нас + λg2нас + λл2 = 0,83 + 0,65 + 2,1 = 3,58
Коэффициент С1 в Г- образной схеме замещения.
С1nнас = 1 + (x1нас/x12n) = 1 + (0,26/14,92) = 1,02
x12n ≈ x12 · kμ = 13,2 · 1,13 = 14,92
Ток в обмотке ротора с учетом насыщения при S = 1.
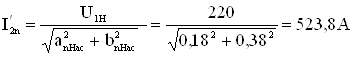
аnнас = r1 + C1nнас · r'2ξ = 0,11 + 1,02 · 0,072 = 0,18
bnнас =x1нас + C1nнас · x'2ξнас = 0,26 + 1,02 · 0,12 = 0,38
Ток в обмотке статора при S = 1.
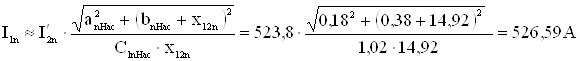
Пусковой ток в относительных единицах.
I1n* = I1n/I1н = 526,59/91,44 = 5,76
Кратность пускового момента.
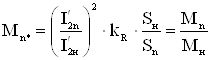 , Sn = 1
, Sn = 1
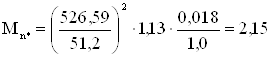
Mn = Mn* · Mн = 2,15 · 50 = 107,5H.м
СПИСОК ЛИТЕРАТУРЫ
1.Костенко Г.Н., Пиотровский Л.М. Электрические машины.- Л.: 1972.
2.Брускин Д.Э., Зорохович А.Е., Хвостов В.С.- Электрические машины. М.: 1979. Ч I. Ч II.
3.Кацман М.М. Электрические машины.- М.: 1983.
4.Копылов И.П. Электрические машины. -Л.: 1972.
5.Проектирование электрических машин. /Под ред. И.П.Копылова М.: 1980.
6.Зимин В.И., Каплай М.Я., Палей А.М. Обмотки электрических машин.- М.: 1975
7.Чичетян В.И. Электрические машины. Сборник задач.- М. : Высшая школа 1988.
Похожие работы
... дешевле сервоприводов. Шаговый привод как недорогая альтернатива сервоприводу наилучшим образом подходит для автоматизации отдельных узлов и систем, где не требуется высокая динамика. Заключение Электрические машины малой мощности имеют, как правило, закрытое конструктивное исполнение, рассчитанное на работу в любом положении в пространстве, длительные сроки сохраняемости. Конструкция этих ...
... с геометрической нейтрали в направлении вращения якоря у генераторов или встречно направлению вращения якоря у двигателей. Этот способ улучшения коммутации применим лишь в нереверсируемых электрических машинах, работающих с неизменной нагрузкой. Искрение на коллекторе является интенсивным источником электромагнитных колебаний частотой от 1000 до 3000 Гц. Эти колебания распространяются по сети и ...
... 4 Содержание отчета Схема включения однофазного счетчика в сеть. Схема включения трехфазного счетчика (п.7). Таблица с результатами измеренных и вычисленных значений. 3. Выводы о результатах поверки счетчика. Контрольные вопросы. 1. Единицы измерения электрической энергии. 2. Основные части счетчика и их назначение. 3. Принцип работы индукционного ...
... особенностью машины постоянного тока является наличие коллектора и скользящего контакта между обмоткой якоря и внешней электрической цепью. 2.2 Устройство машины постоянного тока Машина постоянного тока (рис. 2.3) по конструктивному исполнению подобна обращенной синхронной машине, у которой обмотка якоря расположена на роторе, а обмотка возбуждения – на статоре. Основное отличие заключается ...

0 комментариев