Навигация
Осевое усилие, передаваемое механизмом, которое прямопропорционально его нагрузочной способности
2. Осевое усилие, передаваемое механизмом, которое прямопропорционально его нагрузочной способности.
Введем следующие обозначения:
r – радиус вала;
R – для схемы US это радиус наружного кольца шарикоподшипника (ролика), а для схемы BRD – радиус отверстия внутреннего кольца шарикоподшипника;
r1 – радиус скругления внутреннего кольца шарикоподшипника (радиус оливажа);
![]() - угол поворота ролика или кольца.
- угол поворота ролика или кольца.
Для облегчения сравнения введем относительные величины:
![]() и
и ![]()
Сравнение ведем в следующих диапазонах:
![]()
![]()
![]()
![]()
Оценим габариты одной из основных частей механизма – однорядного шарикоподшипника. Рассчитаем размер вдоль вала валикокольцевого механизма (величину С), занимаемой половиной шарикоподшипника при повороте его на угол ![]() . Из рис. 2 следует, что
. Из рис. 2 следует, что
С = С1 + С2 (1)
![]() (2)
(2)
![]() (3)
(3)
где ![]()
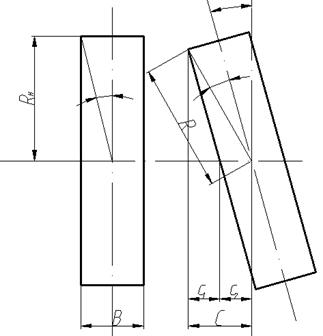
Рис. 2. К расчету габарита шарикоподшипника
После подстановки (2) и (3) в выражение (1) получим:
![]() ,
,
где ![]()
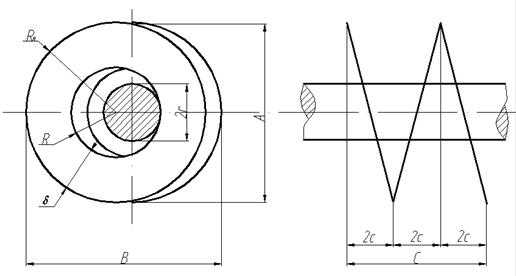 Рассчитаем теперь габариты валикокольцевого механизма по схеме вал-кольца:
Рассчитаем теперь габариты валикокольцевого механизма по схеме вал-кольца:
Рис. 3. К расчету габарита схемы вал-кольца (BRD)
Примем ![]() R (рис. 3), тогда получим
R (рис. 3), тогда получим
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Перемножая (6), (7) и (8) получим габарит занимаемый схемой вал-кольца:
![]() (8)
(8)
Рассчитаем габарит схемы вал-ролики:
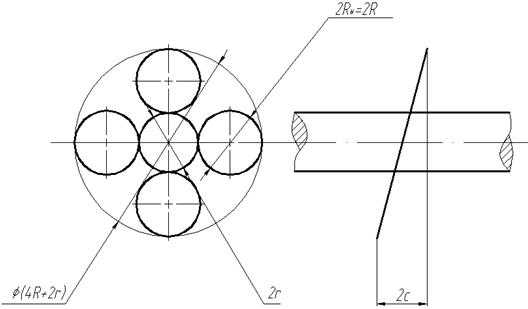
Рис. 4. К расчету габарита схемы вал-ролики (US)
![]() (9)
(9)
![]() (10)
(10)
Перемножив (9) и (10) получим габарит схемы вал-ролики:
![]() (11)
(11)
Производим сравнение габаритов схем (8) и (11). Принимая r = 1 и отбрасывая в каждой зависимости одинаковые сомножители, получаем:
![]() (12)
(12)
![]() (13)
(13)
Задаваясь значениями a, вычисляем габарит механизмов, результаты вычисления сводим в табл. 1 и строим графики на рис. 5.
Таблица 1.
Вычисление габаритов схем валикокольцевых механизмов (ВКМ)
| a |
|
|
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | - - - - - - 216,72 242,88 270,48 299,52 330 361,92 395,28 430,08 | 25,12 30,40 36,17 42,45 49,24 56,52 60,35 64,31 68,39 72,60 76,93 81,39 85,97 90,68 |
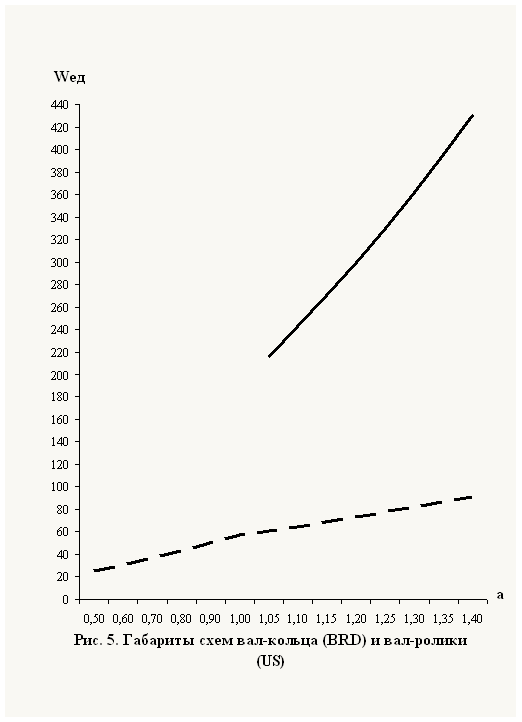
Из табл. 1 и рис. 5 видим, что габарит схемы вал-кольца значительно выше, чем схемы вал-ролики.
Сравнение по осевому усилию, передаваемому механизмом
Максимальная сила прижима ролика или кольца к валу определяется по формуле:
![]() кг (14) [
]
кг (14) [
]
где ![]() ,
, ![]()
Е1, Е2 – модуль упругости контактирующих тел.
Для стали Е = 2,12*106 кг/см2
![]() - допустимая величина контактного напряжения смятия
- допустимая величина контактного напряжения смятия
![]() - приведенный радиус кривизны
- приведенный радиус кривизны
![]() (15)
(15)
![]() - величины, обратные радиусам главных кривизн в плоскостях I и II вала в точке касания;
- величины, обратные радиусам главных кривизн в плоскостях I и II вала в точке касания;
![]() - величины, обратные радиусам главных кривизн в плоскостях I и II ролика (кольца) в точке касания;
- величины, обратные радиусам главных кривизн в плоскостях I и II ролика (кольца) в точке касания;
![]() и
и ![]() - коэффициенты, являющиеся функциями эмпирических интегралов, определяемые по величине
- коэффициенты, являющиеся функциями эмпирических интегралов, определяемые по величине ![]()
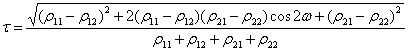 (16)
(16)
где ![]() - угол между соответствующими плоскостями главных сечений обоих соприкасающихся тел (
- угол между соответствующими плоскостями главных сечений обоих соприкасающихся тел (![]() ).
).
![]()
где ![]() - привиденный радиус кривизны при условии r = 1.
- привиденный радиус кривизны при условии r = 1.
[![]() ]П и
]П и ![]() зависят от выбора материала контактирующих тел и являются величинами cons1, поэтому сравнивать схемы вал-колца и вал-ролики на максимальное усилие прижима будем по величине
зависят от выбора материала контактирующих тел и являются величинами cons1, поэтому сравнивать схемы вал-колца и вал-ролики на максимальное усилие прижима будем по величине ![]() .
.
Рассчитаем приведенные радиусы кривизны для схем вал-кольца (BRD) по формуле (17):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
при r = 1
![]() (17)
(17)
Рассчитаем приведенные радиусы кривизны для схем вал-ролики (US) по формуле (18):
![]()
![]()
![]()
![]()
![]()
![]()
при r = 1
![]() (18)
(18)
Значения ![]() для схем ВКМ сведем в табл. 2.
для схем ВКМ сведем в табл. 2.
Таблица 2.
Единичные приведенные радиусы кривизны для схем BRD и US.
| а |
|
| |||||
| b = 0.5 | b = 1.0 | b = 1.5 | b = 2.0 | b = 2.5 | b = 3.0 | ||
| 0.50 0.60 0.70 0.80 0.90 1.00 1.05 1.10 1.15 1.20 1.25 1.30 1.35 1.40 | - - - - - - 0.488 0.478 0.469 0.462 0.455 0.448 0.443 0.438 | - - - - - - 0.955 0.917 0.885 0.857 0.833 0.813 0.794 0.778 | - - - - - - 1.400 1.320 1.255 1.200 1.154 1.114 1.080 1.050 | - - - - - - 1.826 1.692 1.586 1.500 1.429 1.368 1.317 1.273 | - - - - - - 2.234 2.037 1.885 1.765 1.667 1.585 1.517 1.458 | - - - - - - 2.625 2.357 2.156 2.000 1.875 1.773 1.688 1.615 | 0.333 0.375 0.412 0.444 0.474 0.500 0.512 0.524 0.535 0.546 0.556 0.565 0.574 0.583 |
Выведем ![]() по формуле (16) для относительных величи а и b для схем BRD и US.
по формуле (16) для относительных величи а и b для схем BRD и US.
Для схемы US:
![]()
![]()
![]()
![]()
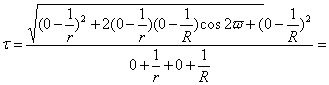
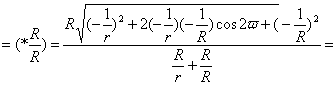
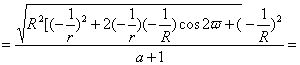
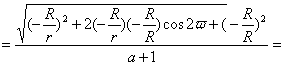
![]()
![]() (19)
(19)
Для схемы BRD:
![]()
![]()
![]()
![]()
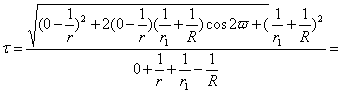
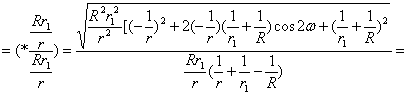
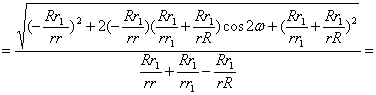
![]()
![]() (20)
(20)
Задаваясь значениями a, b и ![]() =В по формулам (19) и (20) вычислим значения
=В по формулам (19) и (20) вычислим значения ![]() для схем US и BRD, затем по значениям
для схем US и BRD, затем по значениям ![]() найдем коэффициенты
найдем коэффициенты ![]() и
и ![]() по таблицам 5, 6 и, наконец, найдем значения
по таблицам 5, 6 и, наконец, найдем значения ![]() для схем ВКМ.
для схем ВКМ.
а) Зададимся ![]() = В = 00.
= В = 00.
![]() при
при ![]() = В = 00:
= В = 00: ![]() = 1 и
= 1 и ![]() - неопределенность. Контакт линейный.
- неопределенность. Контакт линейный.
Для схем BRD формулу (20) упростим для данного случая ![]() = В = 00:
= В = 00:
![]()
![]()
![]()
![]() (21)
(21)
Знак «+» при ab > a+b
и «-» при ab < a+b
Значение ![]() рассчитываем для схемы BRD при
рассчитываем для схемы BRD при ![]() = В = 00 по формуле (21) и сводим в табл. 3.
= В = 00 по формуле (21) и сводим в табл. 3.
Таблица 3.
Значения ![]() при
при ![]() = В = 00
= В = 00
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 0,9535 0,9130 0,8776 0,8462 0,8182 0,7931 0,7705 0,7500 | 0,9091 0,8333 0,7692 0,7143 0,6667 0,6250 0,5882 0,5556 | 0,8667 0,7600 0,6727 0,6000 0,5385 0,4857 0,4400 0,4000 | 0,8261 0,6923 0,5862 0,5000 0,4286 0,3684 0,3171 0,2727 | 0,7872 0,6296 0,5082 0,4118 0,3333 0,2683 0,2135 0,1667 | 0,7500 0,5714 0,4375 0,3333 0,2500 0,1818 0,1250 0,0769 |
По значениям ![]() находим
находим ![]() по таблицам (5, 6) и сводим в табл. 4.
по таблицам (5, 6) и сводим в табл. 4.
Таблица 4.
Значения ![]() при
при ![]() = В = 00
= В = 00
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 1,655 1,465 1,370 1,311 1,269 1,239 1,215 1,197 | 1,452 1,291 1,214 1,169 1,137 1,115 1,095 1,084 | 1,347 1,206 1,141 1,102 1,079 1,062 1,050 1,039 | 1,281 1,153 1,094 1,067 1,047 1,033 1,024 1,018 | 1,233 1,117 1,069 1,042 1,027 1,017 1,010 1,006 | 1,197 1,089 1,049 1,027 1,014 1,007 1,004 1,002 |
Используя табл. 2 и 4 находим ![]() и сводим в табл. 5 и рис. 6
и сводим в табл. 5 и рис. 6
Таблица 5.
Значения ![]() при
при ![]() = В = 00
= В = 00
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 1,080 0,718 0,566 0,481 0,423 0,382 0,352 0,329 | 2,792 1,809 1,401 1,173 1,020 0,916 0,828 0,771 | 4,790 3,056 2,340 1,927 1,673 1,486 1,350 1,237 | 7,009 4,388 3,294 2,733 2,344 2,063 1,862 1,710 | 9,355 5,783 4,341 3,524 3,010 2,643 2,371 2,164 | 11,818 7,175 5,366 4,333 3,665 3,210 2,884 2,624 |
а) Зададимся ![]() = В = 50.
= В = 50.
По формулам (19) и (20) рассчитаем ![]() и
и ![]() при
при ![]() = В = 50. Значения сведем в табл. 6.
= В = 50. Значения сведем в табл. 6.
Таблица 6.
Значения ![]() и
и ![]() при
при ![]() = В = 50.
= В = 50.
| а |
|
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | ||
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | - - - - - - 0,9646 0,9240 0,8884 0,8569 0,8289 0,8037 0,7810 0,7605 | - - - - - - 0,9383 0,8621 0,7976 0,7424 0,6946 0,6528 0,6159 0,5832 | - - - - - - 0,9206 0,8130 0,7253 0,6524 0,5910 0,5386 0,4934 0,4542 | - - - - - - 0,9108 0,7758 0,6696 0,5841 0,5141 0,4560 0,4073 0,3663 | - - - - - - 0,9082 0,7493 0,6288 0,5350 0,4609 0,4016 0,3540 0,3159 | - - - - - - 0,9120 0,7323 0,6011 0,5029 0,4284 0,3719 0,3295 0,2683 | 0,9966 0,9964 0,9963 0,9962 0,9962 0,9962 0,9962 0,9962 0,9962 0,9962 0,9962 0,9963 0,9963 0,9963 |
По значениям ![]() и
и ![]() из табл. 6 найдем выражения
из табл. 6 найдем выражения ![]() и сведем в табл. 7
и сведем в табл. 7
Таблица 7.
Значения ![]() и
и ![]() при
при ![]() = В = 50.
= В = 50.
| а |
|
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | ||
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | - - - - - - 1,746 1,504 1,395 1,329 1,285 1,251 1,226 1,207 | - - - - - - 1,567 1,338 1,244 1,190 1,155 1,128 1,110 1,093 | - - - - - - 1,492 1,263 1,177 1,128 1,097 1,079 1,065 1,053 | - - - - - - 1,463 1,221 1,139 1,093 1,071 1,054 1,041 1,033 | - - - - - - 1,450 1,196 1,117 1,078 1,055 1,040 1,031 1,024 | - - - - - - 1,461 1,181 1,102 1,068 1,047 1,034 1,027 1,022 | 2,736 2,706 2,692 2,678 2,678 2,678 2,678 2,678 2,678 2,678 2,678 2,692 2,692 2,692 |
Используя табл. 2 и табл. 7 находим ![]() и
и ![]() и сводим в табл. 8 и рис. 7.
и сводим в табл. 8 и рис. 7.
Таблица 8.
Значения ![]() при
при ![]() = В = 50.
= В = 50.
Какая-то фигня, таблица перечеркнута (на стр. 48)
в) Зададимся ![]() = В = 100.
= В = 100.
По формулам (19) и (20) рассчитаем ![]() и
и ![]() при
при ![]() = В = 100. Значения сведем в табл. 9.
= В = 100. Значения сведем в табл. 9.
Таблица 9.
Значения ![]() и
и ![]() при
при ![]() = В = 100.
= В = 100.
| а |
|
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | ||
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | - - - - - - 0,9970 0,9560 0,9200 0,8881 0,8597 0,8343 0,8114 0,7907 | - - - - - - - 0,9423 0,8765 0,8202 0,7715 0,7290 0,6917 0,6586 | - - - - - - - 0,9533 0,8627 0,7877 0,7249 0,6715 0,6258 0,5862 | - - - - - - - 0,9829 0,8714 0,7822 0,7097 0,6499 0,6001 0,5582 | - - - - - - - - 0,8958 0,7955 0,7164 0,6530 0,6018 0,5600 | - - - - - - - - 0,9360 0,8210 0,7369 0,6715 0,6201 0,5793 | 0,9865 0,9858 0,9853 0,9850 0,9849 0,9848 0,9848 0,9848 0,9849 0,9849 0,9850 0,9851 0,9851 0,9852 |
По значениям ![]() и
и ![]() из табл. 9 найдем выражения
из табл. 9 найдем выражения ![]() и сведем в табл. 10.
и сведем в табл. 10.
Таблица 10.
Значения ![]() и
и ![]() при
при ![]() = В = 100.
= В = 100.
| а |
|
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | ||
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | - - - - - - 2,800 1,672 1,490 1,394 1,334 1,292 1,261 1,237 | - - - - - - - 1,586 1,368 1,272 1,217 1,179 1,153 1,132 | - - - - - - - 1,654 1,339 1,233 1,176 1,140 1,115 1,094 | - - - - - - - 2,010 1,357 1,228 1,166 1,127 1,102 1,085 | - - - - - - - - 1,416 1,241 1,171 1,129 1,103 1,086 | - - - - - - - - 1,532 1,274 1,185 1,140 1,112 1,091 | 2,131 2,086 2,066 2,060 2,056 2,052 2,052 2,052 2,056 2,056 2,060 2,062 2,062 2,064 |
Пользуясь табл. 2 и табл. 10 находим ![]() и сводим в табл. 11 и рис. 8.
и сводим в табл. 11 и рис. 8.
Таблица 11.
Значения ![]() при
при ![]() = В = 100.
= В = 100.
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 5,228 1,068 0,728 0,578 0,491 0,433 0,394 0,363 | - 3,355 2,005 1,512 1,251 1,083 0,966 0,878 | - 7,884 3,781 2,699 2,166 1,839 1,617 1,444 | - 23,248 6,286 4,167 3,237 2,679 2,321 2,070 | - - 10,088 5,954 4,462 3,615 3,088 2,723 | - - 16,714 8,271 5,850 4,657 3,918 3,387 |
г) Зададимся ![]() = В = 150.
= В = 150.
По формуле (19) рассчитаем ![]() при
при ![]() = В = 150, затем по значениям
= В = 150, затем по значениям ![]() найдем
найдем ![]() и , наконец,
и , наконец, ![]() .
.
Все эти данные сведем в табл. 12 и отобразим график ![]() при
при ![]() = В = 150 на рис. 6.
= В = 150 на рис. 6.
Таблица 12.
Значения ![]() ,
, ![]() и
и ![]() при
при ![]() = В = 150
= В = 150
| а |
|
|
|
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 0,9698 0,9681 0,9670 0,9664 0,9660 0,9659 0,9659 0,9660 0,9661 0,9662 0,9664 0,9665 0,9667 0,9669 | 1,801 1,785 1,770 1,765 1,761 1,760 1,760 1,761 1,762 1,763 1,765 1,766 1,767 1,769 | 0,648 0,800 0,941 1,084 1,227 1,363 1,429 1,499 1,566 1,634 1,700 1,758 1,818 1,882 |
ВСТАВИТ РИС. (стр. 54-55)
Усилие подачи PS зависит от силы прижима Р. При исполнении привода с тремя кольцами, средние кольца прижимается с силой Р, крайние – с силой Р/2 (лист 1, рис. 8), поэтому (формула 1)
![]() ,
,
где ![]() - коэффициент трения.
- коэффициент трения.
В схеме US усилие подачи может быть увеличено за счет увеличения количества роликов. Поэтому
![]() (22)
(22)
где к – количество роликов,
![]() - коэффициент трения.
- коэффициент трения.
Подставляя в формулу (1) и формулу (22) значение Р из формулы (14) и отбросив одинаковые сомножители из обоих получившихся выражений, получим при r = 1:
![]() (23)
(23)
![]() (24)
(24)
Используя табл. 5, табл. 8, табл. 11 и табл. 12 составим таблицы значений выражений ![]() и
и ![]() для различных углов
для различных углов ![]() = В и строим графики на рис. 11, 12, 13.
= В и строим графики на рис. 11, 12, 13.
Таблица 13.
Значения ![]() при
при ![]() = В = 00
= В = 00
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 2,160 1,436 1,132 0,962 0,846 0,764 0,704 0,658 | 5,584 3,618 2,802 2,346 2,040 1,832 1,656 1,542 | 9,580 6,112 4,680 3,854 3,346 2,972 2,700 2,474 | 14,018 8,776 6,588 5,466 4,688 4,126 3,724 3,420 | 18,710 11,566 8,682 7,048 6,020 5,286 4,742 4,328 | 23,636 14,350 10,732 8,666 7,330 6,420 5,768 5,248 |
Таблица 14.
Значения ![]() при
при ![]() = В = 50
= В = 50
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 2,536 1,554 1,194 1,002 0,878 0,786 0,724 0,674 | 7,018 4,028 3,016 2,476 2,138 1,898 1,724 1,580 | 13,020 7,020 4,894 4,134 3,516 3,118 2,818 2,574 | 20,882 10,422 7,434 5,576 5,018 4,382 3,914 3,572 | 30,430 14,198 9,904 7,806 6,526 5,652 5,044 4,566 | 42,978 18,302 12,442 9,746 8,070 6,950 6,172 5,568 |
Таблица 15.
Значения ![]() при
при ![]() = В = 100
= В = 100
| а |
| |||||
| b = 0,5 | b = 1,0 | b = 1,5 | b = 2,0 | b = 2,5 | b = 3,0 | |
| 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 10,456 2,136 1,456 1,156 0,982 0,866 0,778 0,726 | - 6,710 4,010 3,024 2,502 2,166 1,932 1,756 | - 15,768 7,562 5,398 4,332 3,678 3,234 2,888 | - 46,496 12,572 8,334 6,474 5,358 4,642 4,140 | - - 20,176 11,908 8,924 7,230 6,176 5,446 | - - 33,428 16,542 11,700 9,314 7,836 6,774 |
Таблица 16.
Значения ![]() при
при ![]() = В = 50
= В = 50
| а |
| |||||
| k = 1 | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 | |
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 2,271 2,786 3,311 3,786 4,315 4,801 5,035 5,273 5,497 5,726 5,937 6,228 6,428 6,631 | 4,542 5,572 6,622 7,572 8,630 9,602 10,070 10,546 10,994 11,452 11,874 12,456 12,856 13,262 | 6,813 8,358 9,933 11,358 12,945 14,403 15,105 15,819 16,491 17,178 17,811 18,684 19,284 19,893 | 9,084 11,144 13,244 15,144 17,260 19,204 20,140 21,092 21,988 22,904 23,748 24,912 25,712 26,524 | 11,355 13,930 16,555 18,930 21,575 24,005 25,175 26,365 27,485 28,630 29,685 31,140 32,140 33,155 | 13,626 16,716 19,866 22,716 25,890 28,806 30,210 31,638 32,982 34,356 35,622 37,368 38,568 39,786 |
Таблица 17.
Значения ![]() при
при ![]() = В = 100
= В = 100
| а |
| |||||
| k = 1 | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 | |
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 1,073 1,276 1,497 1,723 1,953 2,160 2,265 2,372 2,488 2,591 2,702 2,799 2,889 2,989 | 2,146 2,552 2,994 3,446 3,906 4,320 4,530 4,744 4,976 5,182 5,404 5,598 5,778 5,978 | 3,219 3,828 4,491 5,169 5,859 6,480 6,795 7,116 7,464 7,773 8,106 8,397 8,667 8,967 | 4,292 5,104 5,988 6,892 7,812 8,640 9,060 9,488 9,952 10,364 10,808 11,196 11,556 11,956 | 5,365 6,380 7,485 8,615 9,765 10,800 11,325 11,860 12,440 12,955 13,510 13,995 14,445 14,945 | 6,438 7,656 8,982 10,338 11,718 12,960 13,590 14,232 14,928 15,546 16,212 16,794 17,334 17,934 |
Таблица 18.
Значения ![]() при
при ![]() = В = 150
= В = 150
| а |
| |||||
| k = 1 | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 | |
| 0,50 0,60 0,70 0,80 0,90 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 | 0,648 0,800 0,941 1,084 1,227 1,363 1,429 1,499 1,566 1,634 1,700 1,758 1,818 1,882 | 1,296 1,600 1,882 2,168 2,454 2,726 2,858 2,998 3,132 3,268 3,400 3,516 3,636 3,764 | 1,944 2,400 2,823 3,252 3,681 4,089 4,287 4,497 4,698 4,902 5,100 5,274 5,454 5,646 | 2,592 3,200 3,764 4,336 4,908 5,452 5,716 5,996 6,264 6,536 6,800 7,032 7,272 7,528 | 3,240 4,000 4,705 5,420 6,135 6,815 7,145 7,495 7,830 8,170 8,500 8,790 9,090 9,410 | 3,888 4,800 5,646 6,504 7,362 8,178 8,574 8,994 9,396 9,804 10,200 10,548 10,908 11,292 |
Осевая нагрузка, передаваемая схемой US, как видно из вышеприведенного, может быть увеличена за счет увеличения количества роликов и за счет увеличения относительной величины a = R/r.
Рассмотрим, выигрышно ли с точки зрения увеличения передаваемой осевой силы увеличение количества роликов за счет уменьшения a = R/r.
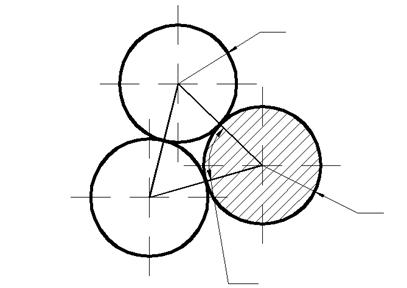 Определим максимальное значение a = R/r при заданном количестве роликов.
Определим максимальное значение a = R/r при заданном количестве роликов.
Рис. 9. Максимальное заполнение габарита ВКМ роликами.
АО = R + r
Из треугольника ![]() ОСА имеем
ОСА имеем ![]()
![]()
Домножим числитель и знаменатель на один и тот же член 1/2r, получим:
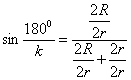 , т.к.
, т.к. ![]() , то
, то ![]()
Домножим числитель и знаменатель правой части на один и тот же множитель а.
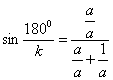
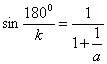
![]()
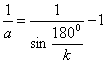
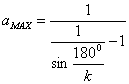 (25)
(25)
По значению ![]() из формулы (25) найдем по формуле (19)
из формулы (25) найдем по формуле (19) ![]() , затем
, затем ![]() ,
, ![]() и наконец
и наконец ![]() , найдем также
, найдем также ![]() по формуле (13) и все данные сведем в табл. 19 и рис. 10.
по формуле (13) и все данные сведем в табл. 19 и рис. 10.
Таблица 19.
| k |
|
|
|
|
при |
при |
|
| 2 3 4 5 6 7 8 |
6,46 2,41 1,43 1,00 0,785 0,611 | - 0,866 0,707 0,588 0,500 0,434 0,383 | - 0,9843 0,9718 0,9670 0,9659 0,9664 0,9679 | - 2,036 1,826 1,774 1,764 1,769 1,783 | - 6,329 3,043 1,917 1,363 | - 18,988 12,173 9,586 8,178 | - 1216,85 212,72 93,57 56,52 |
Добавить рис. На стр.64-66
Из табл. 19 и рис. 10 видим, что для схемы US увеличение количества роликов за счет уменьшения их диаметров (т.е. уменьшения a = R/r) уменьшает осевую силу, развиваемую механизмом, но в то же время значительно уменьшает и габариты механизма. Также замечаем, что для k = 6 ![]() =1,00, значит для однорядного расположения роликов при k = 6 a = R/r должно быть меньше 1.
=1,00, значит для однорядного расположения роликов при k = 6 a = R/r должно быть меньше 1.
Рассмотрим работу валикокольцевых механизмов раскладки при максимальном рассматриваемом нами угле поворота В = 150. Максимальное усилие прижима должно быть рассчитано при минимальной нагрузочной способности механизма, т.к. во время работы угол В изменяе6тся при реверсе механизма от максимального В = 150 до минимального В = 00 и снова до максимального В = 150, но уже в противоположную сторону.
Минимальная нагрузочная способность ВКМ по схеме вал-ролики (US) при угле В = 150, а по схеме вал-кольца (BRD) при угле В = 00, поэтому усилие прижима роликов или колец к валу должно рассчитываться при этих углах. А значит и сравнение механизмов по передаваемой осевой силе нужно проводить при этих углах, т.е. при ![]() = В = 150 для схемы US. Сравнение по осувой силе, передаваемой ВКМ ведем по выражениям
= В = 150 для схемы US. Сравнение по осувой силе, передаваемой ВКМ ведем по выражениям ![]()
![]() .
.
Выводы
1. При увеличении относительной величины a = R/r нагрузочная способность, а значит и осевое усилие, которое может передать механизм, у схемы вал-ролики (US) возрастает, а у схемы вал-кольца (BRD) убывает.
2. Относительная величина ![]() оказывает значительное влияние на нагрузочную способность схемы вал-кольца (BRD). При увеличении
оказывает значительное влияние на нагрузочную способность схемы вал-кольца (BRD). При увеличении ![]() осевое усилие, которое может передать механизм, возрастает и возрастает тем сильнее, чем меньеш a = R/r.
осевое усилие, которое может передать механизм, возрастает и возрастает тем сильнее, чем меньеш a = R/r.
3. С увеличением угла разворота В нагрузочная способность схемы вал-ролики (US) убывает, а схемы вал-кольца (BRD) возрастает. Минимальная нагрузочная способность схемы US при В = 150, схемы BRD при В = 00.
4. Сравнение схем по нагрузочной способности нужно вести при минимальной нагрузочной способности, т.е. при В = 150 для схемы US и В = 00 для схемы BRD.
5. Увеличение количества роликов для схемы US увеличивает нагрузочную способность и при большом количестве роликов k схема US может конкурировать по нагрузочной способности со схемой BRD. Но увеличение количества роликов значительно усложняет конструкцию механизма и может привести к появлению нежелательных напряжений в опорах вала, поэтому применение большого количества роликов нецелесообразно.
0 комментариев