Навигация
Исследование апериодического звена 1-го порядка
2. Исследование апериодического звена 1-го порядка
a. Исследование частотных характеристик апериодического звена 1-го порядка
Для исследования частотных характеристик апериодического звена 1-го порядка в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 11, для трех значений ![]() :
:
![]() .
.
Логарифмические частотные характеристики апериодических звеньев представлены на рисунке 12, графики переходной функции – на рисунке 13.
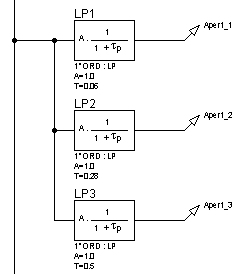
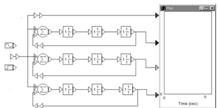
Рисунок 11 – Структурная схема для исследования апериодических звеньев 1-го порядка
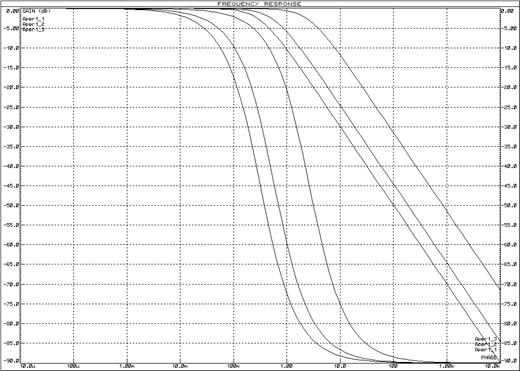
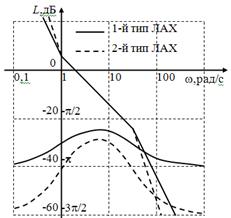
Рисунок 12 – Логарифмические частотные характеристики апериодических звеньев 1-го порядка
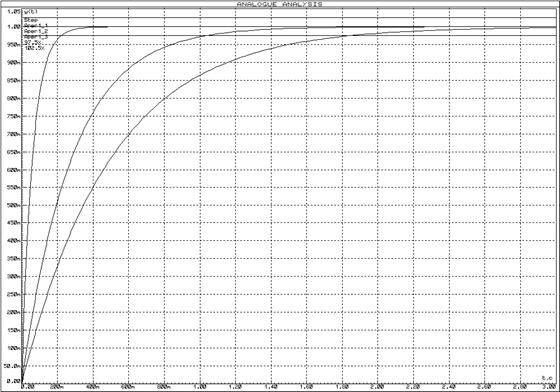
Рисунок 13 – Переходные функции апериодических звеньев 1-го порядка
b. Реализация апериодического звена 1-го порядка
Реализуем апериодическое звено 1-го порядка с постоянной времени ![]() на
на ![]() -цепочке и на
-цепочке и на ![]() -цепочке (рисунок 14). ЛАЧХ и ЛФЧХ
-цепочке (рисунок 14). ЛАЧХ и ЛФЧХ ![]() -цепочки и на
-цепочки и на![]() -цепочки представлены на рисунке 15, а и 15, б. Для сравнения частотных характеристик идеальных и реальных апериодических звеньев изобразим их ЛЧХ в совмещенных координатах (рисунок 15, в).
-цепочки представлены на рисунке 15, а и 15, б. Для сравнения частотных характеристик идеальных и реальных апериодических звеньев изобразим их ЛЧХ в совмещенных координатах (рисунок 15, в).

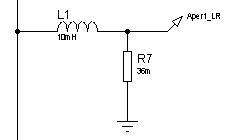
а)б)
а) ![]() -цепочка;
-цепочка;
б) ![]() -цепочка
-цепочка
Рисунок 14 – Электрическая принципиальная схема апериодических звеньев 1-го порядка с постоянной времени ![]()
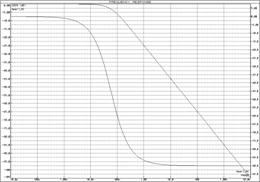

а) б)
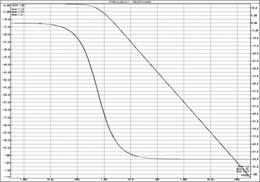
в)
Рисунок 15 – ЛАЧХ и ЛФЧХ апериодических звеньев
а) ![]() -цепочка; б)
-цепочка; б) ![]() -цепочка; в) совмещенные ЛЧХ идеального апериодического звена,
-цепочка; в) совмещенные ЛЧХ идеального апериодического звена, ![]() -цепочка и
-цепочка и ![]() -цепочка
-цепочка
При анализе частотных характеристик апериодических звеньев 1-го порядка можно сделать следующие выводы:
· увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).
· чем меньше постоянная времени Т, тем шире полоса пропускания (т.к.![]() ~
~![]() ).
).
· при уменьшении постоянной времени уменьшается время переходного процесса и наоборот.
· чем меньше постоянная времени, тем меньше время переходного процесса и шире полоса пропускания, следовательно, чем меньше время переходного процесса, тем шире полоса пропускания.
· если на график ЛАЧХ заменить ломаной кривой и из точки ''разлома'' опустить прямую на ось ![]() , то это и будет сопрягающая частота. Постоянную времени можно определить, зная сопрягающую частоту
, то это и будет сопрягающая частота. Постоянную времени можно определить, зная сопрягающую частоту ![]() :
: ![]() .
.
c. Исследование частотных характеристик апериодического звена 2-го порядка
Для исследования частотных характеристик апериодического звена 2-го порядка в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 16, при неизменной первой постоянной времени ![]() и для трех значений
и для трех значений ![]() :
:
![]() .
.
Логарифмические частотные характеристики апериодических звеньев 2-го порядка представлены на рисунке 17, графики переходной функции – на рисунке 18.
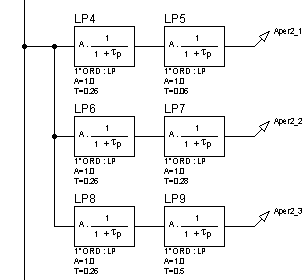
Рисунок 16 – Структурная схема для исследования апериодических звеньев 2-го порядка

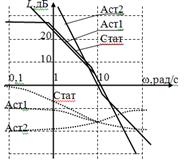
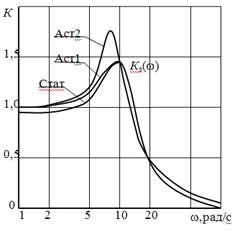
Рисунок 17 – Логарифмические частотные характеристики апериодических звеньев 2-го порядка
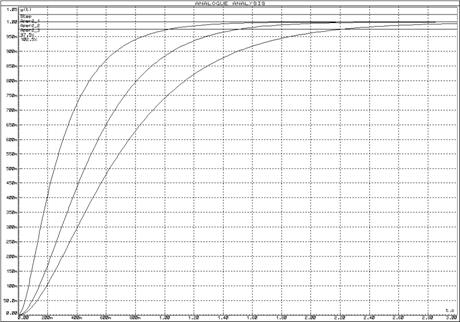
Рисунок 18 – Переходные функции апериодических звеньев 2-го порядка
d. Реализация апериодического звена 2-го порядка
Попробуем реализовать апериодическое звено 2-го порядка с постоянными времени ![]() и
и ![]() на двух последовательно соединенных
на двух последовательно соединенных ![]() -цепочках, отдельно каждая из которых представляет собой апериодическое звено 1-го порядка (рисунок 19). ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го порядка представлены на рисунке 20, а, а их переходные функции – на рисунке 20, б.
-цепочках, отдельно каждая из которых представляет собой апериодическое звено 1-го порядка (рисунок 19). ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го порядка представлены на рисунке 20, а, а их переходные функции – на рисунке 20, б.
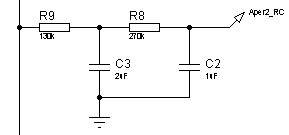
Рисунок 19 – Электрическая принципиальная схема двух последовательно соединенных апериодических звеньев 1-го порядка с постоянными времени ![]() и
и ![]()
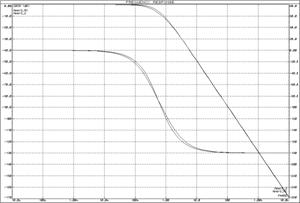

а)б)
а) ЛАЧХ и ЛФЧХ; б) переходная функция
Рисунок 20 – Характеристики последовательно соединенных ![]() -цепочек
-цепочек
Реализуем апериодическое звено 2-го порядка с постоянными времени ![]() и
и ![]() на двух последовательно соединенных
на двух последовательно соединенных ![]() -цепочках, разделенных промежуточным (разделяющим, развязывающим) усилителем (повторителем) (рисунок 21). ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го порядка представлены на рисунке 22, а, а их переходные функции – на рисунке 22, б.
-цепочках, разделенных промежуточным (разделяющим, развязывающим) усилителем (повторителем) (рисунок 21). ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го порядка представлены на рисунке 22, а, а их переходные функции – на рисунке 22, б.

Рисунок 21 – Электрическая принципиальная схема двух ![]() -цепочек с постоянными времени
-цепочек с постоянными времени ![]() и
и ![]() , разделенных операционным усилителем
, разделенных операционным усилителем
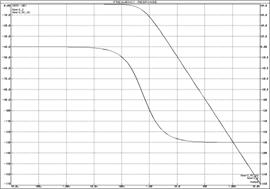

а) б)
а) ЛАЧХ и ЛФЧХ;
б) переходная функция
Рисунок 22 – Характеристики последовательно соединенных ![]() -цепочек с разделительным усилителем
-цепочек с разделительным усилителем
При анализе частотных характеристик апериодических звеньев 2-го порядка можно сделать следующие выводы:
· увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).
· увеличение (уменьшение) постоянной времени звена приводит к увеличению (уменьшению) времени переходного процесса.
· на полосу пропускания большее влияние оказывает большая постоянная времени
· при увеличении постоянной времени звена время переходного процесса увеличивается, а полоса пропускания уменьшается, следовательно, при увеличении времени переходного процесса полоса пропускания уменьшается и наоборот.
e. Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка
Ввиду того, что апериодическое звено 2-го порядка можно аппроксимировать звеном 1-го порядка, если одна постоянная времени намного превышает вторую (![]() в 10 раз), сравним характеристики звена с постоянными времени
в 10 раз), сравним характеристики звена с постоянными времени ![]() и
и ![]() со звеном 1-го порядка, изображенным на рисунке 23.
со звеном 1-го порядка, изображенным на рисунке 23.
Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка

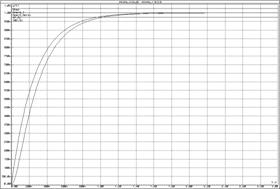
а) б)
а) ЛАЧХ и ЛФЧХ;б) переходные функции
Рисунок 24 – Характеристики апериодического звена 2-го порядка и инерционного звена
При анализе характеристик апериодических звеньев (рисунок 24) можно сделать следующие выводы:
· апериодическое звено 2-го порядка можно аппроксимировать апериодическим звеном 1-го порядка, если первая постоянная времени намного меньше второй, т.к. в таком случае влияние первой экспоненты на форму выходного сигнала несущественно.
Исследование колебательного звена
При исследовании колебательного звена необходимо пронаблюдать за характером его частотных характеристик при изменении постоянной времени и декремента затухания в пределах, указанных в индивидуальном задании. Т.е. необходимо исследовать частотные характеристики при постоянных времени ![]() и декременте затухания
и декременте затухания ![]() .
.
f. Исследование частотных характеристик колебательного звена при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)
Для исследования колебательного звена при изменении постоянной времени (![]() ) и неизменном декременте затухания в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 25. Логарифмические частотные характеристики колебательного звена представлены на рисунке 26, графики переходной функции – на рисунке 27.
) и неизменном декременте затухания в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 25. Логарифмические частотные характеристики колебательного звена представлены на рисунке 26, графики переходной функции – на рисунке 27.

Рисунок 25 – Структурная схема для исследования колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)

Рисунок 26 – Логарифмические частотные характеристики колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)

Рисунок 27 – Переходные функции колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)
g. Исследование частотных характеристик колебательного звена при изменении постоянной времени (![]() ) и неизменном коэффициенте демпфирования (
) и неизменном коэффициенте демпфирования (![]() )
)
Для исследования колебательного звена при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() ) в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 28. Логарифмические частотные характеристики колебательного звена представлены на рисунке 29, графики переходной функции – на рисунке 30.
) в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 28. Логарифмические частотные характеристики колебательного звена представлены на рисунке 29, графики переходной функции – на рисунке 30.
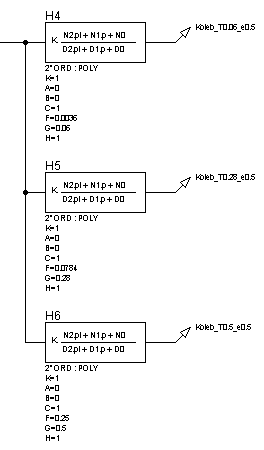
Рисунок 28 – Структурная схема для исследования колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)
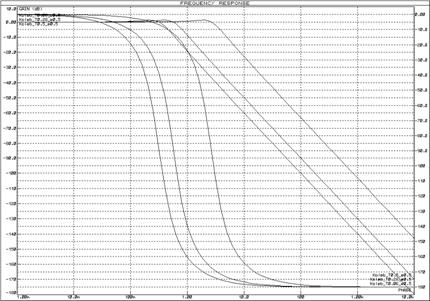
Рисунок 29 – Логарифмические частотные характеристики колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)

Рисунок 30 – Переходные функции колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)
h. Исследование частотных характеристик колебательного звена при неизмененной постоянной времени (![]() ) и изменении декремента затухания (
) и изменении декремента затухания (![]() ).
).
Для исследования колебательного звена при неизмененной постоянной времени (![]() ) и изменении коэффициента демпфирования (
) и изменении коэффициента демпфирования (![]() ) в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 31. Логарифмические частотные характеристики колебательного звена представлены на рисунке 32, графики переходной функции – на рисунке 33.
) в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 31. Логарифмические частотные характеристики колебательного звена представлены на рисунке 32, графики переходной функции – на рисунке 33.
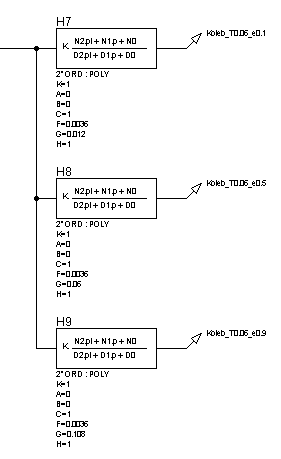
Рисунок 31 – Структурная схема для исследования колебательного звена при неизмененной постоянной времени (![]() ) и изменении декремента затухания (
) и изменении декремента затухания (![]() )
)

Рисунок 32 – Логарифмические частотные характеристики колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте затухания (
) и неизменном декременте затухания (![]() )
)
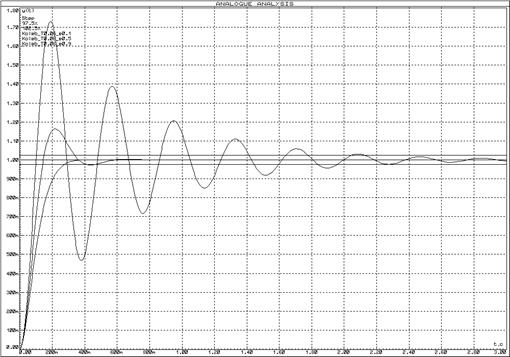
Рисунок 33 – Переходные функции колебательного звена при неизмененной постоянной времени (![]() ) и изменении декремента затухания (
) и изменении декремента затухания (![]() )
)
i. Реализация колебательного звена
Реализуем колебательное звено с постоянной времени ![]() и коэффициентом демпфирования
и коэффициентом демпфирования ![]() на
на ![]() -контуре (рисунок 34). ЛАЧХ и ЛФЧХ данного звена и необходимого колебательного звена представлены на рисунке 35, а, а их переходные функции – на рисунке 35, б.
-контуре (рисунок 34). ЛАЧХ и ЛФЧХ данного звена и необходимого колебательного звена представлены на рисунке 35, а, а их переходные функции – на рисунке 35, б.
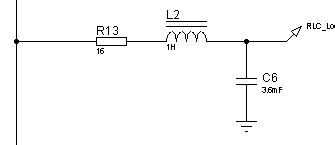
Рисунок 34 – Электрическая принципиальная схема колебательного ![]() -контура
-контура
а) б)
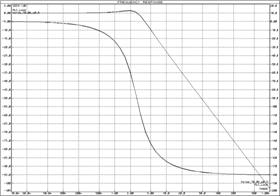
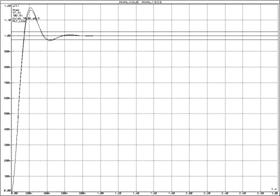
а) ЛАЧХ и ЛФЧХ;б) переходная функция
Рисунок 35 – Характеристики колебательного звена и ![]() -контура
-контура
При анализе графиков частотных характеристик и переходных процессов (рисунок 35) колебательных звеньев можно сделать следующие выводы:
· увеличение (уменьшение) постоянной времени звена при неизменном декременте затухания приводит к сдвигу частотных характеристик влево (вправо).
· при неизменном коэффициенте демпфирования увеличение постоянной времени звена приводит к сужению полосы пропускания; колебательность переходного процесса не меняется.
· при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) колебательности переходного процесса и к более плавной ЛФЧХ.
· при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) перерегулирования, сужению (расширению) полосы пропускания и уменьшению (увеличению) колебательности.
Похожие работы
... природе, а по их динамическим свойствам. Для построения систем управления необходимо знание характеристик типовых звеньев. Основными характеристиками звеньев являются дифференциальное уравнение и передаточная функция. Рассмотрим основные звенья и их характеристики. Усилительное звено (безынерционное, пропорциональное). Усилительным называют звено, которое описывается уравнением: (2) или ...
... работы Целью работы является анализ частотных характеристик разомкнутых и замкнутых систем, получение навыков по использованию критерия устойчивости Найквиста. В работе предусматривается исследование трех систем, различающихся видом передаточной функции (ПФ) разомкнутого контура. Варианты значений параметров ПФ приведены в табл. 3.1. Замкнутая система построена по типу классической следящей ...
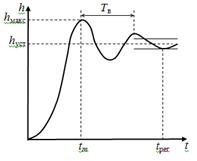
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
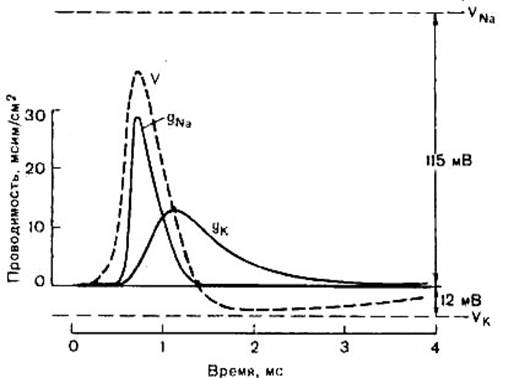
... к совокупностям с одинаковыми параметрами проверяли с помощью рангового U - критерия Манна-Уитни. Глава 3. Результаты и обсуждение Был проведено исследование функциональных характеристик нервно-мышечного аппарата верхних конечностей, в частности кисти правой руки. Для анализа был выбран стимуляционный электромиографический метод. Для выявления особенностей биоэлектрического ответа скелетных ...


0 комментариев