Исследование дифференцирующих звеньев

3.   Исследование дифференцирующих звеньев

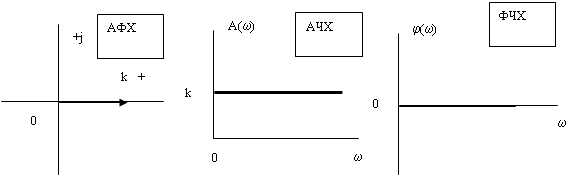
a.   Исследование частотных характеристик идеального дифференцирующего звена

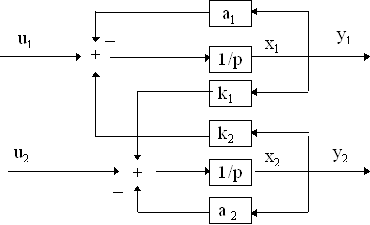
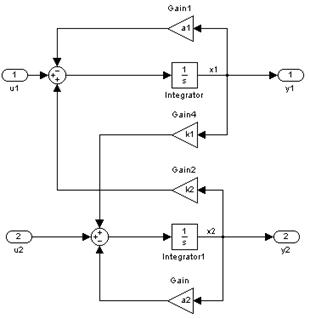
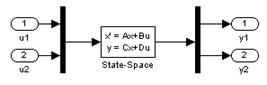
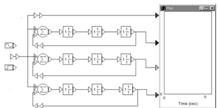
Для исследования частотных характеристик идеального дифференцирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 36. Логарифмические частотные характеристики идеального дифференцирующего звена представлены на рисунке 37, график переходной функции – на рисунке 38.

Рисунок 36 – Структурная схема для исследования идеального дифференцирующего звена

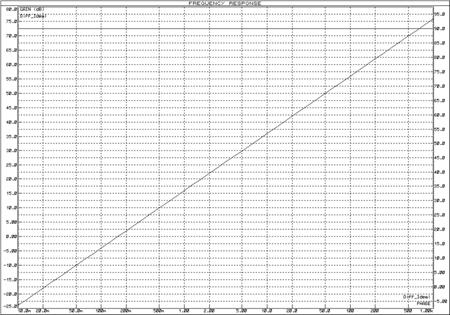
Рисунок 37 – Логарифмические частотные характеристики идеального дифференцирующего звена

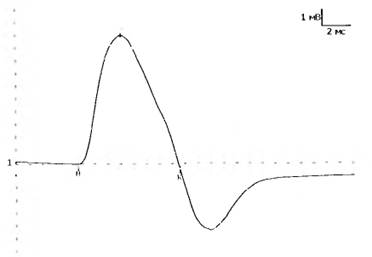
Рисунок 38 – Переходная функция идеального дифференцирующего звена

b.   Реализация идеального дифференцирующего звена

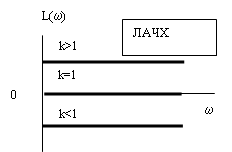
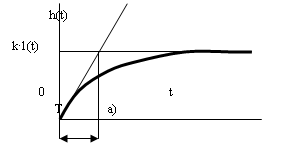
Реализуем идеальное дифференцирующее звено схемой, изображенной на рисунке 39. ЛАЧХ и ЛФЧХ дифференцирующего звена представлены на рисунках 40 и 41, переходная функция – на рисунке 42.

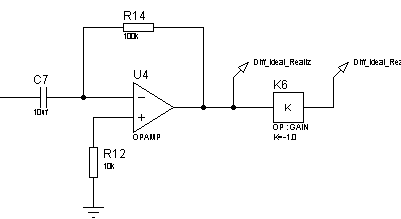
Рисунок 39 – Электрическая принципиальная схема дифференцирующего звена

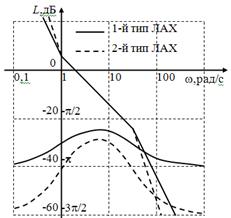
Рисунок 40 – ЛАЧХ и ЛФЧХ дифференцирующего звена

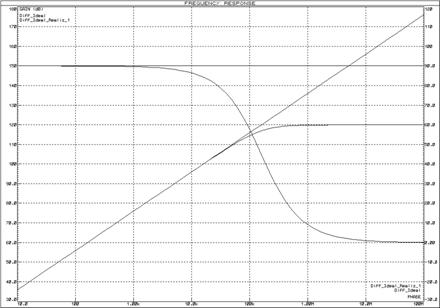
Рисунок 41 – ЛАЧХ и ЛФЧХ дифференцирующего звена с инвертором

а)

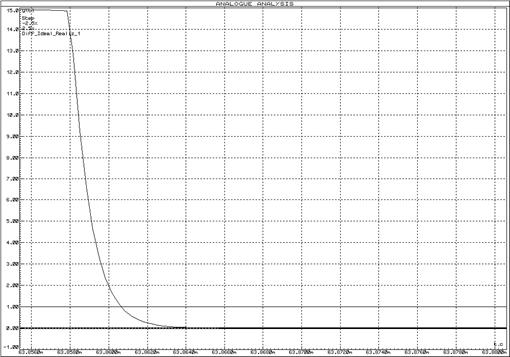
б)

Рисунок 42 – Переходная функция схемы реализации идеального дифференцирующего звена

c.    Исследование частотных характеристик реального дифференцирующего звена

Для исследования частотных характеристик реального дифференцирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 43. Логарифмические частотные характеристики реального дифференцирующего звена представлены на рисунке 44, переходные функции – на рисунке 45.

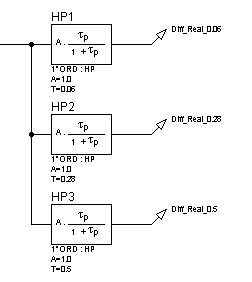
Рисунок 43 – Структурная схема для исследования реального дифференцирующего звена

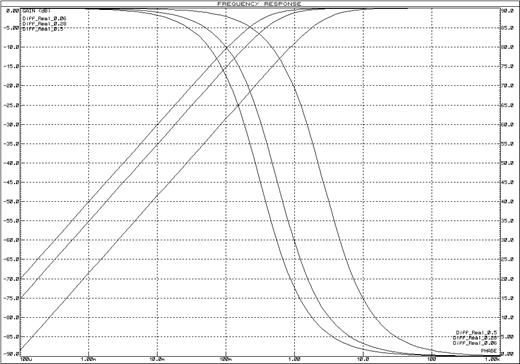
Рисунок 44 – Логарифмические частотные характеристики реального дифференцирующего звена

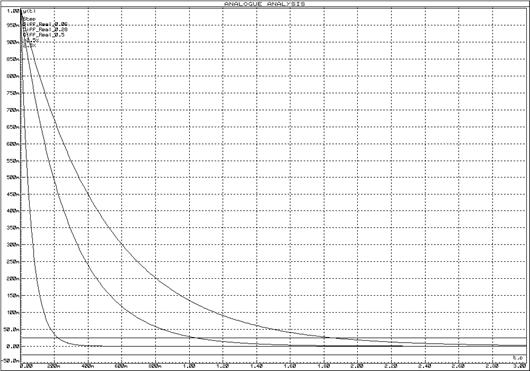
Рисунок 45 – Переходные функции реального дифференцирующего звена

d.   Реализация реального дифференцирующего звена

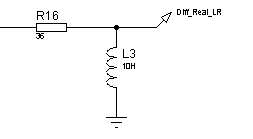
Реализуем реальное дифференцирующее звено с помощью схем, изображенных на рисунке 46. ЛАЧХ и ЛФЧХ дифференцирующего звена представлены на рисунках 47, переходные функции – на рисунке 48.

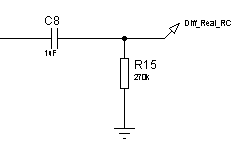
а)б)

а) -цепочка;б) -цепочка

Рисунок 46 – Электрические принципиальные схемы реального дифференцирующего звена

Рисунок 47 – ЛАЧХ и ЛФЧХ схем реализации дифференцирующего звена

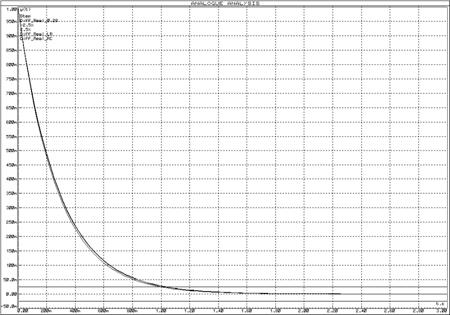
Рисунок 48 – Переходная функция схемы реального дифференцирующего звена

4.   Исследование интегрирующих звеньев

a.   Исследование частотных характеристик идеального интегрирующего звена

Для исследования частотных характеристик идеального интегрирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 49. Логарифмические частотные характеристики идеального интегрирующего звена представлены на рисунке 50, график переходной функции – на рисунке 51.

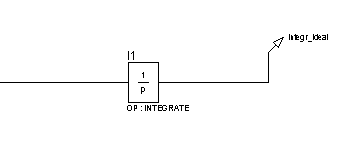
Рисунок 49 – Структурная схема для исследования идеального интегрирующего звена

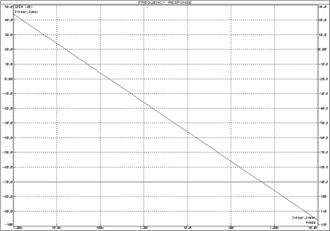
Рисунок 50 – Логарифмические частотные характеристики идеального интегрирующего звена

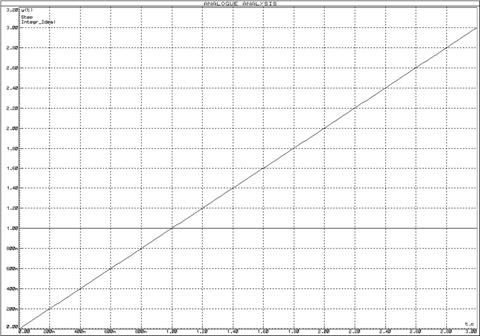
Рисунок 51 – Переходная функция идеального интегрирующего звена

b.   Реализация идеального интегрирующего звена

Реализуем идеальное интегрирующее звено схемой, изображенной на рисунке 52. ЛАЧХ и ЛФЧХ интегрирующего звена представлены на рисунках 53 и 54, переходная функция – на рисунке 55.

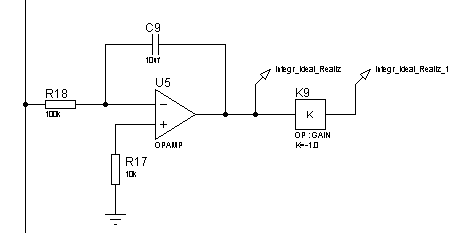
Рисунок 52 – Электрическая принципиальная схема интегрирующего звена

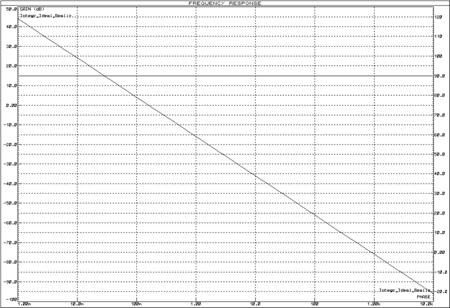
Рисунок 53 – ЛАЧХ и ЛФЧХ интегрирующего звена

Рисунок 54 – ЛАЧХ и ЛФЧХ интегрирующего звена с инвертором

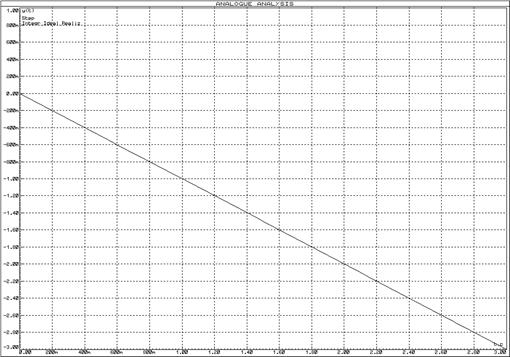
Рисунок 55 – Переходная функция схемы реализации идеального интегрирующего звена

c.    Исследование частотных характеристик реального интегрирующего звена

Для исследования частотных характеристик реального интегрирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 56. Логарифмические частотные характеристики реального интегрирующего звена представлены на рисунке 57, переходные функции – на рисунке 58.

Рисунок 56 – Структурная схема для исследования реального интегрирующего звена

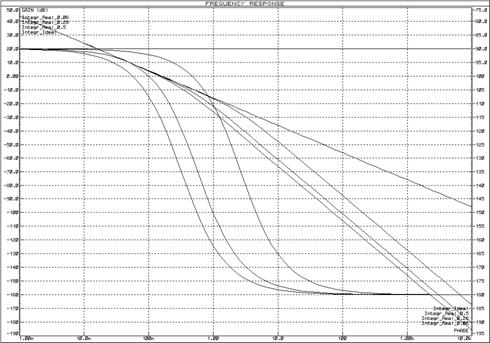
Рисунок 57 – Логарифмические частотные характеристики реального интегрирующего звена

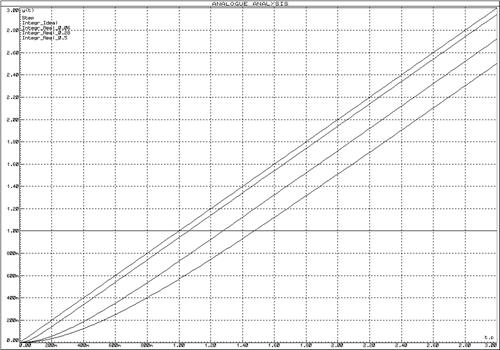
Рисунок 58 – Переходные функции реального интегрирующего звена

При анализе частотных и переходных характеристик реального интегрирующего звена и его реализации можно сделать следующие выводы:

5.   Исследование изодромного звена

Изодромное звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, - идеального интегрирующего и безынерционного. Поэтому данное звено совмещает полезные качества обоих звеньев и часто используется в качестве регулирующего устройства ПИ-регулятора (пропорционально-интегрального регулятора).

a.   Исследование частотных характеристик изодромного звена

Для исследования частотных характеристик изодромного звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 59. Логарифмические частотные характеристики изодромного звена представлены на рисунке 60.

Рисунок 59 – Структурная схема для исследования изодромного звена

Рисунок 60 – Логарифмические частотные характеристики изодромного звена

b.   Реализация изодромного звена

Реализуем изодромное звено схемой, изображенной на рисунке 61. ЛАЧХ и ЛФЧХ интегрирующего звена представлены на рисунках 62 и 63, переходная функция – на рисунке 64.

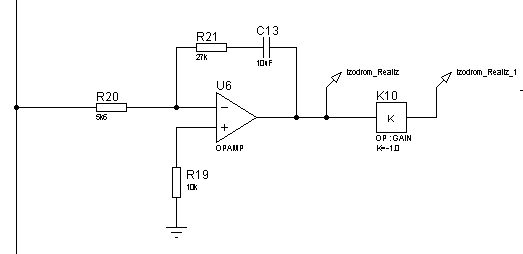
Рисунок 61 – Электрическая принципиальная схема изодромного звена

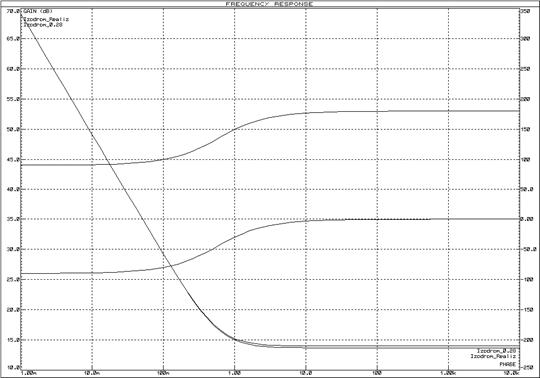
Рисунок 62 – ЛАЧХ и ЛФЧХ изодромного звена

Рисунок 63 – ЛАЧХ и ЛФЧХ изодромного звена с инвертором

а) б)

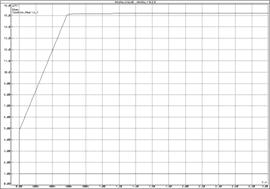
а) без инвертора;

б) с инвертором

Рисунок 64 – Переходная функция изодромного звена

6.   Исследование звена запаздывания

Для исследования частотных характеристик звена запаздывания в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 65. Логарифмические частотные характеристики изодромного звена представлены на рисунке 66, переходные характеристики – на рисунке 67.

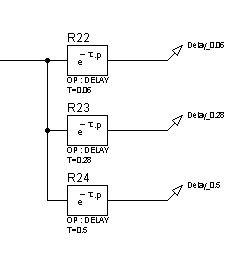
Рисунок 65 – Структурная схема для исследования звена запаздывания

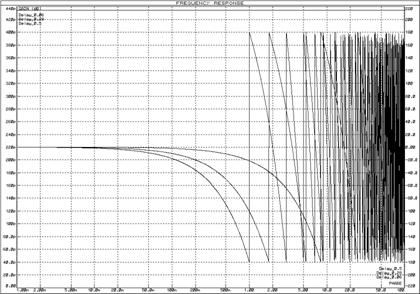
Рисунок 66 – Логарифмические частотные характеристики звена запаздывания

Рисунок 67 – Переходные функции звена запаздывания