Навигация
Типовые динамические звенья и их характеристики
Типовые динамические звенья и их характеристики
Динамическим звеном называется элемент системы, обладающий определенными динамическими свойствами.
Любую систему можно представить в виде ограниченного набора типовых элементарных звеньев, которые могут быть любой природы, конструкции и назначения. Передаточную функцию любой системы можно представить в виде дробно-рациональной функции:
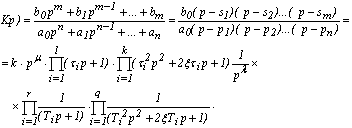 (1)
(1)
Таким образом, передаточную функцию любой системы можно представить как произведение простых множителей и простых дробей. Звенья, передаточные функции которых имеют вид простых множителей или простых дробей, называют типовыми или элементарными звеньями. Типовые звенья различаются по виду их передаточной функции, определяющей их статические и динамические свойства.
Как видно из разложения, можно выделить следующие звенья:
1. Усилительное (безынерционное).
2. Дифференцирующее.
3. Форсирующее звено 1-го порядка.
4. Форсирующее звено 2-го порядка.
5. Интегрирующее.
6. Апериодическое (инерционное).
7. Колебательное.
8. Запаздывающее.
При исследовании систем автоматического управления она представляется в виде совокупности элементов не по их функциональному назначению или физической природе, а по их динамическим свойствам. Для построения систем управления необходимо знание характеристик типовых звеньев. Основными характеристиками звеньев являются дифференциальное уравнение и передаточная функция.
Рассмотрим основные звенья и их характеристики.
Усилительное звено (безынерционное, пропорциональное). Усилительным называют звено, которое описывается уравнением:
![]() (2)
(2)
или передаточной функцией:
![]() (3)
(3)
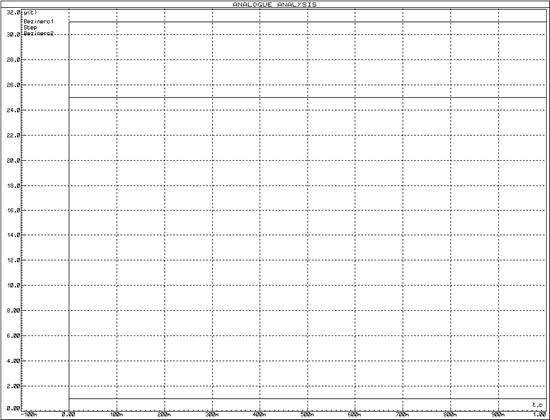
При этом переходная функция усилительного звена (рис. 1а) и его фун-кция веса (рис. 1б) соответственно имеют вид:
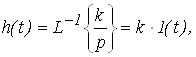
![]()
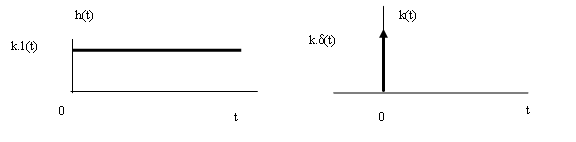
а) б)
Рис. 1
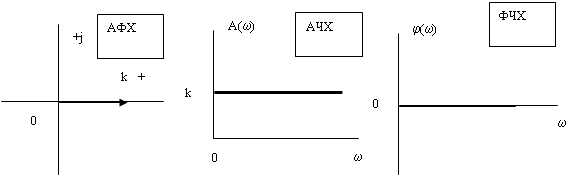
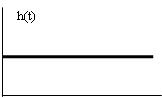
Частотные характеристики звена (рис. 2) можно получить по его передаточной функции, при этом АФХ, АЧХ и ФЧХ определяются следующими соотношениями:
![]() .
.
 | ||||
 | ||||
 | ||||
Рис. 2
Логарифмическая частотная характеристика усилительного звена (рис. 3) определяются соотношением ![]() .
.
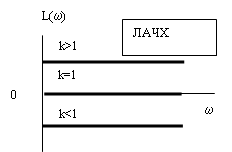
Рис. 3
Примеры звена:
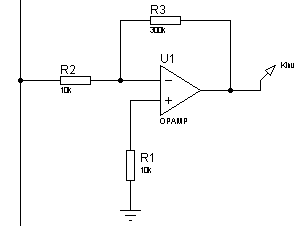
1. Усилители, например, постоянного тока (рис. 4а).
2. Потенциометр (рис. 4б).
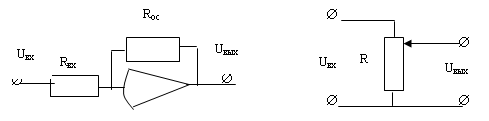
а) б)
Рис. 4
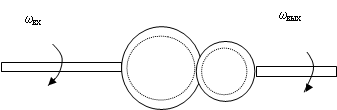
3. Редуктор (рис. 5).
 | |||
| |||
Рис. 5
Апериодическое (инерционное) звено. Апериодическим называют звено, которое описывается уравнением:
![]() (4)
(4)
или передаточной функцией:
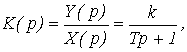 (5)
(5)
где Т – постоянная времени звена, которая характеризует его инерционность, k – коэффициент передачи.
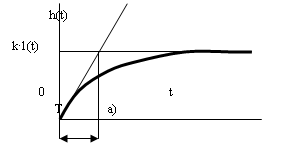
При этом переходная функция апериодического звена (рис. 6а) и его функция веса (рис. 6б) соответственно имеют вид:


 | |||||
 | |||||
| |||||
Рис. 6
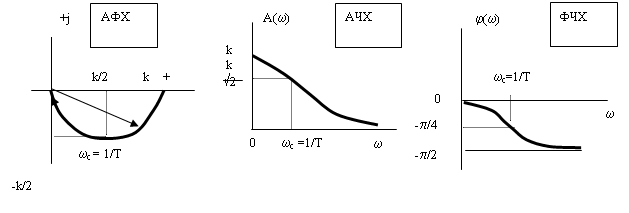
Частотные характеристики апериодического звена (рис. 7а-в) опреде-ляются соотношениями:
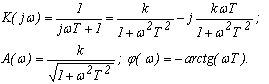
 | ||||
 | ||||
 | ||||
а) б) в)
Рис. 7
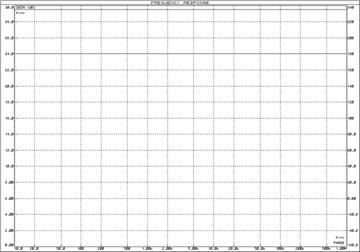
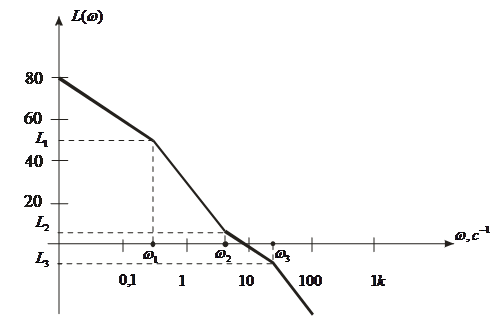
Логарифмические частотные характеристики звена (рис. 8) определяются по формуле
![]()
При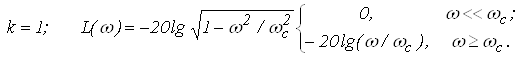
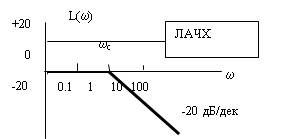
Рис. 8
Это асимптотические логарифмические характеристики, истинная характеристика совпадает с ней в области больших и малых частот, а максимальная погрешность будет в точке, соответствующей сопряженной частоте, и равна около 3 дБ. На практике обычно используют асимптотические характеристики. Их основное преимущество в том, что при изменении параметров системы (k и T) характеристики перемещаются параллельно самим себе.
Примеры звена:
Похожие работы
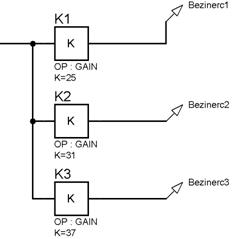
... прямую на ось , то это и будет сопрягающая частота. Постоянную времени можно определить, зная сопрягающую частоту : . c. Исследование частотных характеристик апериодического звена 2-го порядка Для исследования частотных характеристик апериодического звена 2-го порядка в прикладном пакете ProteusISIS составляем структурную схему, представленную на рисунке 16, при неизменной первой постоянной ...
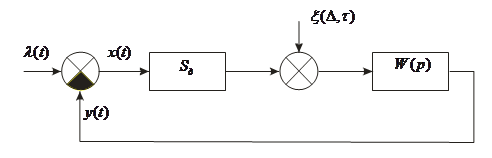
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
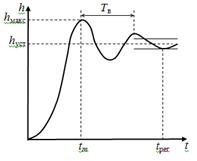
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
... 61508;Х=Хвх+-Хо.с. и решив их совместно получим ур-е W=Wпр/(1+-Wпр*Wо.с.) Структурные методы широко используются в инженерной практике для характеристики процессов в элементах и системах автоматики Структурные схемы элементов автоматических систем формируются на основе совокупности ур-ий, которые связывают характеристики процесса с параметрами и начальными условиями этого процесса в сочетании с ...
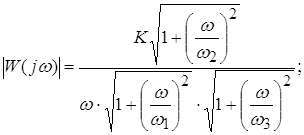
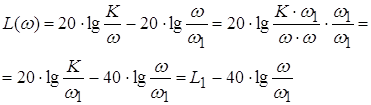
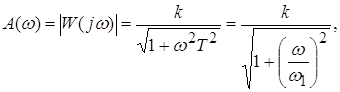

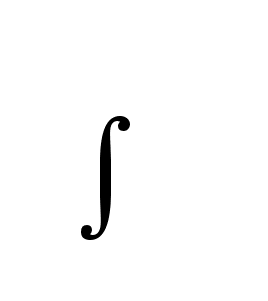
0 комментариев