Навигация
Определение ускорений звеньев механизмов иглы и нитепритягивателя и построение плана ускорений
3 Определение ускорений звеньев механизмов иглы и нитепритягивателя и построение плана ускорений
 (16)
(16)
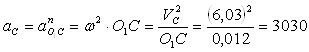 (17)
(17)
При ω=const касательная составляющая ускорений ![]() = 0,
= 0, ![]() = 0.
= 0.
Для построения плана ускорений выбирается масштаб ускорений Ka, м/(с2*мм), который рассчитывается как:
Ka = ![]() (18)
(18)
Из произвольно выбранной точки - полюса плана ускорений откладывают (Ра) - откладывают вектор ac = ![]() направленный по линии CO1 к полюсу вращения О1 . В результате на плане ускорений получают точку с, к которой направлен вектор aoC = ac .
направленный по линии CO1 к полюсу вращения О1 . В результате на плане ускорений получают точку с, к которой направлен вектор aoC = ac .
Линейное ускорение точки D определяют путем решения следующих векторных уравнений:
 , (19)
, (19)
![]() где a02 = 0 (точка О2 неподвижна).
где a02 = 0 (точка О2 неподвижна).
Величины нормальных составляющих ускорений, входящих в систему уравнений (19) определяют по формулам:
![]() =
= ![]() =
=  =
=  ;
(20)
;
(20)
![]() =
= ![]() (21)
(21)
![]()
![]()
![]()
Векторы касательных составляющих ускорений, входящих в систему уравнений (10) на плане ускорений направляют следующим образом:
![]()
В соответствии с уравнением (10) из конца вектора ![]() , т.е. точки с, на плане ускорений проводят вектор
, т.е. точки с, на плане ускорений проводят вектор ![]() параллельно линии CD в направлении от точки D к полюсу вращения – точке С (вниз). Далее из конца вектора
параллельно линии CD в направлении от точки D к полюсу вращения – точке С (вниз). Далее из конца вектора ![]() проводят перпендикуляр – линию действия
проводят перпендикуляр – линию действия ![]() .
.
Во втором векторном уравнении (10) вектор ![]() , поэтому из полюса ускорений
, поэтому из полюса ускорений ![]() проводят вектор
проводят вектор ![]() параллельно линии
параллельно линии ![]() в направлении от точки
в направлении от точки ![]() к точке
к точке ![]() (влево). Из конца этого вектора проводят перпендикуляр к нему – линию действия
(влево). Из конца этого вектора проводят перпендикуляр к нему – линию действия ![]() . Пересечение линий действий касательных ускорений определяет положение точки d на плане ускорений.
. Пересечение линий действий касательных ускорений определяет положение точки d на плане ускорений.
Соединив полюс плана ускорений точку ![]() с точкой d, получают вектор ускорения
с точкой d, получают вектор ускорения ![]() . При этом все ранее построенные векторы направлены к точке d.
. При этом все ранее построенные векторы направлены к точке d.
Теорема подобия справедлива и для плана ускорений. Поэтому значительно проще найти положение точки е на плане ускорений, построив от линии cd треугольник cde, подобный треугольнику CDE на схеме механизма и сходственно с ним расположенный.
Для нанесения на план ускорений точки е можно использовать метод засечек так же, как и при построении плана скоростей. Для этого соответственно из точек d и c в нужном направлении делают засечки дуг радиусами, равными длине векторов ![]() и
и ![]() , мм:
, мм:
![]() (22)
(22)
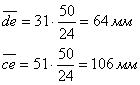
На следующем этапе кинематического анализа из полюса плана ускорений ![]() откладывают вектор
откладывают вектор ![]() направленный по линии ОА1 к полюсу вращения О1. В результате на плане ускорений получают точку а, к которой направлен вектор
направленный по линии ОА1 к полюсу вращения О1. В результате на плане ускорений получают точку а, к которой направлен вектор ![]() .
.
Линейное ускорение точки В определяют путем решения следующих векторных уравнений:
 (23)
(23)
где ![]() =0 (точка О1 неподвижна).
=0 (точка О1 неподвижна).
Вектор нормальный составляющей ускорения ![]() , входящей в систему уравнений (23) определяют по формулам:
, входящей в систему уравнений (23) определяют по формулам:
 . (24)
. (24)
![]()
Вектор касательной составляющей ускорения ![]() , входящих в систему уравнений (23) на плане ускорений направляют следующим образом:
, входящих в систему уравнений (23) на плане ускорений направляют следующим образом: ![]() .
.
В соответствии с уравнениями (14) из конца вектора ![]() , т.е. точки а, на плане ускорений проводят вектор
, т.е. точки а, на плане ускорений проводят вектор ![]() параллельно линии АВ в направлении к полюсу вращения – точке
параллельно линии АВ в направлении к полюсу вращения – точке ![]() . Далее из конца вектора
. Далее из конца вектора ![]() проводят перпендикуляр – линию действия
проводят перпендикуляр – линию действия ![]() .
.
Во втором векторном уравнении (14) вектор ![]() , поэтому из полюса ускорений
, поэтому из полюса ускорений ![]() проводят вектор
проводят вектор ![]() параллельно линии
параллельно линии ![]() в направлении к точке
в направлении к точке ![]() . Пересечение линий действий касательного ускорения
. Пересечение линий действий касательного ускорения ![]() и ускорения
и ускорения ![]() определяет положение точки в на плане ускорений.
определяет положение точки в на плане ускорений.
Для нанесения на план ускорений точек центров тяжести, можно воспользоваться теоремой подобия. Например, для точки ![]() - центра тяжести звена 5 – можно составить пропорцию:
- центра тяжести звена 5 – можно составить пропорцию:
![]() (25)
(25)
и полученный отрезок отложить из полюса ![]() по направлению к точке
по направлению к точке ![]() .
.
План ускорений позволяет определить линейное ускорение любой точки на всяком звене, ![]() , используя следующие формулы:
, используя следующие формулы:
 (26)
(26)
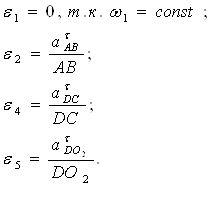
Построив план линейных ускорений, можно определить угловые ускорения, ![]() , звеньев механизма:
, звеньев механизма:
 (27)
(27)
Таблица 3: данные для построения ускорений механизмов иглы и нитепритягивателя
|
|
|
|
|
| |
| 11 | 0,54 | 3,4 | 64 | 106 | 0,028 |
| 1 | 2,9 | 1,9 | 43 | 70 | 0,058 |
| 2 | 45,4 | 2 | 64 | 106 | 0,008 |
Похожие работы
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
0 комментариев