Навигация
Разработка алгоритма управления и расчет параметров элементов структурной схемы
3. Разработка алгоритма управления и расчет параметров элементов структурной схемы
Согласно эквивалентной схеме замещения запишем следующие дифференциальные уравнения:
![]()
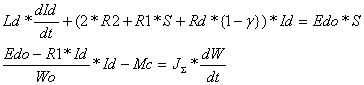
где: ![]()
Данный объект нелинейный, т.к. присутствуют g*Id, Id2 и т.д. Рассмотрим линеаризацию объекта, и запишем уравнения в приращениях:
![]()
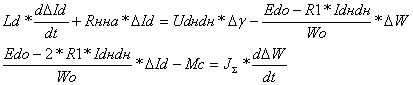
где: ![]()
![]() .
.
Целесообразно использовать двухконтурную систему подчиненного регулирования координат с внутренним контуром выпрямленного тока. Исходя из линеаризованных дифференциальных уравнений, получим следующую структуру (рис.3):
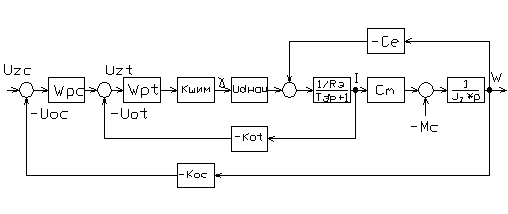
рис.3
Данная структура представлена в общем виде. Определяем параметры объектов: Рассчитаем максимальную электромагнитную постоянную времени и минимальную электромеханическую постоянную, и определим их соотношение:
![]()
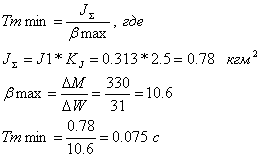
Найдем отношение постоянных времени:
![]()
Т.к. отношение m>>8, следовательно, при расчетах мы можем пренебречь влиянием обратной связи по ЭДС двигателя.
Для определения коэффициентов двигателя Се и См рассчитаем значение Idнач из формулы:
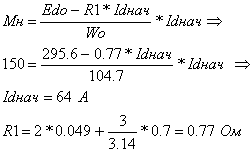
Для найденного значения Idнач рассчитаем коэффициенты Се и См по формулам:
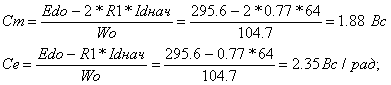
Определим значение эквивалентного сопротивления:
![]() ;
;
примем среднее значение![]() =0.5, S=0.95 Þ
=0.5, S=0.95 Þ
![]()
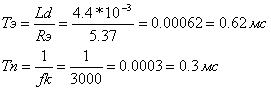
Т.к. эквивалентная электромагнитная постоянная времени соизмерима с постоянной времени преобразователя, то мы не можем пренебречь дискретностью преобразователя. Для искусственного увеличения Тэ введем в цепь ротора дополнительный реактор с индуктивностью Ld’=6 мГн.
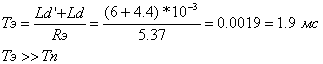 Þ
Þ
Дискретность широтно-импульсного преобразователя можно не учитывать. Коэффициент передачи ШИМ примем равным Кшим=1.
![]()
Произведем настройку контура тока на технический оптимум. Рассчитаем необходимый регулятор тока:
![]()
за малую постоянную времени примем:![]()
Кot – коэффициент обратной связи по току Id.
![]()
![]() ;
;
итак, получили ПИ – регулятор тока, с постоянной Тpt=0.059.
Передаточную функцию замкнутого контура тока представим в виде:
![]()
Контур скорости также настроим на технический оптимум:
![]() ;
;
Кос – коэффициент обратной связи по скорости
![]()
![]()
Мы получили П – регулятор скорости Крс=22
4. Расчет динамических характеристик
Расчет динамических характеристик проведем с помощью комплекса МИК-АЛ, используя структуру на рис.3 (но с учетом упругой механической части). Ниже приведена программа моделирования данного объекта:
$Ввод *kurs
КОНСТ
Uu=1,Mc=10.3,Kрc=22,Tрт=0.059,Kшим=1,Udn=509.44,L=0.0104,
J1=0.78,Koc=0.147,Kот=0.156
17V V=Uu
111U W=1 Вх=17
1U W=Kрc Вх=111+15
2N огран пар=10 Вх=1
3L W=1/Tрт*p Вх=2+16
4N огран пар=10 Вх=3
5U W=Kшим Вх=4
6U W=Udn Вх=5
7L W=1/L*p Вх=6+100+200
*Cm*
21U W=1.05 Вх=7
*Ce*
100U W=-1.85 Вх=9
*R*
200U W=-40.6 Вх=7
9L W=1/J1*p Вх=21+14
14V V=-Mc
15U W=-Koc Вх=9
16U W=-Kот Вх=7
Инт RKT4
Нач вр=0
Кон вр=0.65
Шаг инт=0.0001
шаг выв=0.001
Вывод 7,21,9
Выходы 7=I,21=M,9=w1
Диспл 7,21,9
$Кон
$Стоп
Результаты моделирования представлены в виде графиков:
1.Пуск на минимальную скорость при минимальном моменте сопротивления (Uy=1, Mc=30 Нм)
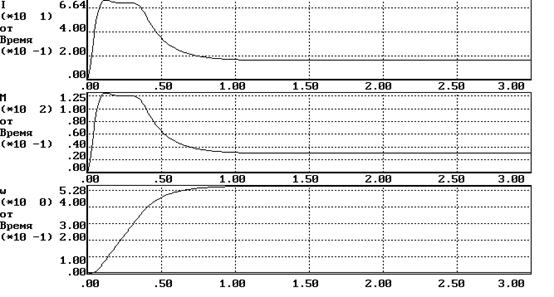
Время регулирования (время вхождения в пятипроцентный коридор) tр=0.2 с;
Перерегулирование s=0.2%;
Ошибка DWуст=0.038рад (DWмах=0.0524 рад)
2.Пуск на минимальную скорость при максимальном моменте сопротивления (Uy=1, Mc=150 Нм)
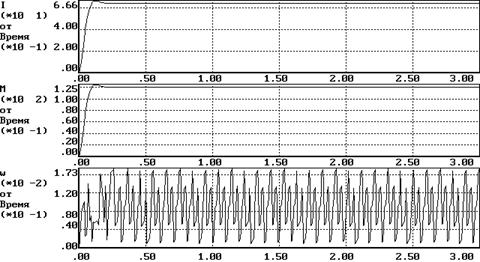
3.Пуск на максимальную скорость при минимальном моменте сопротивления (Uy=10, Mc=30 Нм)
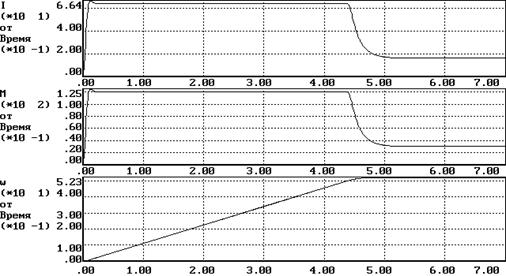
Время регулирования (время вхождения в пятипроцентный коридор) tр=0.5 с;
Перерегулирование s=1%
Ошибка DWуст=0.41рад (DWмах=0.52 рад);
4.Пуск на максимальную скорость при максимальном моменте сопротивления (Uy=10, Mc=150 Нм)
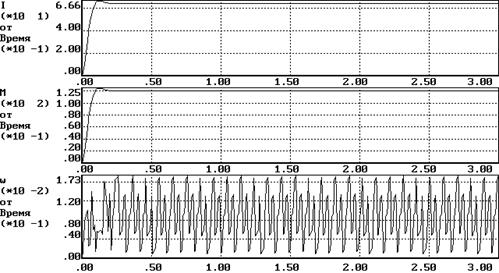
Как видно из приведенных графиков, результаты не только не удовлетворяют техническому заданию, но и смоделированная структура не отражает в полном объеме свойств системы.
Заменим в структуре постоянные коэффициенты См, Се, R на переменные, в соответствии со следующими формулами:
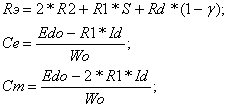 ,где S, g, Id – переменные.
,где S, g, Id – переменные.
Для улучшения свойств системы, введем адаптивный регулятор с эталонной моделью, формирующей оценку управляющей координаты при настройке контура на технический оптимум с постоянной времени Тm=0.002 с.
Передаточная функция эталонной модели составляет два последовательно соединенных звена ![]() ,
, ![]() , охваченных отрицательной единичной обратной связью. Передаточная функция замкнутого контура ЭМ имеет вид:
, охваченных отрицательной единичной обратной связью. Передаточная функция замкнутого контура ЭМ имеет вид:
![]()
Суммарная структурная схема представлена на рис.4.
В процессе моделирования экспериментально подбираем значения следующих коэффициентов:
Коэффициент П - регулятора скорости (Крс=10),
Коэффициент усиления адаптивного регулятора (Kку=30).
Листинг модели.
$ввод
*kurs
конст Uu=1,Mc=150,Krs=10,Trt=0.059,Ksh=1,Udn=509.44,L=0.0104,
J1=0.78,Koc=0.147,Kot=0.156,R1=0.77,
R2=0.33,Edo=295.6,Rd=7.96
17V V=Uu
111U W=1 bx=17
555l W=1/0.000008p2+0.004p+1 en=111
557U W=30 en=555+558
558U W=-0.147 en=9
1U W=Krs bx=111+15
2N огран пар=10 bx=1+557
3L W=1/Trt*p bx=2+16
4N огран пар=10 bx=3
5U W=Ksh bx=4
6U W=Udn bx=5
7L W=1/L*p bx=6+100+200
*Cm*
8U W=-2*R1 bx=7
20V V=Edo
1111U W=0.00955 bx=7+20
21N умн bx=1111+7
*21U W=1.88 bx=7
*Ce*
22U W=-R1 bx=7
23V V=Edo
24U W=0.00955 bx=22+23
99N умн bx=24+9
100U W=-1 bx=99
*100U W=-2.35 bx=9
*R*
25U W=-1 bx=5 *gamma*
26V V=1
27U W=Rd bx=26+25 *Rd*(1-gamma)*
28V V=2*R2
29U W=-1 bx=9 *-W1*
30V V=104.7
31U W=0.00955 bx=30+29 *S*
125U W=2*R1 bx=31
199U W=-1 bx=125+27+28 *-R*
200N умн bx=199+7
*200U W=-5.37 bx=7
9L W=1/J1*p bx=21+18
15U W=-Koc bx=9
16U W=-Kot bx=7
32N реле пар=Mc bx=9
18U W=-1 bx=32
инт RKT4
нач вр=0
кон вр=0.3
шаг инт=0.0001
шаг выв=0.001
вывод 7,21,9
выходы 7=I,21=M,9=w
диспл 7,21,9
$кон
$стоп
Ниже приведены результаты моделирования. Как видно из графиков, спроектированная система практически полностью удовлетворяет требованиям технического задания.
1.Пуск на минимальную скорость при минимальном моменте сопротивления (Uy=1, Mc=30 Нм)
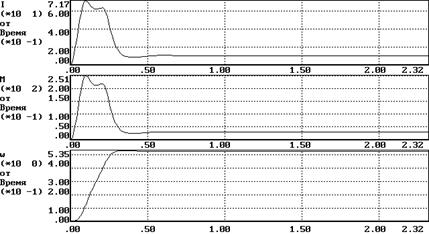
Время регулирования (время вхождения в пятипроцентный коридор) tр=0.06 с;
Перерегулирование s=1.5% ;
Ошибка DWуст=0.035рад (DWмах=0.0525 рад);
2.Пуск на минимальную скорость при максимальном моменте сопротивления (Uy=1, Mc=150 Нм)
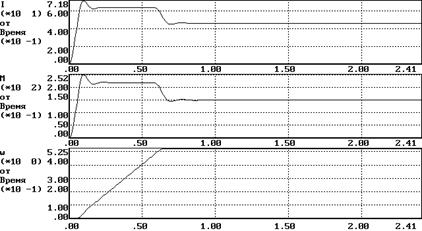
Время регулирования (время вхождения в пятипроцентный коридор) tр=0.067 с;
Перерегулирование s=1% ;Ошибка DWуст=0.01рад (DWмах=0.0525 рад);
3.Пуск на максимальную скорость при минимальном моменте сопротивления (Uy=10, Mc=30 Нм)
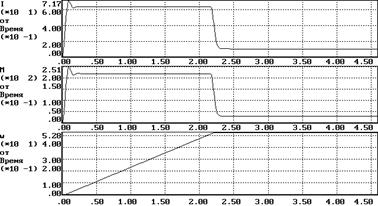
Время регулирования (время вхождения в пятипроцентный коридор) tр=0.23 с;
Перерегулирование s=0.1% ;
Ошибка DWуст=0.4рад (DWмах=0.525 рад)
4.Пуск на максимальную скорость при максимальном моменте сопротивления (Uy=10, Mc=150 Нм)
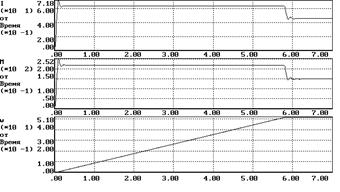
Время регулирования (время вхождения в пятипроцентный коридор)tр=0.61 с;
Перерегулирование s=0.3%;
Ошибка DWуст=0.45 рад (DWмах=0.525 рад);
0 комментариев