Навигация
Расчет частотных характеристик фильтра
3. Расчет частотных характеристик фильтра
Уравнение комплексной передаточной функции ![]() может быть получено из уравнения операторной передаточной функции
может быть получено из уравнения операторной передаточной функции ![]() при замене операторной переменной
при замене операторной переменной ![]() на мнимую частоту
на мнимую частоту ![]() :
:
![]() =
=![]() .
.
В свою очередь, после выделения действительных ![]() ,
, ![]() и мнимых
и мнимых ![]() ,
, ![]() составляющих числителя
составляющих числителя ![]() и знаменателя
и знаменателя ![]() дробного выражения комплексной передаточной функции
дробного выражения комплексной передаточной функции
![]() =
=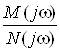 =
=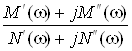 ,
,
легко находятся уравнения АЧХ и ФЧХ цепи:
![]() =
= =
=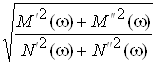 ;
;
![]() =
=![]() =
=![]() -
-![]() ;
;
![]() =
=![]() при
при ![]() ;
;
![]() =
=![]() при
при ![]() ,
, ![]() ;
;
![]() =
=![]() при
при ![]() ,
, ![]() ;
;
![]() =
=![]() при
при ![]() ;
;
![]() =
=![]() при
при ![]() ,
, ![]() ;
;
![]() =
=![]() при
при ![]() ,
, ![]() .
.
Уравнения АЧХ и ФЧХ фильтра получим из дробно-рационального выражения его операторной функции передачи:
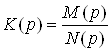 =
=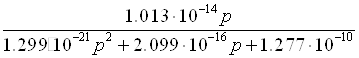
Положив ![]() =
=![]() , получим выражение для комплексной передаточной функции:
, получим выражение для комплексной передаточной функции:
![]() =
=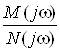 =
=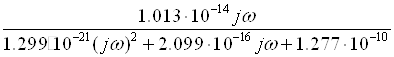 =
=
=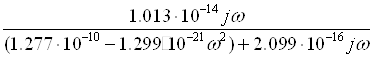
Определив модуль этого комплексного выражения, найдем уравнение АЧХ фильтра:
![]() =
=![]() =
= =
=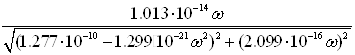
Для нахождения уравнения ФЧХ нужно найти аргумент функции ![]() :
:
![]() =
=![]() =
=![]() =
=![]() -
-![]() .
.
Оставаясь действительным, полином числителя
![]() =
=![]()
при любой частоте не меняет свой знак. Поэтому ![]() =0 при любой
=0 при любой![]() (
(![]() ≥0).
≥0).
У полинома знаменателя
![]() =
= ![]()
действительная часть
![]() =
=![]()
при частоте ω>313538 рад\с меняет знак. В зависимости от знака действительной части аргумент комплексной функции будет определяться по разным формулам:
![]() =
=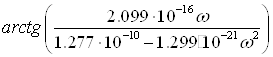
при 0≤![]() <313538 рад/с (
<313538 рад/с (![]() >0);
>0);
![]() =
= 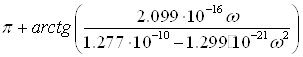
при ![]() ≥313538 рад/с (
≥313538 рад/с (![]() <0).
<0).
![]() =
=![]()
при ![]() =313538 рад/с
=313538 рад/с
Таким образом, уравнение ФЧХ будет выглядеть следующим образом
![]() =-
=-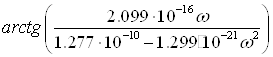
при 0≤![]() <313538рад/с
<313538рад/с
![]() =
=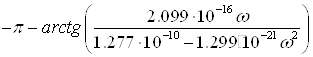
при ![]() >313538рад/с
>313538рад/с
![]() =
=![]()
при ![]() =313538 рад/с
=313538 рад/с
По полученным уравнениям (задавая с определенным шагом значения ![]() и вычисляя соответствующие значения
и вычисляя соответствующие значения ![]() =2π
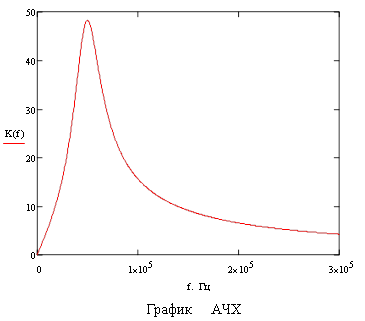
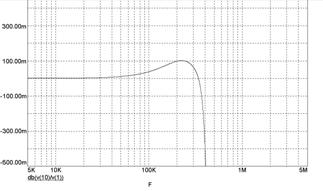
=2π![]() ) можно построить графики АЧХ
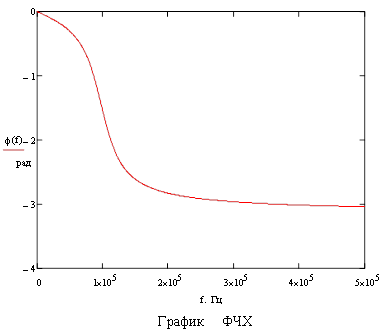
) можно построить графики АЧХ ![]() и ФЧХ
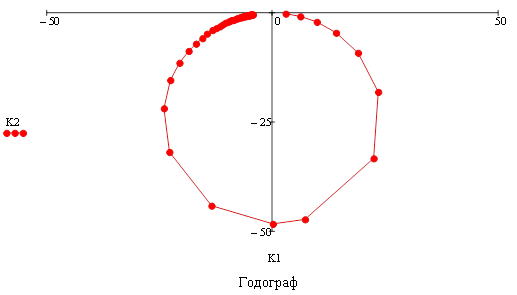
и ФЧХ ![]() фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU(jf)=K(ω)ехр(jφ(f)), а алгебраической КU(jf)=A(f)+jB(f)=K(f)cosφ(f) + j K(f)sinφ(f).
фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU(jf)=K(ω)ехр(jφ(f)), а алгебраической КU(jf)=A(f)+jB(f)=K(f)cosφ(f) + j K(f)sinφ(f).
По графику определим частоту среза ![]() полосу пропускания
полосу пропускания ![]() , крутизну спада амплитудно-частотной характеристики
, крутизну спада амплитудно-частотной характеристики ![]() :
:
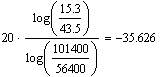

![]() Дб/дек
Дб/дек ![]() Дб/дек
Дб/дек
![]() н=39300 Гц
н=39300 Гц
![]() н=63300Гц
н=63300Гц
![]() →63300-39300=24000Гц
→63300-39300=24000Гц
Расчет частотных характеристик всегда проводят в определенном диапазоне частот, в котором проявляются основные частотные свойства электрической цепи. Величину диапазона частот можно определить по полюсно-нулевой карте операторной функции.
В качестве нижней граничной частоты fн можно принять значение, близкое к величине
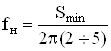
где Smin – расстояние от начала координат до ближайшей особой точки (нуля или полюса)
Это расстояние определяется как модуль особой точки: S =p0или S=p*.
За верхнюю граничную частоту fв можно взять значение
![]()
где Smax – расстояние от начала координат до самой удаленной особой точки. Рассчитаем граничные частоты для нашего примера.
p0=0 рад/c, ![]()
Следовательно, Smin=p0, Smax=p*,
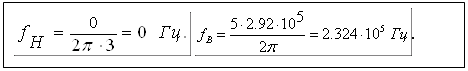
Похожие работы
... минимизация (53) становится доминирующей, а условие (55) – желаемым. 6. Базовый алгоритм структурного синтеза схем с собственной компенсацией Выполненные исследования указывают на существование двух принципов собственной компенсации влияния параметров активных элементов на характеристики электронных устройств различного функционального назначения. Создание компенсирующих контуров предполагает ...
... . Главным этапом при расчёте ЛЗ является конструирование передаточной функции, удовлетворяющей заданным требованиям. После этого осуществляется выбор схемы реализации и расчёт элементов цепи. 2. Линии задержки на фазовых звеньях У этого типа ЛЗ полностью снимается проблема АЧХ. Действительно, ОПФ фазового звена имеет вид Следовательно, Решая задачу синтеза ЛЗ на ...
... нелинейного преобразователя при наличии разделительного конденсатора рассчитывается: где Rк – сопротивление нагрузки, Rк=300Ом. Спектры амплитуд тока и напряжения приведены на Рис.11. 4. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ. Для выделения колебаний заданных частот необходимо рассчитать полосовые фильтры, у частотных характеристик которых центры эффективного пропускания совпадали ...
... : Наукова думка, 2010. – 205 с. 4. Лурье, О.Б. Интегральные микросхемы в усилительных устройствах [Текст] / О.Б. Лурье. – М. : Радио и связь, 2008. – 175 с. 5. Лыпарь, Ю.И. Проектирование оптимальных структур активных RC-фильтров [Текст] / Ю.И. Лыпарь, Д.А. Скобейка // Избирательные системы с обратной связью. – 2007. – Вып. 6. – С. 141. 6. Лыпарь, Ю.И. Структурный синтез электронных цепей [ ...




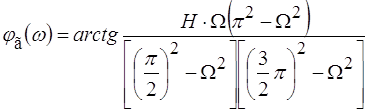


0 комментариев