Навигация
Передаточная функция фильтра
2.2 Передаточная функция фильтра
Рассчитываем передаточную функцию нормированного ФНЧ по формуле W(р)=N(р)/D(p). Находим полиномы N(р) и D(p) из таблиц [1] для фильтра Чебышева II порядка, учитывая, что пульсации в полосе пропускания равны 3 Дб. Получаем:
 (2.2)
(2.2)
Сделаем обратный переход от нормированного ФНЧ к проектируемому, для чего преобразуем передаточную функцию: W1(р)=N1(р)/D1(p), где
![]() (2.3)
(2.3)
Масштабируем по частоте: делаем замену р®wп/р, где wп =2p¦п=400p=1256,64 [рад/с]. Тогда D1(p)= D(wп/р) и передаточная функция примет вид:
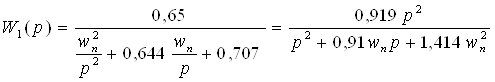 (2.4)
(2.4)
2.3 Выбор схемного решения
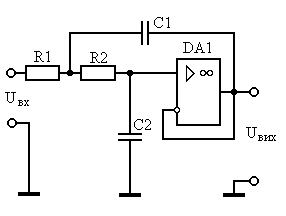
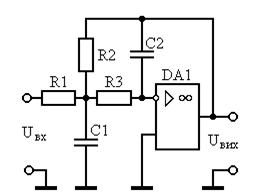
В соответствии с техническим заданием и рассчитанными параметрами, в качестве схемного решения выбираем ФВЧ-ІІ Саллена-Кея, так как схема имеет небольшой диапазон номиналов элементов. Порядок всего фильтра n=2 совпадает с порядком звена Саллена-Кея, поэтому для построения фильтра необходимо одно звено.
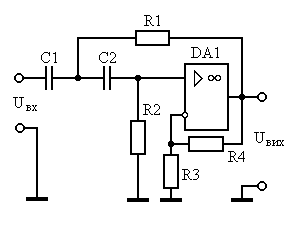
Рисунок 2.2 – ФВЧ-ІІ Саллена-Кея
3. Топологическая модель и расчет элементов фильтра
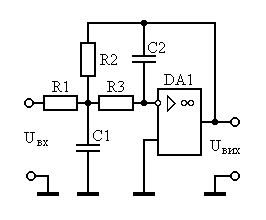
3.1 Граф Мезона ФВЧ- ІІ.
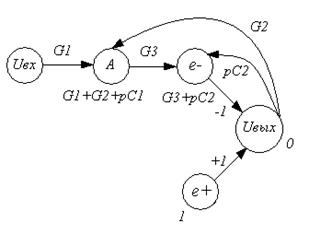
Составим граф Мезона для выбранной схемы.
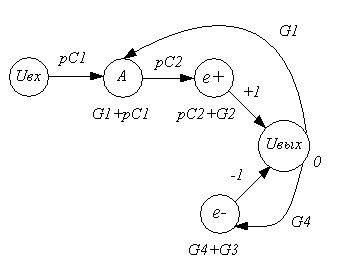
Рисунок 3.1 – Граф Мезона ФВЧ-ІІ
Найдём передаточную функцию по формуле Мезона:
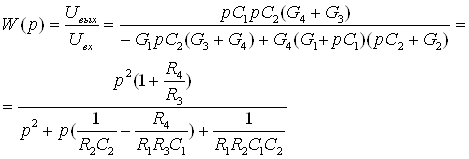 (3.1)
(3.1)
Сопоставим с канонической формулой для ФВЧ-ІІ [2]:
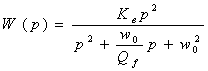 (3.2)
(3.2)
Откуда получим:
![]()
![]()
![]()
3.2 Расчет элементов схемы
Задаём ёмкость конденсаторов C1=C2=10/fn=10/0,2=50 (нФ)
Определяем сопротивление резисторов:
![]() (3.3)
(3.3)
Выбираем сопротивление R3=30 кОм, а R4 рассчитаем из соотношения:
![]() (3.4)
(3.4)
Согласуем номиналы элементов со стандартным рядом E6:
R1=R2=15 кОм; R4=37,4 кОм;
Устанавливаем в схему рассчитанные значения и снимаем АЧХ фильтра.
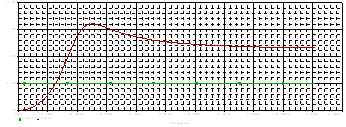
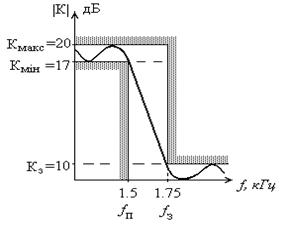
Рисунок 3.1 – АЧХ проектируемого фильтра
4. Методика настройки и регулировки фильтра
Коэффициент усиления фильтра можно настроить при помощи резисторов R3 и R4 [2]:
K=1+R4/R3; (4.1)
При использованном в схеме операционном усилителе, сопротивление резистора R3 можно выбирать в пределах от нескольких кОм до 1 Мом. При меньшем значении R3 становится большим ток, потребляемый схемой, а при большем – вносит своё влияние входное сопротивление микросхемы.
Сопротивление R4 определяется из формулы 4.1 для требуемого коэффициента усиления. Учитывая следующее соотношение (см. раздел 3.2):
![]() (4.2)
(4.2)
можно показать, что максимально достижимый коэффициент усиления в полосе пропускания равен 3. В этом случае добротность фильтра наибольшая, но при этом присутствуют наибольшие пульсации в полосе пропускания. При попытке увеличения Кл фильтр самовозбуждается и превращается в генератор колебаний на частоте w0. Из этого ограничения определим, что сопротивление R4 лежит в диапазоне от 0 до 2R3. При нулевом сопротивлении схема становится фильтром Баттерворта с единичным усилением.
Частоту w0 можно настроить с помощью элементов R1, R2, C1 и С2 [2]:
 (4.3)
(4.3)
При условии, что R1=R2=R и C1=C2=C, формула 4.3 упрощается: w0=1/RC. Если сопротивления и ёмкости не равны, то соотношением R1 к R2 и C1 к C2 регулируется добротность фильтра. При этом также нужно учитывать, что при больших добротностях фильтр склонен к самовозбуждению.
Выводы
В данной курсовой работе был разработан фильтр высокой частоты второго порядка с аппроксимацией полиномом Чебышева. Он состоит из одного звена Саллена-Кея 2 порядка. Устройство обеспечивает максимальный коэффициент усиления 3,2 в полосе пропускания. Частота полосы пропускания fn=180 кГц, что на 10% отличается от заданной. Это обусловлено использованием элементов из стандартного ряда E6, которые имеют разброс номиналов 10%. Фильтр допускает простую настройку коэффициента усиления и частоты пропускания, а также имеет небольшой разброс номиналов элементов. Из недостатков можно назвать наличие пульсаций в полосе пропускания, присущее фильтрам с аппроксимацией Чебышева.
Перечень ссылок
1. Методические указания к выполнению курсового проекта по дисциплине «Аналоговые электронные устройства» для студентов дневной и заочной формы обучения специальностей направления «Радиотехника» / Составители: Тимошенко Л.П., Басецкий В.Л., Х.: ХНУРЭ, 2001.
2. Зеленин А.Н, Костромицкий А.И, Бондарь Д.В. Активные фильтры на операционных усилителях. – Х.: Телетех, 2000. - 136 с.
3. Ногин В.Н. Аналоговые электронные устройства: Учеб. пособие для вузов. – М.: Радио и связь, 1992. – 309 с.
Похожие работы
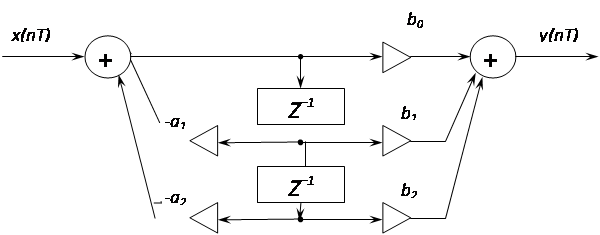
... , b2i , a2i определяют характеристики фильтра. При значениях коэффициентов фильтр имеет АЧХ фильтра верхних частот b 20 = 1;b 21 = 0;b 22 = 1.1; a 21 = 0.999;a 22 = 0.000 Разностное уравнение задает во временной области порядок получения выходной последовательности отсчетов из входной. В z-плоскости свойства цифрового фильтра описывает передаточная функция H(z), которая при двухкаскадной ...
... соединения ФНЧ- ІІ, как на рис. 2.2: Рисунок 2.2 – Структурная схема графа Мезона Выбор схемного решения Схемным решением для данного устройства будет фильтр низкой частоты второго порядка с многопетлевой обратной связью, т.к. он обеспечивает небольшую чувствительность к отклонению номиналов элементов. Используем 3 таких звена, соединённых последовательно. Рисунок 2.3 – ФНЧ-ІІ с ...
... доступны. 5. Низкочастотные фильтры можно построить на элементах малых номиналов. Целью данной курсовой работы является проектирование активного фильтра высоких частот основанного на интегральных операционных усилителях. 1. Существующие виды активных ВЧ фильтров Рассмотрим методы реализации различных типов функций цепи, основанные на использовании схем фильтров, включающих как активные, ...
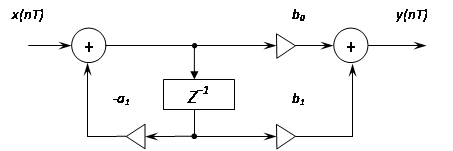
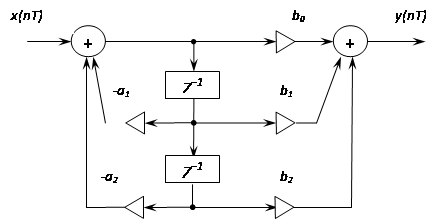
... звеньев первого и второго порядка представлена на следующем рисунке: 3. Методы расчета БИХ-фильтров и вид целевой функции Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях. ...



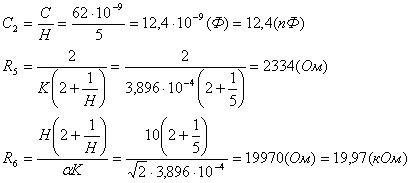
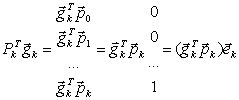
0 комментариев