Навигация
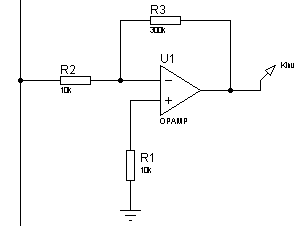
Дифференцирующее звено может быть реализовано на операционных усилителях (рис. 19)
1. Дифференцирующее звено может быть реализовано на операционных усилителях (рис. 19).
 | |||
 |
Æ Æ
Рис. 19
2. Тахогенератор (рис. 20).
 Æ
Æ
|
Æ
Рис. 20
Колебательное звено. Колебательным называют звено, которое описывается уравнением:
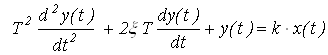 (10)
(10)
или передаточной функцией:
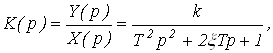 (11)
(11)
где x – демпфирование (0 £ x £ 1).
Если x = 0, то демпфирование отсутствует (консервативное звено – без потерь), если x = 1, то имеем два апериодических звена.
При этом переходная функция звена и его функция веса (рис. 21) соответственно имеют вид:
 (12)
(12)
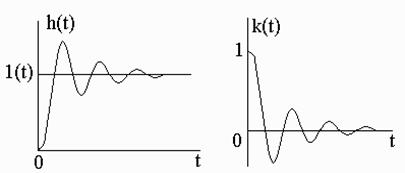 |
а) б)
Рис. 21
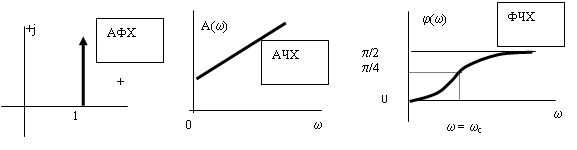
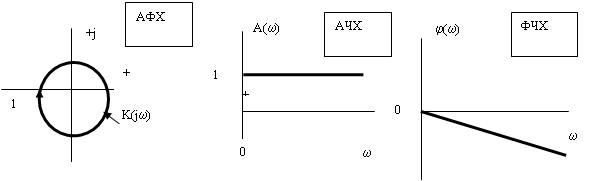
Амплитудно-фазовая частотная характеристика (АФХ) имеет вид (рис. 22а) и определяется соотношением
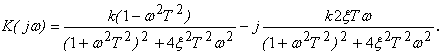
Амплитудно-частотные характеристики (АЧХ) для различных значений x имеет вид (рис. 22б) и определяется соотношением
![]()
Фазовая частотная характеристика (ФЧХ) имеет вид (рис. 22в) и определяется соотношением
![]()
Частотные характеристики колебательного звена имеют вид
а) б) в)
Рис. 22
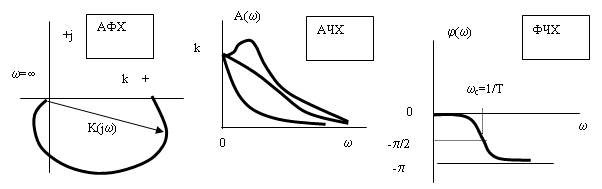
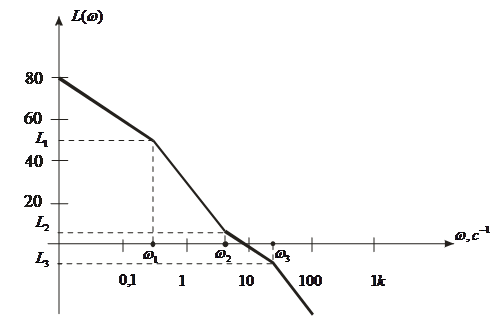
Логарифмические частотные характеристики звена (рис. 23) определяются по формуле:
![]()
При k = 1
![]()
Рис. 23
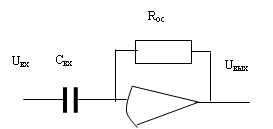
Примеры звена. Колебательное звено может быть реализовано на операционных усилителях (рис. 24).
Рис. 24
Колебательное звено на RLC-цепи (рис. 25).
|
| |||||
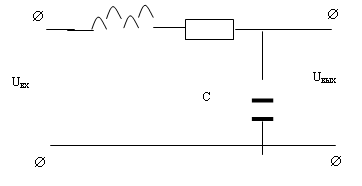 | ||||||
Рис. 25
В приведенной схеме:
С – накапливает энергию электрического поля;
L – накапливает энергию электромагнитного поля;
R – на сопротивлении происходит потеря энергии.
Запишем передаточную функцию цепи:
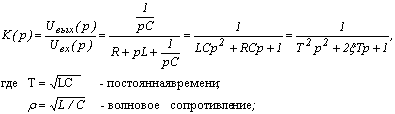
![]() – затухание (демпфирование).
– затухание (демпфирование).
4. Механические демпферы (рис. 26).
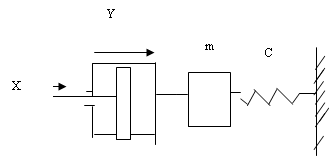
Рис. 26
Форсирующее звено. Форсирующим называют звено, которое описывается уравнением:
![]() (13)
(13)
или передаточной функцией
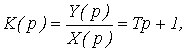 (14)
(14)
где k – коэффициент передачи звена.
При этом переходная функция звена и его функция веса соответственно определяются соотношениями:
![]()
![]()
Частотные характеристики звена (рис. 27а-в) определяются соотношениями:
![]()
1
 | ||
а) б) в)
Рис. 27
Логарифмические частотные характеристики звена (рис. 28) определяются по формуле:
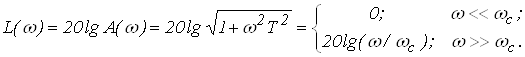

Рис. 28
Форсирующее звено 2-го порядка. Передаточная функция форсирующего звена 2-го порядка имеет вид:
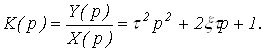 (15)
(15)
Логарифмические частотные характеристики звена имеют вид:
Запаздывающее звено. Дифференциальное уравнение и передаточная функция запаздывающего звена имеют вид:
![]() (16)
(16)
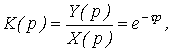 (17)
(17)
где t – время запаздывания.
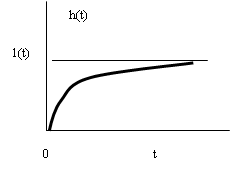
В соответствии с теоремой запаздывания ![]() . При этом переходная функция звена и его функция веса (рис. 30а, б) соответственно определяются соотношениями:
. При этом переходная функция звена и его функция веса (рис. 30а, б) соответственно определяются соотношениями:
![]()
![]()
 | |||
 | |||
Рис. 30
Частотные характеристики звена (рис. 31а-в) определяются соотношениями:
![]()
 | |||
а) б) в)
Рис. 31
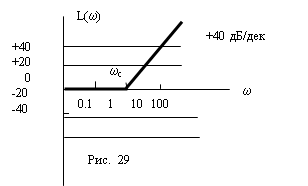
Устойчивые и неустойчивые звенья. В устойчивых звеньях переходный процесс является сходящимся, а в неустойчивых он расходится. Устойчивые звенья называются минимально – фазовыми. Эти звенья не содержат нулей и полюсов в правой полуплоскости корней. Неустойчивые звенья называются не минимально – фазовыми. Т. е. изменению амплитуды на ±20 дБ/дек соответствует изменение фазы на ±p/2, а ±40 дБ/дек – на ±p.
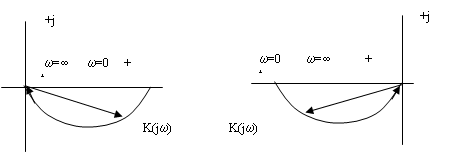
Пример 1. Построить частотные характеристики для звеньев

Для заданных передаточных функций звеньев, характеристики имеют вид (рис. 32):
 | |||||||
 | |||||||
 | |||||||
 | |||||||
Рис. 32
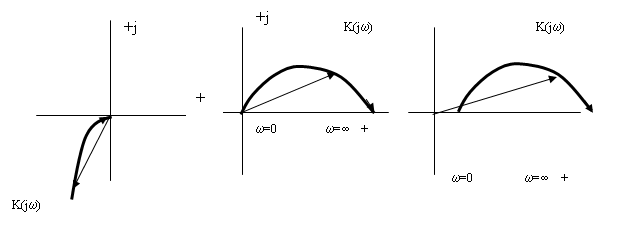
Идеальные и реальные звенья. Идеальные звенья физически не реализуемы, реальные звенья содержат инерционности.
 реальное интегрирующее звено;
реальное интегрирующее звено;
 реальное дифференцирующее звено;
реальное дифференцирующее звено;
 реальное форсирующее звено.
реальное форсирующее звено.
АФХ этих звеньев имеют вид (рис. 33а-в):
а) б) в)
| ||||
| ||||
Рассмотрим характеристики соединений звеньев и порядок построения логарифмических частотных характеристик соединений звеньев.
1. Определяем, из каких элементарных звеньев состоит соединение.
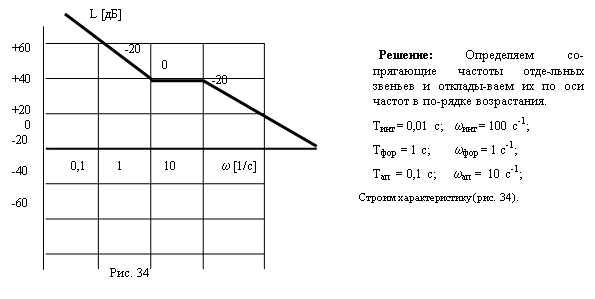
2. Определяем сопрягающие частоты отдельных звеньев и откладываем их по оси частот в порядке возрастания.
3. Определяем наклон низкочастотной асимптоты, используя формулу [(l-m) 20] дБ/дек (где l – количество дифференцирующих, а m- интегрирующих звеньев) и проводим ее через соответствующую сопряженную частоту.
4. Последовательно сопрягая звенья, строим характеристику соединения.
Пример 2. Построить логарифмическую частотную характеристику соединения:
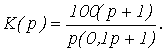
Пример 3. Построить логарифмическую частотную характеристику соединения

![]()
![]()

![]()
![]()
|

 | |||||
 | |||||
| |||||
Пример 4. Построить АФХ соединения звеньев, передаточная функция которого имеет вид
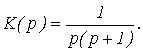
Решение: Выполнив подстановку p = jw и умножив на комплексно сопряженное выражение, получим

Строим характеристику рис. 36.
|
![]() +j
+j
|
+

Рис. 36
Литература
1. Автоматизированное проектирование систем автоматического управления. / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1990. -332 с.
2. Бойко Н.П., Стеклов В.К. Системы автоматического управления на базе микро-ЭВМ. – К.: Тэхника, 1989. –182 с.
3. В.А. Бесекерский, Е.П. Попов «Теория систем автоматического управления». Профессия, 2003 г. – 752 с.
4. Гринченко А.Г. Теория автоматического управления: Учебн. пособие. – Харьков: ХГПУ, 2000. –272 с.
5. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.
Похожие работы
... прямую на ось , то это и будет сопрягающая частота. Постоянную времени можно определить, зная сопрягающую частоту : . c. Исследование частотных характеристик апериодического звена 2-го порядка Для исследования частотных характеристик апериодического звена 2-го порядка в прикладном пакете ProteusISIS составляем структурную схему, представленную на рисунке 16, при неизменной первой постоянной ...
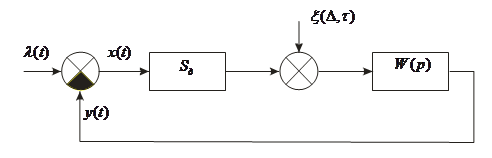
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
... 61508;Х=Хвх+-Хо.с. и решив их совместно получим ур-е W=Wпр/(1+-Wпр*Wо.с.) Структурные методы широко используются в инженерной практике для характеристики процессов в элементах и системах автоматики Структурные схемы элементов автоматических систем формируются на основе совокупности ур-ий, которые связывают характеристики процесса с параметрами и начальными условиями этого процесса в сочетании с ...
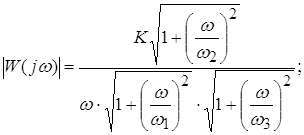
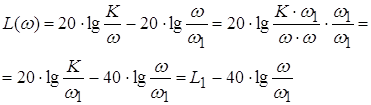
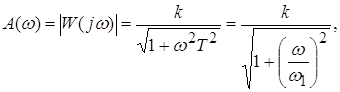

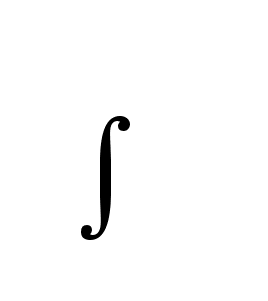
0 комментариев