Навигация
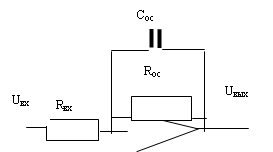
Апериодическое звено может быть реализовано на операционных усилителях (рис. 9)
1. Апериодическое звено может быть реализовано на операционных усилителях (рис. 9).
 | |||
 | |||
![]() Æ Æ
Æ Æ
Рис. 9
2. Звенья на RLC-цепях (рис. 10).
|
![]()
![]()
![]()
![]()
![]()
|
|
|
|
| |||||||||
| |||||||||
| |||||||||
Æ Æ Æ Æ
Рис. 10
4. Механические демпферы (рис. 11).
| |||
 | |||
Рис. 11
Интегрирующее звено. Интегрирующим звеном называют звено, которое описывается уравнением:
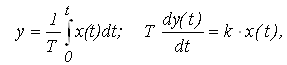 (6)
(6)
или передаточной функцией:
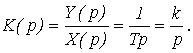 (7)
(7)
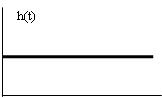
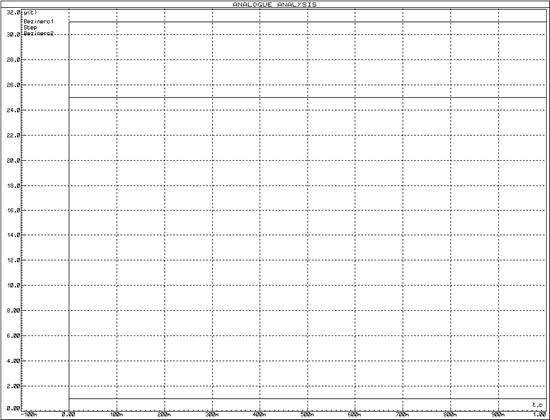
При этом переходная функция интегрирующего звена (рис. 12а) и его функция веса (рис. 12б) соответственно имеют вид:


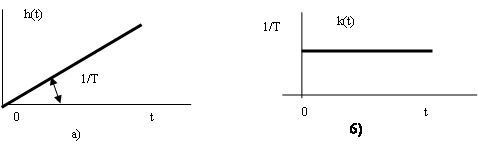
Рис. 12
Частотные характеристики интегрирующего звена (рис. 13) определяются соотношениями:
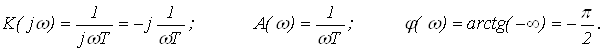
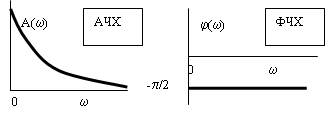 | ||||||
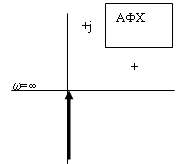 | ||||||
 | ||||||
 | ||||||
Рис. 13
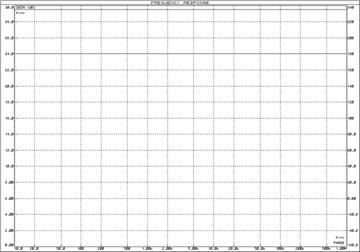
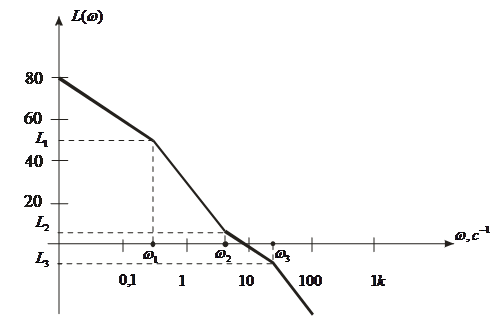
Логарифмические частотные характеристики интегрирующего звена (рис. 14) определяются по формуле:
![]()
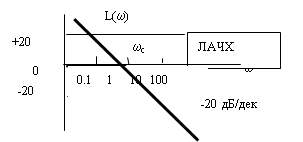
Рис. 14
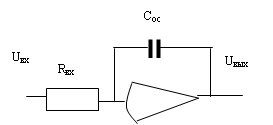
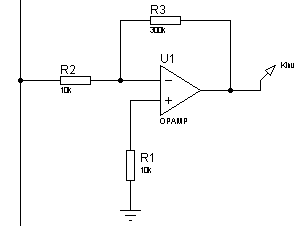
Пример звена. Интегрирующее звено может быть реализовано на операционных усилителях (рис. 15).
 | |||
|
Æ Æ
Рис. 15
Дифференцирующее звено. Дифференцирующим называют звено, которое описывается уравнением:
![]() (8)
(8)
или передаточной функцией:
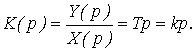 (9)
(9)
При этом переходная функция звена (рис. 16а) и его функция веса (рис. 16б) соответственно имеют вид:
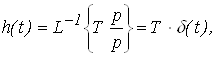
![]()
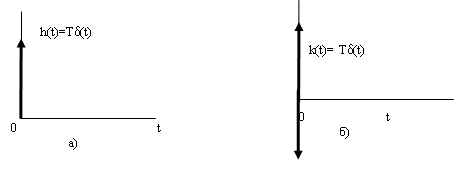
Рис. 16
Частотные характеристики звена (рис. 17а-в) определяются соотношениями:
![]()
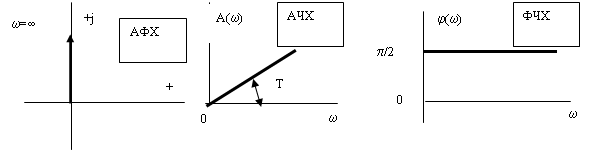 | ||||
 | ||||
а) б) б)
Рис. 17
Идеальное дифференцирующее звено является физически не реализуемым. В реальных звеньях такой вид характеристики могут иметь только в ограниченном диапазоне частот.
Логарифмические частотные характеристики звена (рис. 18) определяются по формуле:
![]()

Рис. 18
Примеры звена:
Похожие работы
... прямую на ось , то это и будет сопрягающая частота. Постоянную времени можно определить, зная сопрягающую частоту : . c. Исследование частотных характеристик апериодического звена 2-го порядка Для исследования частотных характеристик апериодического звена 2-го порядка в прикладном пакете ProteusISIS составляем структурную схему, представленную на рисунке 16, при неизменной первой постоянной ...
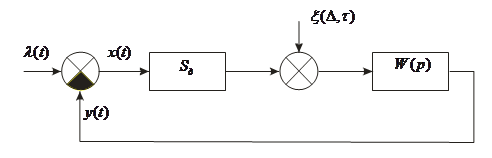
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
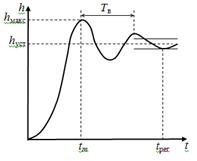
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
... 61508;Х=Хвх+-Хо.с. и решив их совместно получим ур-е W=Wпр/(1+-Wпр*Wо.с.) Структурные методы широко используются в инженерной практике для характеристики процессов в элементах и системах автоматики Структурные схемы элементов автоматических систем формируются на основе совокупности ур-ий, которые связывают характеристики процесса с параметрами и начальными условиями этого процесса в сочетании с ...
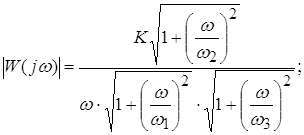

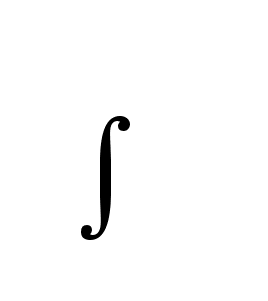
0 комментариев