Визначення періоду дискретизації імпульсного елемента

4.1 Визначення періоду дискретизації імпульсного елемента.

 

В якості формоутворювача сигналу приймемо екстраполятор нульового порядку.

ωз = 43,2 с-1 – максимальна частота в спектрі вхідного сигналу.

За теоремою Котельникова для нормальної роботи системи необхідно, щоб виконувалася умова Tk =  - період дискретизації, ωк ≥ 2ωз – частота дискретизації. Оберемо ωк ≥ 2·43,2 = 86,4 с-1, тоді

Tk ≤ (с)

Виберемо період дискретизації Tk = 0,01с, ωк = 90 с-1.

4.2 Визначення передаточної функції розімкнутої та замкнутої ДСАК відносно вхідної дії

 

w(z) = .

Спочатку розкладемо функцію на простіші дроби:

.

Виконаємо z-перетворення Лапласа отриманої функції:

. Отже,

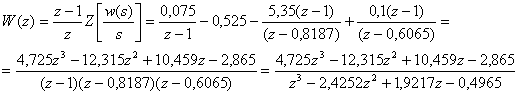
Передатна функція замкненої ДСАК:

.

4.3 Визначення стійкості отриманої системи по критерію Гурвіца

Знаючи перехідну функцію, знайдемо характеристичне рівняння системи: D(s)=.

Виконаємо білінійне перетворення

.

Отримаємо наступне характеристичне рівняння:

На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:

D = .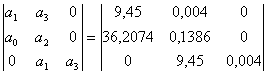

За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а0>0 всі визначники Гурвіца були додатними.

а0= 36,2074>0,

Умова стійкості системи виконуються, отже за критерієм Гурвіца САК стійка.

4.4 Побудова логарифмічної псевдочастотної характеристики ДСАК та визначення запасів стійкості

Для побудови логарифмічної псевдочастотної характеристики використаємо передаточну функцію розімкненої системи після корекції та виконання z- перетворення:

Виконаємо 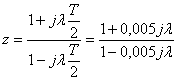, де l - абсолютна псевдочастота, с-1.

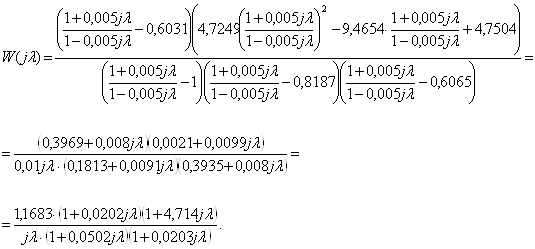
Знайдемо нульову контрольну точку: L0 = 20lgk = 20lg1,1683 = 1,351 дБ.

Визначимо спряжені частоти: λ1 =  = 19,9с-1, λ2 =  = 49,3с-1,

λ3 =  = 49,5с-1, λ4 =  = 0,212с-1.

Враховуючи, що до складу системи входить пропорційна, інтегруюча, дві аперіодичні ланки першого порядку та дві форсуючі ланки, отримуємо ЛАХ і ЛФХ для даної САК (рис. 17).

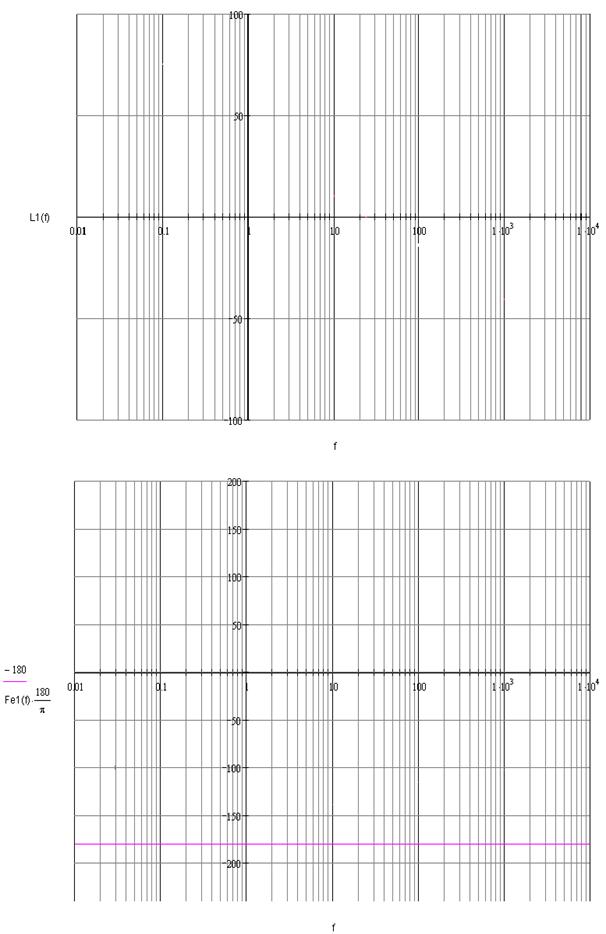
Рис. 17. Логарифмічні частотні характеристики системи

Знайдемо запаси стійкості системи за ЛАХ та ЛФХ:

· по амплітуді запас стійкості h=µ (DL), тому що ЛФХ не перетинає межу -p.

· по фазі: Δφ = π-Arg(w(j*ωз)), де ωз – частота зрізу, коли L(ωз) = 1, тобто

ωз = 24. Тоді Δφ = arg(w(j*24) = -34°.

 

4.5 Розрахунок та побудова графіку перехідної характеристики ДСАК

 

Для побудови перехідної характеристики ДСАК використаємо перехідну характеристику замкненої системи отриману раніше.

Розрахуємо перехідну характеристику ДЦСАК Y(z) = Ф(z)*G(z), де G(z) =  - зображення вхідного одиничного сигналу. Тобто

.

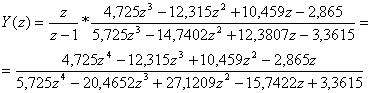Побудуємо графік перехідного процесу, попередньо розклавши перехідні характеристики в ряд Лорана:

_

 

 _

 

 _

 

 _

 

 _

 

Тобто С0=0,8253, C1 = 0,7991, C2 = 0,7739, C3 = 0,7498, C4 = 0,7269, C5 = 0,7053. За цими даними побудуємо графік - гістограму перехідного процесу (рис. 18).

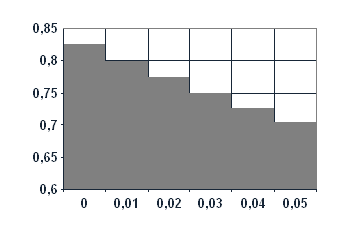
Рис. 18. Перехідна характеристика досліджуваної ДСАК

Провівши розрахунки та побудову за допомогою Math Lab отримали такі результати:

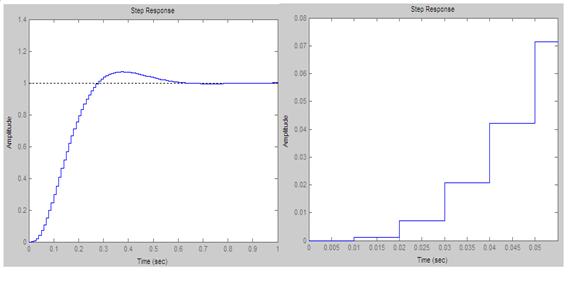
Отримані перехідні характеристики не співпадають, що означає неточність розрахунків, а також специфіка розрахунку передаточних відношень в Math Lab.