Навигация
Содержание
1. Способы представления и параметры
2. Элементы R,L,C в цепи синусоидального тока
3. Алгебра комплексных чисел
4. Символический метод
5. Законы цепей в символической форме
Список литературы
1. Способы представления и параметры
Переменный ток (напряжение) – это ток (напряжение), изменяющийся во времени либо по величине, либо по направлению, либо и по величине и по направлению. Частным случаем переменного тока является периодический ток.
Минимальный промежуток времени, по истечении которого повторяются мгновенные значения в том же порядке, называется периодом T [с] функции.
Синусоидальные токи и напряжения – это частный случай периодических токов и напряжений:
![]()
Величину обратную периоду называют частотой: ![]() [Гц].
[Гц].
Периодические токи и напряжения характеризуются:
- амплитудным значением (Im, Um) – максимальным значением за период;
- средним значением (I0 ,, IСР , U0,, UСР)
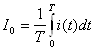 ;
;
- средневыпрямленным значением (Iср. в., Uср. в.)
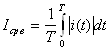 ;
;
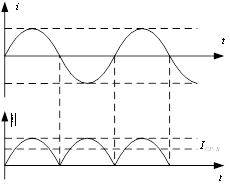
- действующим значением (I, U, Е, J).
Действующим значением периодического тока ![]() называется такая величина постоянного тока, которая за период оказывает такое же тепловое действие, что и периодический ток.
называется такая величина постоянного тока, которая за период оказывает такое же тепловое действие, что и периодический ток.
Пусть
![]()
тогда мгновенная мощность переменного тока:
![]() .
.
Энергия, выделяющаяся за период в сопротивлении
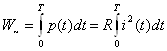 .
.
Пусть по тому же сопротивлению R протекает постоянный ток, тогда мгновенная мощность постоянна: ![]()
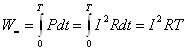 .
.
Приравнивая энергии ![]() и
и ![]() , получим величину постоянного тока, оказывающего такое же тепловое действие, что и периодический ток, т.е. действующее значение периодического тока:
, получим величину постоянного тока, оказывающего такое же тепловое действие, что и периодический ток, т.е. действующее значение периодического тока:
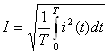 .
.
Аналогично записывают формулу для действующего значения напряжения.
Активная мощность Р - это среднее значение мгновенной мощности за период:
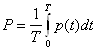 .
.
Наиболее распространенным периодическим током является синусоидальный ток. Это связано с тем, что периодические сигналы , встречающиеся в электротехнике, можно представить в виде суммы синусоидальных функций кратных частот (ряд Фурье) и синусоидальный режим является наиболее экономичным режимом в цепях (минимальные потери).
В стандартной форме синусоидальные токи и напряжения записывают следующим образом:
![]() и
и ![]()
- ![]() и
и ![]() - амплитудные значения,
- амплитудные значения,
- ![]() - называется фазой и показывает состояние, в котором находится изменяющаяся величина.
- называется фазой и показывает состояние, в котором находится изменяющаяся величина.
- ![]() - угловая частота,
- угловая частота,
- ![]() - начальная фаза, т.е. фаза в момент начала отсчета времени. На графике начальную фазу определяют от момента перехода синусоиды с отрицательных значений к положительным до начала координат.
- начальная фаза, т.е. фаза в момент начала отсчета времени. На графике начальную фазу определяют от момента перехода синусоиды с отрицательных значений к положительным до начала координат.
![]()
Два колебания одинаковой частоты совпадают по фазе, если у них одинаковые начальные фазы; сдвинуты по фазе, если у них разные начальные фазы. Синусоида с большей начальной фазой опережает синусоиду с меньшей начальной фазой. Если сдвиг фаз равен ![]() говорят, что синусоиды в противофазе. Если сдвиг фаз
говорят, что синусоиды в противофазе. Если сдвиг фаз ![]() , то синусоиды в квадратуре.
, то синусоиды в квадратуре.
Для синусоидальных колебаний имеем:

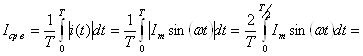
![]()
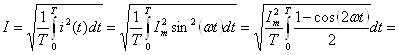
![]()
Интеграл от второго слагаемого =0 (см. вывод среднего значения).
В цепях синусоидального тока и напряжения мощность в каждый момент времени различна. Поэтому из равенства теплового действия выводят понятие активной мощности Р.
Похожие работы
... можно строить схемы замещения реальных элементов цепи. 3. Топологические элементы схем Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи. Основные понятия: 1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток. 2) Узел – место соединения трех и более ветвей ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... соотношений и решает задачу вычисления реакции линейной электрической цепи на заданное непрерывное воздействие по известной переходной характеристики цепи . Эти соотношения называют интегралами Дюамеля. 3. Импульсные характеристики электрических цепей Импульсной характеристикой цепи называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных ...
... Токи и находим по правилу деления тока : ; Напряжения на резисторах по известным токам в них вычисляются по закону Ома. Расчет резистивных электрических цепей методом токов ветвей Расчет сложных резистивных цепей, т. е. цепей, не сводящихся к последовательному или параллельному соединению элементов, основывается на использовании законов Кирхгофа. Если цепь имеет элементов, то ...







0 комментариев