Навигация
Элементы R,L,C в цепи синусоидального тока
2. Элементы R,L,C в цепи синусоидального тока
Пусть через каждый элемент протекает синусоидальный ток ![]() .
.
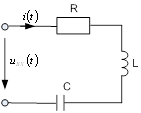
Тогда, согласно компонентным уравнениям и с учетом синусоидальности тока получаем:
![]() ;
;
![]() ;
;
![]()
Напряжения на элементах в цепи синусоидального тока так же синусоидальны и имеют ту же частоту, но другие амплитуды и начальные фазы. Учитывая стандартную запись напряжения ![]() , получаем
, получаем
| R | L | C |
|
|
|
|
|
|
|
|
Напряжение на сопротивлении совпадает с током по фазе, напряжение на емкости отстает от тока на 900, напряжение на индуктивности опережает ток на 900.
Определим мгновенную и активную мощности на каждом элементе:
![]()
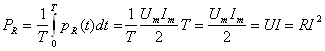 ;
;
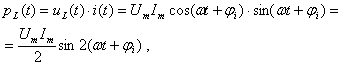
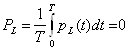 ;
;
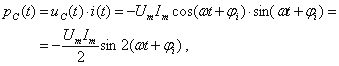
 .
.
для R

для L
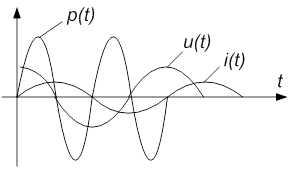
для C

Таким образом, мгновенная мощность во всех элементах изменяется с двойной частотой тока. Однако мгновенная мощность в сопротивлении R содержит еще постоянную составляющую, поэтому активная мощность получается больше нуля. Индуктивность и емкость активной мощности не потребляют: половину периода мощность поступает от внешней цепи, а во вторую половину периода эти элементы отдают мощность во внешнюю цепь. В те моменты времени, когда индуктивность потребляет активную мощность, емкость генерирует её и наоборот.
Так как сопротивление R потребляет активную мощность, то его называют активным сопротивлением. Индуктивность и емкость активной мощности не потребляют, поэтому их называют реактивными сопротивлениями и обозначают соответственно ![]() [Oм] и
[Oм] и ![]() [Oм].
[Oм].

Для расчета режима в цепи синусоидального тока можно записать систему уравнений по законам Кирхгофа, используя полученные соотношения между напряжением и током на элементах. Это будет система тригонометрических уравнений. Уравнения будут содержать синусоиды различной амплитуды и начальной фазы и необходимо проводить много тригонометрических преобразований, что не всегда удобно. Поэтому разработан специальный метод анализа режимов цепей синусоидального тока – метод комплексных величин или символический метод.
Похожие работы
... можно строить схемы замещения реальных элементов цепи. 3. Топологические элементы схем Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи. Основные понятия: 1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток. 2) Узел – место соединения трех и более ветвей ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... соотношений и решает задачу вычисления реакции линейной электрической цепи на заданное непрерывное воздействие по известной переходной характеристики цепи . Эти соотношения называют интегралами Дюамеля. 3. Импульсные характеристики электрических цепей Импульсной характеристикой цепи называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных ...
... Токи и находим по правилу деления тока : ; Напряжения на резисторах по известным токам в них вычисляются по закону Ома. Расчет резистивных электрических цепей методом токов ветвей Расчет сложных резистивных цепей, т. е. цепей, не сводящихся к последовательному или параллельному соединению элементов, основывается на использовании законов Кирхгофа. Если цепь имеет элементов, то ...







0 комментариев