Розв’язок рівняння для потенціалу для електростатичного зонду в гетерогенному плазмовому середовищі

3. Розв’язок рівняння для потенціалу для електростатичного зонду в гетерогенному плазмовому середовищі.

Запилена плазма є невпорядкованим середовищем, у якому в системі координат зонду розподіли концентрацій заряджених частинок (електронів, іонів, конденсованих частинок) покладаємо підпорядкованими максвел-больцманівській статистиці. Треба зауважити, що у випадку нерівноважних процесів та дії джерел термостату, питання про розподіл зарядів в газовій підсистемі запиленій плазми потребує окремого дослідження. В нерівноважній запиленій плазмі, яка характеризується стаціонарним полем термодинамічних параметрів в об’ємі, виходячи з принципу локальної термодинамічної рівноваги Кубо [13], формули рівноважної термодинаміки необхідно використовувати для областей локальної термодинамічної рівноваги разом з подальшим осередненням (з врахуванням градієнтів) на макрооб’єми.

Потенціал зонда та концентрація електронів у приповерхневому шарі його максвел-больцманівської атмосфери пов’язані співвідношенням

(3.1)

 – локальна концентрація електронів в областях де самоузгоджений потенціал обертається до нуля (в дебаєвських моделях екранування в запиленій плазмі співпадає з середньооб’ємною); ”зовнішній” потенціал поверхні зонда відрахований від рівня вакууму (рівня потенціальної енергії електрона, що покоїться у вакуумі при відсутності зовнішніх полів). В моделі необмеженої слабкоіонізованої запиленої плазми, утвореної електронами, іонами, ідентичними конденсованими частинками та буферним газом [14], рівняння Пуасона-Больцмана для розподілу самоузгодженого електростатичного потенціалу в зовнішній відносно власного об’єму зонда області має дебаєвський розв’язок

 , (3.2)

де: нормований на енергію Фермі речовини зонда потенціал;

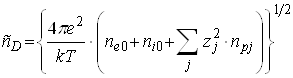– (3.3)

інвертована дебаєвська довжина зарядів плазми,  відповідно середньооб’ємні зліченні концентрації електронів, іонів та макрочастинок сорту “j”; осереднене зарядове число “j - ї” конденсованої частинки:

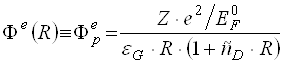– (3.4)

значення потенціалу поверхні зонду, отримане із “зовнішньої задачі” (ze - заряд зонду,  діелектрична проникність буферного газу). В умовах статистичної рівноваги заряд зонду та його потенціал досягають певних сталих величин, які визначаються тільки параметрами плазми та характеристиками зонду і є незалежними від предісторії їх встановлення. Неперервність самоузгодженого електростатичного потенціалу та нормальної складової електростатичної індукції на поверхні зонда є фізичними умовами, що в кінцевому підсумку дають змогу записати функціональні співвідношення між параметрами запиленої плазми та рівноважними значеннями заряду і потенціалу зонда. Оскільки електрони поверхневого (контактного) шару зонду знаходяться в стані динамічної рівноваги з електронним компонентом запиленої плазми, то, згідно з відомим положенням статистичної теорії [15], локальний електрохімічний потенціал електронної підсистеми повинен бути однорідним впродовж запиленої плазми і мати певне усталене значення F. Концентрація електронів на нескінченості, де їх потенціальна енергія покладається нульовою, буде

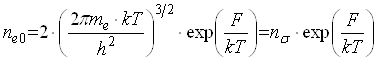(3.5)

Поблизу поверхні зонда у відповідності з больцманівським розподілом (3.1)

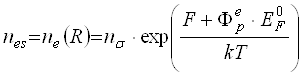(3.6)

Поверхнева концентрація електронів газової фази (3.6) утворює потік електронів прилипання, який врівноважується електронами емісії, що інжектуються поверхнею зонду у газову фазу. Динамічна рівновага цих потоків реалізується для певного значення заряду зонда Z, і є умовою його зарядової стійкості.

Розв’язок задачі Коши (2.2 – 2.4) з використанням лінійної апроксимації для правої частини рівняння Пуасона-Фермі (2.2) за “внутрішнім потенціалом”  доцільно проводити в термінах допоміжних змінних

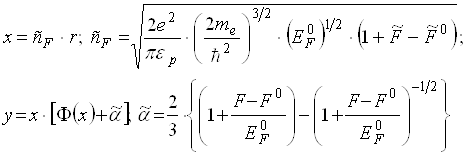(3.7)

В (3.7) і далі позначкою “~” відмічаємо нормування “енергетичних” величин на . У змінних (3.7) задача Коши для розподілу самоузгодженого потенціалу в об’ємі зонда має вид

(3.8)

Загальний розв’язок (3.8) буде

 (3.9)

Таким чином, повертаючись до вихідних змінних , запишемо

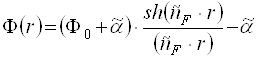(3.10)

Функція (3.10) описує розподіл самоузгодженого електростатичного потенціалу всередині зонду. Із умови спряження для нормальної похідної потенціалу Ф на поверхні сферичного зонду отримаємо

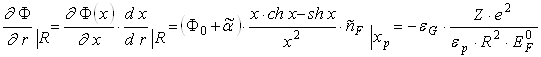(3.11)

Формула (3.11) встановлює зв’язок між потенціалом в центрі зонду та його зарядовим числом Z. З умови неперервності електростатичного потенціалу на поверхні зондуючого тіла (умови спряження “зовнішнього” – (3.3), та “внутрішнього” – (3.10), потенціалів після підстановки  з (3.11) в (3.10) ) кінцево отримуємо трансцендентне рівняння для потенціалу поверхні зонду як функції заряду та визначальних параметрів запиленої плазми

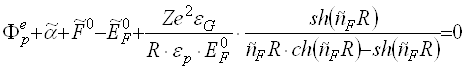(3.12)

Для певного значення електрохімічного потенціалу (рівня Фермі) електронів плазми F рівняння (3.12) встановлює однозначний зв’язок між потенціалом  та зарядом , що їх набуває зонд в результаті взаємодії з плазмовим середовищем. Незалежні експериментальні виміри цих величин дозволили б, шляхом вирішення оберненої задачі (3.12) для рівня Фермі запиленої плазми, за допомогою рівняння (3.5) отримати з даних експерименту невідоме значення електронної концентрації в об’ємі запиленої плазми.

У розділі 4 обговоримо можливу принципову схему та деталі експерименту з визначення рівня іонізації запиленої плазми з використанням двох пасивних зондів.