Комп’ютерний експеримент

4. Комп’ютерний експеримент

Параметри ізольованого металевого зонду в запиленій плазмі можна експериментально визначити, грунтуючись на класичній методиці зондових вимірювань [3] у якій пасивний зонд з’єднується з землею через дуже великий опір R_Z, такий, щоб струм витоку практично не змінював рівноважні параметри зонду, і в той же час був достатнім для вимірів падіння напруги на R_Z (мал. 2) .

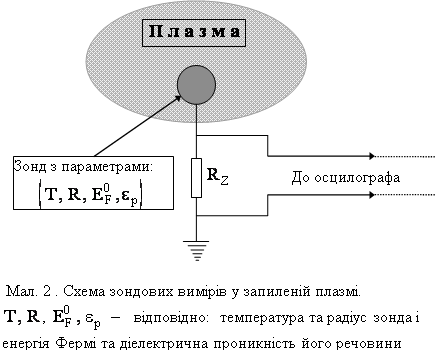
Різниця потенціалів між поверхнею зонду та землею за вирахуванням термоелектричних падінь напруги, що виникають у з’єднувальних провідниках, дає так званий “плаваючий потенціал” зонду, що контактує з плазмою [9]. В умовах слабкоіонізованої дебаєвської запиленої плазми осереднене за часом значення потенціалу зонда з одного боку обчислюється за формулою (3.4), з іншого - може бути визначеним з рівняння (3.12). Оскільки в дебаєвському наближенні потенціал (3.4) є функцією від заряда та радіуса зонда, а також енергії Фермі та діелектричної проникності його речовини, то помістивши в плазму два незалежних зонди, виготовлених з різних металів, але такі, що мають однаковий геометричний розмір, базпосередньо з формул (3.4) та (3.12) отримаємо

 (3.13)

Для металів ~ см^-1 , і останніми доданками в чисельнику та знаменнику даної формули можна знехтувати. В результаті остаточно, в рамках пропонуємої двозондової методики, отримуємо рівняння для визначення рівня Фермі електронів запиленої плазми

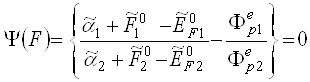(3.14)

Електрохімічний потенціал F, що входить як невідоме в трансцендентне рівняння (3.14), згідно з формулою (3.5) є безпосередньо пов’язаним з рівнем іонізації плазми . Отже, отримавши потенціали незалежних зондів  в експерименті, шляхом розв’язку рівняння (3.14) отримуємо невідомий рівень Фермі електронів F у запиленій плазмі .

В рамках викладеного методу, на основі програми розв’язку трансцендентних рівнянь PNFFM [9], було проведено комп’ютерну симуляцію щодо визначення іонізації запиленої плазми в широкому діапазоні її термодинамічних параметрів, що є характерними для впроваджень. На мал. 3а та 3б наведено графіки залежностей безрозмірного (нормованого на енергію Фермі речовини зонду “1”) F, як функції відношення плаваючих потенціалів, отримані на основі даних обчислювального експерименту. Зазначимо, що фізично, навпаки: відношення потенціалів зондів є функцією F, але в експерименті ми вирішуємо обернену задачу, тому аналізуємо обернені функції .

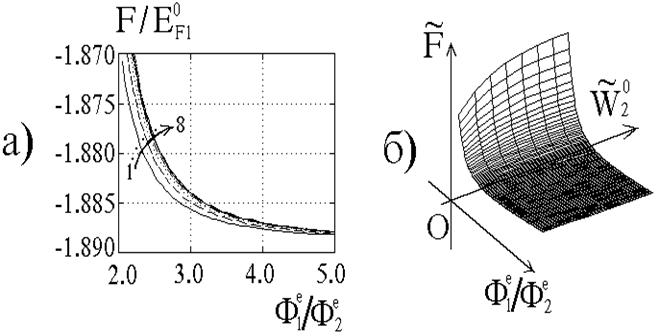
Мал.3. Значення безрозмірного рівня Фермі електронів запиленої плазми, нормованого на енергію Фермі базового зонду . Графіки відображують варіант обчислювального експерименту для підпростору визначальних параметрів ЗП: (,,4.5, 4.6, 4.0 еВ: [4.2, 5.8] еВ; [ 2, 5 ].

Радіуси сферичних зондів покладались однаковими, причому такими, що  (для зондів з  мм відносна похибка, яку вносять відкинуті в (3.13) доданки, вже не перевищує 10^-5). Роботи виходу металів, що з них виготовлено зонди, та енергії Фермі електронів провідності обирались з інтервалу еВ, який охоплює практично всі відомі значення цих величин для твердих матеріалів [16] . Якісно графіки електрохімічного потенціалу запиленої плазми, як це видно з мал.3, є подібними, і із збільшенням різниці робіт виходу речовини зондів мають тенденцію до зростання (див. зміщення кривих 1¸8 у напрямку стрілки - мал.3а, та трансформації просторового графіку впродовж осі на мал.3б ).

Висновок

Запропонований зондовий метод є одним з актуальних сучасних методів вимірювання електрофізичних характеристик гетерогеної плазмової середи, який засновувався на апроксимації Томаса-Фермі для дисперсійного рівняння електронів провідності зонду. Користуючись комп’ютерною симуляцією експерименту було визначено залежності потенціалу усамітненого зонду від визначальних термодинамічних параметрів плазмового середовища.

Таким чином, для більш точних вимірів F в двозондовій методиці необхідно використовувати зонди з металів, які якомога більше відрізняються за роботою виходу. Оскільки в термічній гетерогенній плазмі електростатичний потенціал пасивного зонду буде ~ kT << , то даний метод вимірювань рівня Фермі є безпосередньо застосовним для багатьох видів запилених плазм у впровадженнях.

Література

1.  Цытович В. Н. Плазменно-пылевые кристаллы, капли и облака// Успехи физических наук. - 1997.-Т. 167, N 1, С. 57 - 99 .

2.  Маренков В.І. Вплив електронних та діелектричних властивостей металу на іонізацію гетерогенної плазми, утвореної буферним газом та ансамблем емітуючих металевих макрочастинок// Вісник Одеського державного університету.- Одеса, 2000, Т.5, Вип.3, С. 202-208.

3.  Чан П. и др. Электрические зонды в неподвижной и движущейся плазме: (теория и применения/ П. Чан, Л Тэлбот, К. Турян . - М.: Мир, 1978. - 201 с.

4.  Павлов Т. А. Процессы переноса в плазме с сильным кулоновским взаимодействием. - М.: Энергоатомиздат, 1995. - 192 с.

5.  Касаков А. И. Основные понятия физики плазмы// Методические указания. – Грозный, 1983.- С. 3-14.

6.  Козлов В. И. Электрический зонд в плазме// М.: Наука, 1978.- 235 c.

7.  Прохоров А. М. Физическая Энциклопедия// М.: Большая Российская Энциклопедии, 1992.-Т.3, С.350 - 355

8.  Лохте-Хольтгревен В. Методы исследования плазмы// М.: Мир, 1971. С. 459 – 502.

9.  Маренков В.И.,Чесноков М.Н. Физические модели плазмы с конденсированной дисперсной фазой. - Киев: УМК ВО, 1989, 188 с.

10.  Смирнов Б.М. Кластерная плазма. - УФН, 2000, Т. 170, №5, С. 495-534.

11.  Кайзер Дж. Статистическая термодинамика неравновесніх процессов. - М.: Мир, 1990. - 608 с.

12.  Marenkov V.I., Zakharchenko V.L. Physical modelling of ionization state of dense high-temperature plasmasol on the basis of Tomas-Fermi approximation for macroparticles electron component. - MECO 24, Middle European Cooperation in Statistical Physics, March 8th-10th, 1999.-Lutherstadt-Wittenberg,Germany.-1999.-P.43 .

13.  Кубо Р. Статистическая механика. - М.: Мир, 1967. - 452 с.

14.  Маренков В. Электрофизические характеристики плазмы с макрочастицами конденсированной дисперсной фазы и атомами щелочных металлов в газовой фазе// Физика аэродисперсных систем. - Вып. 37, 1998. - С. 128 -143 .

15.  Ландау Л.В., Лифшиц Е.М. Статистическая физика. Ч. 1. - М.: Наука, 1978.-583 с.

16.  Фоменко В.С. Эмиссионное свойства материалов : справочник.- 4-е. изд.- перераб. и доп. - Киев : Наукова думка, 1989. - 339 с.