Навигация
Определение основных размеров маховика
23555
знаков
8
таблиц
1
изображение
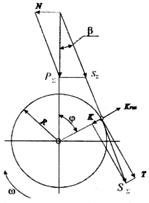
1.3.4. Определение основных размеров маховика Для определения момента инерции маховика методом исключения параметра j строи зависимость приращения кинетической энергии DТ от приведённого момента инерции звеньев (кривую Виттенбауэра).
Определим углы наклона касательных к кривой Виттенбауэра.
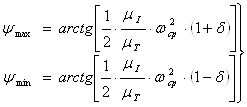(1.23)
где: wср – частота вращения, мин-1.
mI и mТ – масштабные коэффициенты диаграммы энергомас.
d - коэффициент неравномерности движения (задан в ТЗ).
ymax=0030’ ymin=0020’.
После нахождения углов ymax ymin которые отсчитываем от оси Iпр и проводим две касательные к кривой Виттенбауэра, при этом они ни в одной точке не должны пересекать данную кривую. Касательные на оси DТ отсекают отрезок ав, с помощью которого и находим потребную составляющую приведённого момента инерции обеспечивающая движение звена приведения с заданным коэффициентом неравномерности движения.
(1.24)
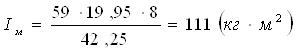
Определяем основные размеры литого маховика по формуле:
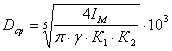(1.25)
где: Dср – средний диаметр обода маховика;
g - плотность материала маховика, кг/м3;
К1,2- принимаем исходя из конструктивных соображений, с учётом приделов(0,1…0,2). К1,2=0,2.
Определим размеры поперечного сечения обода маховика.
а=К1.Dср; а=0,2.854=170(мм);
в=К2.Dср; в=0,2.854=170(мм).
2.Силовое исследование механизма
Задачей силового исследования рычажного механизма является определение реакций в кинематические парах от действия заданных сил. При этом закон движения начальных звеньев является заданным. Результаты силового исследования применяются при определении: сил трения, возникающих в кинематических парах; геометрических параметров звеньев механизма; мощности, потребляемой механизмом для преодоления внешних сил.
При определении реакций в кинематических парах будем использовать принцип Даламбера, согласно которому звено механизма можно рассматривать как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции. Составим уравнения равновесия, которые называют уравнениями кинетостатики.
В результате движении механизма на его звенья действуют силы: движущие, полезных и вредных сопротивлений, тяжести звеньев, инерции звеньев. Из перечисленных сил нам заданны только силы полезных сопротивлений, а остальные подлежат определению.
Bсe силы инерция звена при его движении сведём к главному вектору сил инерции Fи, проложенному к центру масс эвена, и главному моменту Ми сил инерции.
Сила инерции имеет направление, противоположное ускорению центра масс звена. Момент пары сил инерции направлен противоположно угловому ускорению звена. Ускорения центров масс и угловые ускорения звеньев определяются с помощью планов ускорений.
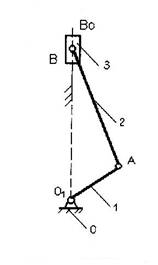
Строим план механизма в масштабе:
ml=0.003(м/мм).
2.1 Построение плана скоростей
Проводим построение плана скоростей по ранее проделанной методике.
Определим скорость точки А. Зная частоту вращения кривошипа О1А и его длину, определим скорость точки А, используя формулу:
(2.1)
(2.2)
где n1 – частота вращения кривошипа.
=6,5(рад/с)
=6,5×0,27=1,76(м/с)
Скорость точки А во всех положениях механизма постоянна, и графически выражается вектором ра.
Определим масштабный коэффициент плана скоростей.
(2.3)
где ра – отрезок на плане скоростей определяющий скорость точки А, мм.
Дальнейшее построение плана скоростей проводим согласно пункта 1.2, раздела: «Динамический анализ и синтез рычажного механизма».
2.2 Построение плана ускорений
Ускорение точек звеньев механизма определяем с помощью плана ускорений. Запишем полное ускорение точки А.
(2.4)
Учитывая тот факт, что кривошип вращается с постоянной угловой скоростью то его угловое ускорение аtАО1 равно 0. То есть ускорение точки А состоит только из нормального ускорения, которое направлено по звену к центру вращения кривошипа.
(2.5)
Определяем масштабный коэффициент плана ускорений.
(2.6)
Для определения ускорения точки В, принадлежащей звену 3, воспользуемся теоремой о сложении ускорений в переносном и относительном движениях , тогда:
(2.7)
где: 
- нормальное ускорение точки В относительно точки А.
- тангенциальное ускорение точки В относительно точки А.
аА – ускорение точки А.
- нормальное ускорение точки В относительно точки О2.
- тангенциальное ускорение точки В относительно точки О2.
аО2 – ускорение точки О2, равное 0 так как точка О2 неподвижна.
Решив геометрически систему уравнений будем иметь ускорение точки В.
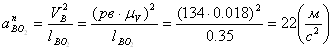
Определим ускорение точки С, для чего составим два векторных уравнения.
(2.8)
где: 
- нормальное ускорение точки С относительно точки В.
- тангенциальное ускорение точки С относительно точки D.
аВ – ускорение точки В.
- кориолисово ускорение, определяется поворотом вектора относительной скорости VССx на 90о в сторону угловой скорости звена 4.
- релятивное (относительное ) ускорение точки Сx, направлено в вдоль звена 5.
Решив геометрически систему уравнений (2.8) будем иметь ускорение точки С.
Похожие работы
... По формуле 106 определяем уравновешивающий момент, Нм: МУР=4670,30,064=298,9 Нм Сравним полученные обоими методами уравновешивающие моменты, %: , (108) 7. Определение коэффициента полезного действия машинного агрегата Машинный агрегат состоит из ДВС, зубчатого редуктора и генератора электрического тока, соединенных последовательно. ДВС состоит из кривошипно-ползунного механизма и ...
... . Расхождение между полученным по графику и рассчитанным в тепловом расчете значениями : ; <. 5 Расчет деталей на прочность 5.1 Поршень Таблица 5.1― Размеры элементов поршневой группы Элементы поршневой группы Расчетные зависимости для карбюраторного двигателя Значения размеров, мм Высота поршня 1,05∙D 104 Расстояние от верхней ...
... 85 231,9 149,4 19,7 10 6018 83,4 248,4 132,4 20,7 11 6600 77,5 269 112,2 20,8 По полученным значениям производим построение внешней скоростной характеристики. 3 Динамический расчет КШМ двигателя 3.1 Расчет сил давления газов Сила давления газов, Н: (3.1) где – атмосферное давление, МПа; , – абсолютное и избыточное давление газов над поршнем в рассматриваемый ...
... двигателя Динамический расчет кривошипно-шатунного механизма выполняется с целью определения суммарных сил и моментов, возникающих от давления газов и от сил инерции. Результаты динамического расчета используются при расчете деталей двигателя на прочность и износ. В течение каждого рабочего цикла силы, действующие в кривошипно-шатунном механизме, непрерывно изменяются по величине и направлению. ...
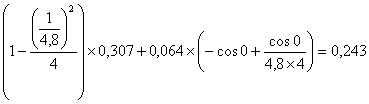
0 комментариев