Навигация
3.1 Задание
3.1.1 Модуль зубчатых колёс планетарного механизма: m1= 3 мм
Числа зубьев колёс простой передачи: Z1=15 , Z2=30;
Модуль зубчатых колёс Z1и Z2: m=6 мм;
Все зубчатые колёса должны быть нулевыми. А это значить, что во избежание подреза ножки зуба для колёс с внешним зацеплением принимают Z>17, для колёс с внутренним зацеплением Z>85.
Подберём числа зубьев Z1,Z2,Z3 для зубчатой передачи с передаточным отношением U=nдв/n1=720/62=11,6.
Задаёмся числом зубьев Z1 из ряда Z1=17,18,19,…. Пусть Z1=20. Число зубьев Z3 найдём из выражения:
![]() (3.1)
(3.1)
где: U1H – передаточное отношение планетарной передачи входного колеса к выходному звену (водилу) при неподвижном опорном колесе.
![]()
![]() (3.2)
(3.2)
где: Uр – передаточное число одной ступени редуктора.
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]()
![]()
Из формулы (1.1) найдём Z3.
![]()
Условие Z3>Zmin=85 выполняется.
Оси центральных колёс и водила должны совпадать между собой, т.е. должно соблюдаться условие соосности, которое имеет вид:
Z1+2Z2=Z3 (3.5)
Из условия соосности находим Z2.
Z2=(Z3-Z1)/2=(96-20)/2=38
Сателлиты должны быть с таким окружным шагом, чтобы между окружностями вершин соседних сателлитов обеспечивался гарантированный зазор- условие соседства:
Sin(1800/k)>(Z2+2)/(Z1+Z2) (3.6)
где: к - число сателитов.
Из условия соседства определяем возможное число сателлитов в механизме.
![]()
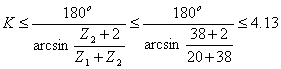
Значит, для этого механизма число сателлитов может быть взято равным 2,3 и 4. Принимаем k=4. Проверяем условие сборки.
Сборка сателлитов должна осуществляться без натягов при равных окружных шагах между ними. Это возможно при выполнении следующего условия:
где: Ц и р целые числа.
![]() (3.7)
(3.7)
Проверку ведём при р=0.
![]()
![]()
Условие сборки выполняется т.к. Ц получилось целое число.
Все условия выполняются, значит окончательно принимаем Z1=20; Z2=38; Z3=96; k=4.
Для построения кинематической схемы механизма определим радиусы делительных окружностей.![]()

![]() (3.8)
(3.8)
 (3.9)
(3.9)
 (3.10)
(3.10)
3.1.2 Расчёт внешнего зацепления пары прямозубых колёс эвольвентных профилей с неподвижными осями, нарезанных стандартной инструментальной рейкой
Окружной шаг по делительной окружности:
Р=p.m (3.11)
где: m – модуль зубчатой передачи.
Р=3.14.6=18,85(мм)
Угловые шаги:
t=2p/Z (3.12)
t1=2×3,14/15=0,42 t2=2×3,14/30=0,21
Радиус делительной окружности:
r=0.5m.Z (3.13)
r1=0.5×6.15=45(мм); r2=0.5×6.30=90(мм)
Радиус основной окружности:
rв=0.5.m.Z.cosa; (3.14)
где: a - угол профиля рейки rв=0.5.m.Z.cosa;, a=200:
rв1=0.5.6.15.cos20 =42,29(мм) rв2=0.5.6.30.cos20 =84,57 (мм)
Определим относительное смещение инструментальной рейки при нарезании
Х1=Х2=0,5
Толщина зуба по делительной окружности:
S=m(p/2+2x.tga); (3.15)
S1=6(3.14/2+2×0,5×tg20)=11,61(мм) S2=6(3,14/2+2×0,5×tg20)=11,61(мм);
Инволюта угла зацепления:
invaw= inva + 2[(x1+x2)/(Z1+Z2)]tga; (3.16)
Invaw= inv20 + 2[(0,5+0,5)/(15+30)]tg20=0,03108;
aw=25017’
Радиус начальной окружности:
rw=0.5m.Z1.cosa/cosaw; (3.17)
rw1=0.5×6.15.cos20/cos25о17’=46,77(мм) rw2=0.5×6.30.cos20/cos25о17’=93,53(мм);
Межосевое расстояние:
aw=0.5m(.Z1+Z2).cosa/cosaw; (3.18)
aw=0.5×6×(.15+30).cos20/cos25о17’=140,30(мм);
Радиус окружности впадин:
rf=0.5m(Z1-2.5+2x); (3.19)
rf1=0.5×6×(15-2.5+2×0.5)=40,5(мм) rf2=0.5×6×(30-2.5+2×0.5)=85,5(мм)
Радиус окружности вершин:
ra1=aw-rf2-0.25m; (3.20)
ra2=aw-rf1-0.25m; (3.21)
ra1=140,30-85,5-0.25×6=53,3(м) ra2=140,30-40,5-0.25×6=98,3(мм);
Похожие работы
... По формуле 106 определяем уравновешивающий момент, Нм: МУР=4670,30,064=298,9 Нм Сравним полученные обоими методами уравновешивающие моменты, %: , (108) 7. Определение коэффициента полезного действия машинного агрегата Машинный агрегат состоит из ДВС, зубчатого редуктора и генератора электрического тока, соединенных последовательно. ДВС состоит из кривошипно-ползунного механизма и ...
... . Расхождение между полученным по графику и рассчитанным в тепловом расчете значениями : ; <. 5 Расчет деталей на прочность 5.1 Поршень Таблица 5.1― Размеры элементов поршневой группы Элементы поршневой группы Расчетные зависимости для карбюраторного двигателя Значения размеров, мм Высота поршня 1,05∙D 104 Расстояние от верхней ...
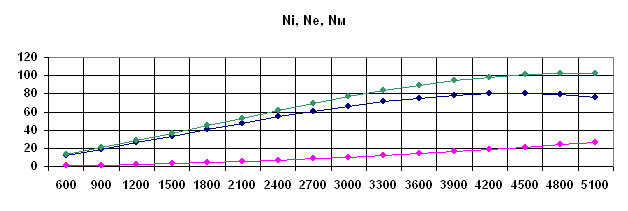
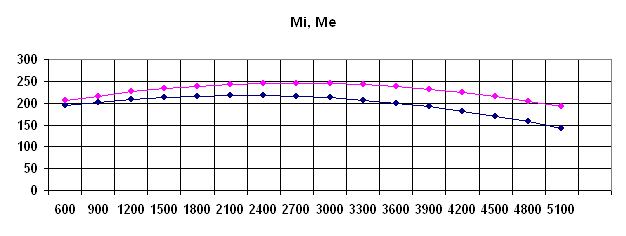
... 85 231,9 149,4 19,7 10 6018 83,4 248,4 132,4 20,7 11 6600 77,5 269 112,2 20,8 По полученным значениям производим построение внешней скоростной характеристики. 3 Динамический расчет КШМ двигателя 3.1 Расчет сил давления газов Сила давления газов, Н: (3.1) где – атмосферное давление, МПа; , – абсолютное и избыточное давление газов над поршнем в рассматриваемый ...
... двигателя Динамический расчет кривошипно-шатунного механизма выполняется с целью определения суммарных сил и моментов, возникающих от давления газов и от сил инерции. Результаты динамического расчета используются при расчете деталей двигателя на прочность и износ. В течение каждого рабочего цикла силы, действующие в кривошипно-шатунном механизме, непрерывно изменяются по величине и направлению. ...


0 комментариев