Навигация
Расчёт амплитуды и частоты периодических режимов графоаналитическим методом гармонического баланса
2. Расчёт амплитуды и частоты периодических режимов графоаналитическим методом гармонического баланса
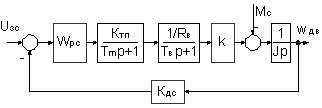
Расчётная структурная схема состоит из последовательно соединённой, преобразованной в единый блок, линейной части ЛЧ и нелинейного элемента НЭ (рис.3.). При этом сигнал задания xo полагается равный нулю, так как расчёт осуществляется для симметричных автоколебаний.
![]()
Условием возникновения периодических режимов в представленной на рис.3 нелинейной системе является основное уравнение гармонической линеаризации:
1+WЛЧ(jw)WНЭ(A)=0, (2)
где WЛЧ(jw) - частотная передаточная функция ЛЧ;
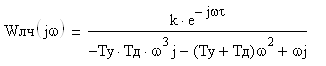 (3)
(3)
Wнэ(А) = q(A) (4)
Поделим обе части уравнения (2) на ![]() :
:
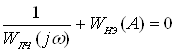 , (2¢)
, (2¢)
Подставим выражения WЛЧ(jw) и WНЭ(A) в формулу (2¢):
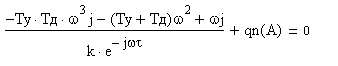
Домножив на знаменатель, получим:
![]() (5)
(5)
Графическое решение уравнения (2) соответствует точкам пересечения кривых WЛЧ(jw) и ZНЭ(A) = -1/ WНЭ(A), по которым из кривой WЛЧ(jw) можно определить частоты wi возможных периодических режимов, а их амплитуды Ai определяют из кривой ZНЭ(A).
Заметим, что при этом могут получаться как устойчивые, так и неустойчивые периодические решения.
Анализ устойчивости этих решений в точках пересечения кривых WЛЧ(jw) и ZНЭ(A) осуществляется по взаимному расположению этих кривых. Рассматривая ZНЭ(A) как параметр D-разбиения из уравнения (2), можно установить, что границей D-разбиения при этом является кривая WЛЧ(jw). Нанеся на эту границу штриховку по известному правилу (слева по ходу при возрастании w), выделяя тем самым область устойчивости (с заштрихованной стороны характеристики ЛЧ системы).
Периодический режим устойчив, если двигаясь по характеристике НЭ в сторону возрастания амплитуды А, переходим из неустойчивой области в устойчивую область D-разбиения, и наоборот.
Заметим, что если кривые WЛЧ(jw) и ZНЭ(A) вообще не пересекаются, то решение уравнения (2) не существует, и автоколебания в заданной нелинейной системе невозможны. Если же указанные кривые имеют точку касания, то автоколебания в этой точке находятся на гране своего возникновения и исчезновения.
Учитывая то, что наименьшего значения функции Z2НЭ и Z1НЭ достигают при значении Re(Zn(A))=-0.05, определим τгр, исходя из того, что Re(WЛЧ(jw)) должно быть также равно -0.05 (WЛЧ (jω) и ZНЭ (А) должны пересекаться на вещественной оси).
Граничным называется минимальное значение ![]() звена запаздывания САУ, при котором автоколебания находятся на границе своего возникновения и исчезновения. При граничном значении τ характеристики ЛЧ и НЭ системы автоматического управления имеют одну общую точку соприкосновения или касания. (кривые WЛЧ (jω) и ZНЭ (А) имеют общую касательную).
звена запаздывания САУ, при котором автоколебания находятся на границе своего возникновения и исчезновения. При граничном значении τ характеристики ЛЧ и НЭ системы автоматического управления имеют одну общую точку соприкосновения или касания. (кривые WЛЧ (jω) и ZНЭ (А) имеют общую касательную).
 τгр=0.00115
τгр=0.00115
Расчёт и построение кривых WЛЧ(jw) и ZНЭ(A) осуществляем с помощью ЭВМ. Построим с помощью ППП Mathcad 2001 кривые WЛЧ (jω) и ZНЭ (А) при различных значениях варьируемого параметра τ.
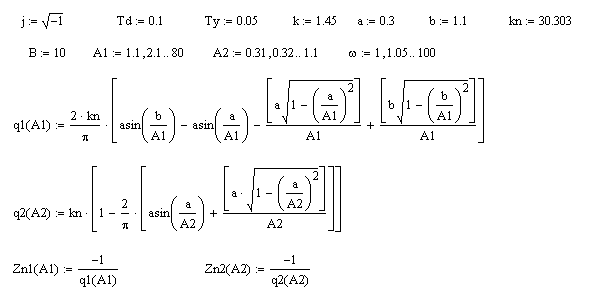
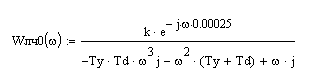
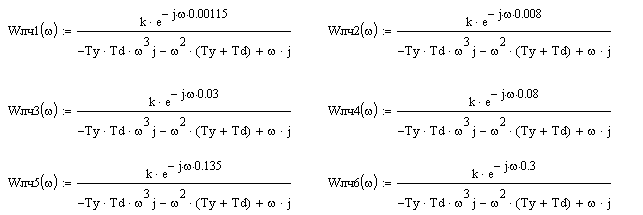
При τ< τгр графики Wлч(jw) и Zнэ(A) пересекаться не будут. Решение уравнения (2) не существует, и автоколебания в нелинейной системе невозможны.
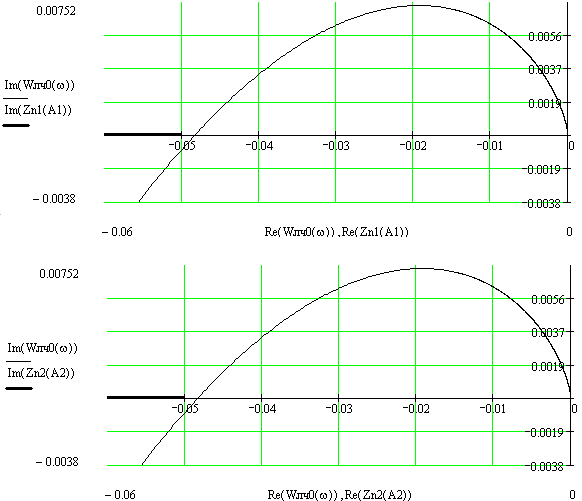
При τ= τгр=0.00115 Wлч(jw) и Zнэ(A) касаются друг друга в точке с координатой -0.05 на вещественной оси, колебания находятся на грани своего возникновения и исчезновения.
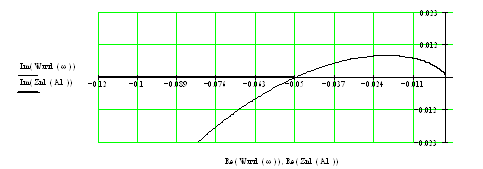

При τ=0.008
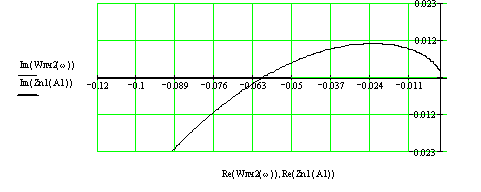

При τ=0.03

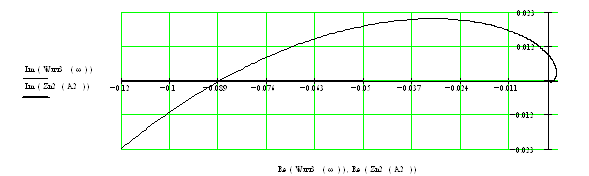
При τ=0.08

 При τ=0.135
При τ=0.135
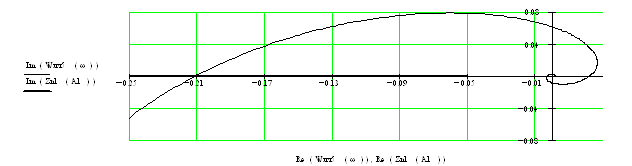
 При τ=0.3
При τ=0.3

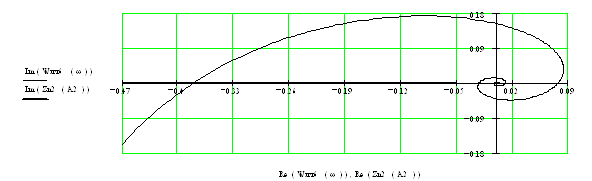 При 0.444>τ>τгр рассматриваемые функции Wлч(jw) и Zнэ(A) имеют одну точку пересечения.
При 0.444>τ>τгр рассматриваемые функции Wлч(jw) и Zнэ(A) имеют одну точку пересечения.
Анализ устойчивости этих решений в точках пересечения кривых WЛЧ(jw) и ZНЭ(A) осуществили по взаимному расположению этих кривых. Периодический режим устойчив, если двигаясь по характеристике НЭ в сторону возрастания амплитуды А, переходим из неустойчивой области в устойчивую область D-разбиения, и наоборот. Проанализировав приведенные выше графики делаем вывод, что при А≥b и 0.444>τ>τгр периодический режим устойчив, а при a≤А≤b неустойчив.
Из полученных графиков найдем значения амплитуды А и частоты ω при различных значения параметра τ.
Ниже представлен расчет при А≥b и τ = 0.00115:

Теперь представим расчеты при a ≤А≤b и τ = 0.3

Остальные значения, приведенные в таблицах 2 и 3, получены по аналогии:
Таблица 2. Таблица 3.
| τ | ω | А≥b |
| 0.00025 | -//- | -//- |
| 0.00115 | 13.904 | 1.166 |
| 0.008 | 12.696 | 1.653 |
| 0.03 | 10.182 | 2.637 |
| 0.08 | 7.333 | 4.569 |
| 0.135 | 5.722 | 6.47 |
| 0.3 | 3.525 | 11.768 |
| τ | ω | a ≤А≤b |
| 0.00025 | -//- | -//- |
| 0.00115 | 13.904 | 1.11 |
| 0.008 | 12.696 | 0.83 |
| 0.03 | 10.182 | 0.579 |
| 0.08 | 7.333 | 0.451 |
| 0.135 | 5.722 | 0.408 |
| 0.3 | 3.525 | 0.364 |
Похожие работы
... имеют отрицательную действительную часть. Поэтому система является устойчивой. 1.7 Исследование установившегося режима САР 1.7.1 Выбор задающих воздействий В следящей системе задающее воздействие заранее не известно—на то она и следящая система. Смотрите ниже по тексту в подразделе Моделирование рабочего режима САР в соответствии с индивидуальным заданием. 1.7.2 Расчет передаточных ...
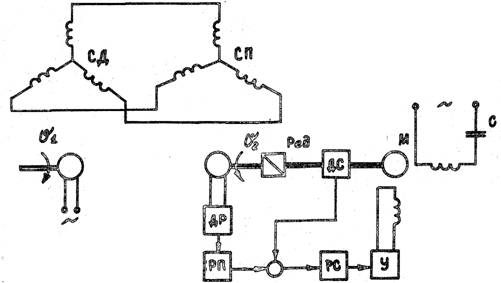
... тепловой нагрузки. Для перехода на дистанционное управление служит блок 14 (БРУ-У), соединенный через пускатель 75 (ПРБ-74) с двигателем 16 (МЭО 25/100), перемещающим P.O. III. Теплота сгорания топлива контролируется датчиком 17 (КГ-7093.01), корректирующий импульс формируется во вторичном приборе 18 (КГ-7093.02). Коррекция задания при изменении тепловой нагрузки осуществляется с помощью блока ...


0 комментариев