Навигация
3. Идеальный газ.
Идеальный газ, идеализированная модель газа; в идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальным газам близки разряженные реальные газы при температурах, далеких от температуры и конденсации. Зависимость давления идеального газа от его температуры и плотности выражается уравнения Клапейрона, (Клаперона-Менделеева уравнение), найденная Б.П. Э. Клапейроном (1834) зависимость между физическими величинами, определяющими состояние идеального газа (давлением р, объемом V, и абсолютной температурой Т): PV=BT, где коэффициент В зависит от массы газов М и его молекулярной массы. Для одного моля идеального газа pV=RT, где R-газовая постоянная. Если молярная масса газа μ, то pV=M/μ *RT.
4. Реальный газ.
Реальный газ, отличается от идеального газа существованием взаимодействия между его частицами (молекулами, атомами). При малых плотностях наличие межмолекулярного взаимодействия учитывается вириальным уравнением состояния реального газа: pV=RT[1+B (T)/υ+C(T)/υ2+…], где р - давление, υ – молярный объем, Т – абсолютная температура, R – газовая постоянная, В(Т), С(Т) и так далее – вириальные коэффициенты, зависящие от температуры и характеризующие парные, тройные и так далее взаимодействия частиц в газе. Существуют и другие полуэмпирические и теоретические уравнения состояния реальных газов, например: уравнение Ван дер Ваальса (нидерландского физика), предложенное Ван дер Вальсом (1873г) уравнение состояния реального газа, учитывающее конечность объема молекул и наличие межмолекулярных сил притяжения; для одного моля газа имеет вид: (р+а/V2) (v-b)=RT, где р – давление, V – объем одного моля, T – абсолютная температура, R – универсальная газовая постоянная, a и b постоянные, характеризующие взаимодействие молекул данного вещества. Третье начало термодинамики: по мере приближения температуры к 0K. Энтропия всякой равновесной системе при изотермических процессах перестает зависеть от каких-либо термодинамических параметров состояния и в пределе (T=0K) принимает одну и туже для всех систем постоянную величину, которую можно принять равной нулю. Третье начало предсказывает вырождение идеальных азов при низкой температуре. Как показало развитие квантовой статистики, такое вырождение действительно имеет место. Оно указывает на недостаточность классической механики и основанной на ней классической статистики в области низких температур. Квантовая статистика показывает, что третье начало термодинамики является микроскопическим проявлением квантовых свойств реальных систем при низких температурах. Свойства реальных систем изучались экспериментально.
5. Молекулярно – кинетическая теория критических явлений.
Вскоре после открытия закона Бойля – Мариотта (произведение объема данной массы идеального газа на его давление постоянно при постоянной температуре; установлен независимо Р. Бойлем (1660г) и Э. Мариоттом (1676г)) были обнаружены отклонения от него: нидерландский физик Мартин Ван Марум установил, что при давлении 7 атмосфер газообразный аммиак переходит в жидкое состояние; примерно тогда же Лавуазье отметил роль охлаждения в изменении состояния газов. В середине прошлого века появились попытки учесть эти отклонения количественно, чтобы ввести поправки, но все они были случайными и не связывались с критическими состояниями газов. Ван-дер-Ваальс показал глубинную связь между жидким и газообразным состояниями вещества, объяснил их непрерывный переход друг в друга и развил молекулярно-кинетическую теорию критических явлений. Его теория позволила предсказать существование неустойчивых состояний вещества. После создания Гиббсом статистической механики наглядная теория Ван-дер-Ваальса была переведена на строгий математический язык. Гиббс дал развернутое изложение метода термодинамических потенциалов и его применение к анализу равновесия. С позиции своего метода он единым образом исследовал законы образования новой фазы, дал знаменитое правило фаз (в термодинамике: число равновесно сосуществующих в какой либо системе фаз не может быть больше числа образующих эти фазы компонентов плюс, как правило, 2). Установлено Дж. У. Гиббсом в 1873-1876гг, рассмотрел поверхностные и электрохимические явления, многокомпонентные системы и тому подобные. Развивая метод Гиббса, Дюгем в своих работах ввел термин «термодинамический потенциал». Гиббс пришел к идее введения таких функций после исследования поведения функции (Е-ТS+pV), когда заметил, что условие устойчивого равновесия сводится к равенству б(Е-ТS+рV)=0. Экстремальные значения этой функции оказались необходимыми и достаточными условиями равновесия систем при изобарно - изотермических процессах. В последствии эту функцию назвали изобарно – изотермическим потенциалом, или потенциалом Гиббса. Затем Гиббс установил, что термодинамические свойства системы можно описать еще тремя функциями, обладающими свойствами потенциалов – внутренней энергией (диабатический потенциал) и тепловой функцией (энтальпия). В химической термодинамике важен и химический потенциал, введенный Гиббсом.
С точки зрения статистической механики вывод уравнения состояния сводится к нахождению новой функции состояния свободной энергии F=E-TS как функции параметров p,T,V. Тогда уравнение состояния находится как p=-I∂I±I∂VIT. Нужно было найти свободную энергию системы, вычислив соответствующий интервал, что было непростой задачей. Гиббс понимал, что для полного описания системы, даваемого термодинамическими потенциалами, нужно знание молекулярной структуры и характера взаимодействия частиц. Поэтому он разработал метод нахождения статистических аналогов для изотермического и химического потенциалов. Метод Гиббса был пригоден для любых систем, но математические трудности того времени не позволяли уйти от идеализированных моделей.
Похожие работы
... равны удельным значениям энтропии, взятой с обратным знаком, и объеме: (4.30) Если в точках, удовлетворяющих фазовому равновесию: , первые производные химического потенциала для разных фаз испытывают разрыв: , (4.31) говорят, что термодинамическая система испытывает фазовый переход I-го рода. Для фазовых переходов первого рода характерно наличие срытой теплоты фазового перехода, ...
... от переподъемов, нулевую и максимальную защиты. - предусматривать остановку сосудов в промежуточных точках ствола. световую сигнализацию о режимах работы подъемной установки в здании подъемной машины, у оператора загрузочного устройства, у диспетчера. Современные регулируемые электроприводы постоянного тока для автоматизированных подъемных установок выполняют на основе двигателей постоянного ...
... = 44,5 см, c = 12 см, а=20 см, l=8 см. Силовое действие магнитной системы оценивалось по величине равной произведению модуля поля Н на его градиент. Было получено, что распределение модуля поля Н рассматриваемой нами магнитной системы характеризуется ярко выраженной угловой зависимостью. Поэтому расчет модуля поля Н проводился с шагом в 1° для точек, расположенных на двух разных дугах для всего ...
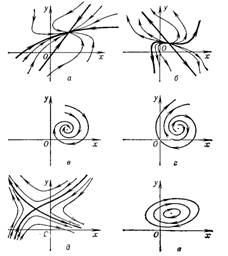
... системы состоит в получении ее “фазового портрета” (Волькенштейн, 1978). Он дает возможность выявить стационарные состояния системы и характер ее динамики при отклонении от них. Метод фазовых портретов применяется в технике для анализа и предсказания поведения физических систем различной сложности и в математической экологии для анализа динамики численности популяций (Волькенштейн, 1978; Свирежев ...

0 комментариев