Навигация
Часов, 0 минут, 34.703 секунд
0 часов, 0 минут, 34.703 секунд.
Приложение
1) % Программа синтеза управления системы самонаведения (рассматривается часть % системы) методами обратных задач динамики с использованием метода % матричных операторов (линейная модель)
close all;
clear all;
clc;
my_tic;
global Nl;
global U tgl;
global Krp Trp Ksn Tsn DZsn V G Kdy Kv mu Tc Xmax;
%% 1. Эталонный закон изменения угла teta(t)
% Время наведения
fId = fopen('t_navedenija.dat','r');
t_f = fread(fId,inf,'real*8')';
fclose(fId);
Nt_f = length(t_f);
h_t_f = t_f(2)-t_f(1);
T = t_f(Nt_f);
% угол theta(t)
fId = fopen('theta_navedenija.dat','r');
theta_f = fread(fId,[1 Nt_f],'real*8');
fclose(fId);
% расстояние до цели
fId = fopen('r_navedenija.dat','r');
r_f = fread(fId,[1 Nt_f],'real*8');
fclose(fId);
fprintf('1. Эталонный закон изменения угла teta(t)\n');
fprintf('Число точек квантования по времени: Nt = %i;\n',Nt_f);
fprintf('Шаг квантования: h_t = %f c;\n',h_t_f);
fprintf('Время поражения цели: T = %f c;\n',T);
fprintf('\n');
my_plot2(t_f,theta_f,'t, c','theta(t), рад');
my_plot2(t_f,r_f,'t, c','r(t), м');
% пересчет на больший шаг квантования
Nt = 64;
h_t = T/(Nt-1);
t = 0: h_t: T;
theta = spline(t_f,theta_f,t);
r = spline(t_f,r_f,t);
my_plot2(t,theta,'t, c','theta(t), рад');
my_plot2(t,r,'t, c','r(t), м');
%% 2. Параметры системы
% Числовые значения параметров системы самонаведения
Krp = 1; %
Trp = 0.33; % с
Xmax = 24*pi/180; % рад
Ksn = 0.283; % рад/с
Tsn = 0.155; % с
DZsn = 0.052; %
V = 70*9.81; % м/с
G = 9.81; % м/с^2
Kdy = 0.14; %
Kv = 1.2; % c
mu = 0.115; % с
Tc = 3.05; % с
fprintf('2. Числовые значения параметров системы самонаведения\n');
fprintf('Krp = %f;\n',Krp);
fprintf('Trp = %f, с;\n',Trp);
fprintf('Xmax = %f, рад;\n',Xmax);
fprintf('Ksn = %f, рад/с;\n',Ksn);
fprintf('Tsn = %f, с;\n',Tsn);
fprintf('DZsn = %f;\n',DZsn);
fprintf('V = %f, м/с;\n',V);
fprintf('G = %f, м/с^2;\n',G);
fprintf('Kdy = %f;\n',Kdy);
fprintf('Kv = %f, c;\n',Kv);
fprintf('mu = %f, с;\n',mu);
fprintf('Tc = %f, с;\n',Tc);
fprintf('\n');
%% 3. Формирование ортонормированного базиса
Nl = Nt;
setsize(Nl);
settime(T);
Ai = mkint; % оператор интегрирования
Ad = inv(Ai); % оператор дифференцирования
Ae = eye(Nl); % единичная матрица
fprintf('3. Базис - функции Уолша\n');
fprintf('Число элементов: Nl = %i;\n',Nl);
pr_matrix(Ai,'Оператор интегрирования Ai')
pr_matrix(Ad,'Оператор дифференцирования Ad')
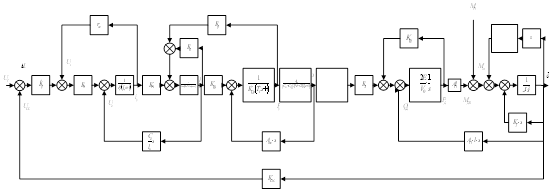
%% 4. Расчет операторов системы
Arp = inv(Trp*Ae+Ai)*(Krp*Ai);
Asn = inv(Tsn^2*Ae+2*DZsn*Tsn*Ai+Ai*Ai)*(Ksn*Ai*Ai);
Aos1 = Kv*mu*Tc*Ad*Ad+Kv*(mu+Tc)*Ad+Kv*Ae;
Aos2 = (Kdy*V/G)*Ae;
Apr = Asn*Arp;
Aos = Aos1+Aos2;
As = inv(Ae+Aos*Apr)*Apr;
As = Ai*As;
fprintf('4. Матричные операторы системы\n');
pr_matrix(Arp,'Arp');
pr_matrix(Asn,'Asn');
pr_matrix(Aos1,'Aos1');
pr_matrix(Aos2,'Aos2');
pr_matrix(Apr,'Apr');
pr_matrix(Aos,'Aos');
pr_matrix(As,'As');
%% 5. Расчет спектральной характеристики эталонного выхода
Ctheta = fwht(theta');
fprintf('5. СХ эталонного выхода\n');
pr_matrix(Ctheta,'Ctheta');
%% 6. Синтез входного сигнала
Cu_0 = zeros(Nl,1);
fprintf('Начальные значения искомых коэффициентов\n');
pr_matrix(Cu_0,'Cu_0');
oshibka = sqrt((As*Cu_0-Ctheta)'*(As*Cu_0-Ctheta));
fprintf('Oshibka_0 = %e\n',oshibka);
my_function = @(Cu)sqrt((As*Cu-Ctheta)'*(As*Cu-Ctheta));
% optimset('Display','iter','NonlEqnAlgorithm','gn','TolFun',1e-8,...
Cu = fsolve(my_function,Cu_0,...
optimset('NonlEqnAlgorithm','gn','TolFun',1e-8,...
'TolX',1e-8,'MaxFunEvals',50000,'MaxIter',50000));
% Cu = inv(As)*Ctheta;
fprintf('Оптимальные значения искомых коэффициентов\n');
pr_matrix(Cu,'Cu_opt');
oshibka = sqrt((As*Cu-Ctheta)'*(As*Cu-Ctheta));
fprintf('Oshibka_0 = %e\n',oshibka);
U = iwht(Cu)';
tgl = t;
my_plot2(t,U,'t, c','U(t)');
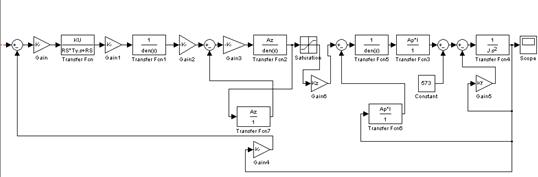
%% 7. Анализ полученных результатов (метод Рунге-Кутта (ode45))
[tt,yy] = ode45(@ode_navedenija1,t,[0 0 0 0]);
theta_rr = yy(:,1)';
my_plot2(t,[theta;theta_rr],'t, c','theta(t), рад','',['эталонный ';'реальный ']);
my_toc;
2) второстепенные программы:
function dy = ode_navedenija1(t,y);
global U tgl;
global Krp Trp Ksn Tsn DZsn V G Kdy Kv mu Tc Xmax;
a32 = -1/(Tsn^2);
a33 = -2*DZsn/Tsn;
a3f = Ksn/(Tsn^2);
a42 = -(Krp/Trp)*(Kv-Kv*mu*Tc/(Tsn^2)+Kdy*V/G);
a43 = -(Krp/Trp)*(Kv*(mu+Tc)-2*Kv*mu*Tc*DZsn/Tsn);
a44 = -1/Trp;
a4f = -(Krp/Trp)*Kv*Ksn*mu*Tc/(Tsn^2);
b4 = Krp/Trp;
u = spline(tgl,U,t);
dy = zeros(4,1);
dy(1) = y(2);
dy(2) = y(3);
y4 = y(4);
dy(3) = a32*y(2)+a33*y(3)+a3f*y4;
dy(4) = b4*u+a42*y(2)+a43*y(3)+a44*y(4)+a4f*y4;
Похожие работы
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
... относительности (теории тяготения). Исходя из изложенного, в механике пользуются единым термином «масса», определяя массу как меру инертности тела и его гравитационных свойств. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ. РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ Для решения задач динамики точки будем пользоваться одной из следующих двух систем уравнений ...
... закономерностям, независимо от наших знаний о природе явлений. Всякое следствие имеет свою причину. Как и все остальное в физике, понятие детерминизма менялось по мере развития физики и всего естествознания. В 19-м веке теория Ньютона окончательно оформилась и установилась. Существенный вклад в ее становление внес П.С.Лаплас (1749 - 1827). Он был автором классических трудов по небесной механике и ...
... . 5. Получены длительные непрерывные ряды наблюдений интенсивности потока и азимутальных распределений СДВ атмосфериков, которые позволили проследить динамику грозовой активности в мировых грозовых центрах. 5.1. Морской мониторинг показал, что основной вклад в мировую грозовую активность дают континентальные и островные грозовые центры. Вариации интенсивности потока импульсов хорошо ...
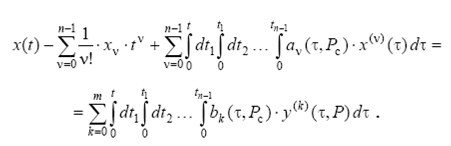
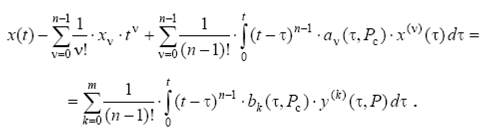
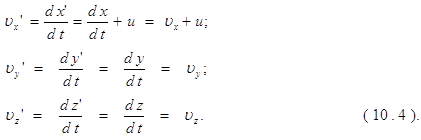
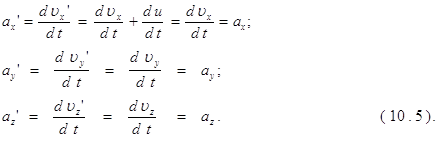
0 комментариев