Навигация
САМООРГАНІЗАЦІЯ РІЗНИХ СІСТЕМ І СИНЕРГЕТІКА
2.2 САМООРГАНІЗАЦІЯ РІЗНИХ СІСТЕМ І СИНЕРГЕТІКА
Перехід від хаосу до порядку, що відбувається при зміні значень параметрів від до критичних до надкритичних, змінює симетрію системи . По цьому такий перехід аналогічний термодинамічним фазовим переходам . Переходи в нерівноважних процесах називаються кінетичними фазовими переходами. У близи нерівноважних фазових переходів не існує несуперечливого макроскопічного опису. Флуктуації такі ж важливі, як і середнє значенні. Наприклад, макроскопічні флуктуації можуть приводити до нових типів не устойчивостей.
Отже, в далечіні від рівноваги між хімічною, кінетичною і просторово-часовою структурою реагуючих систем існує несподіваний зв'язок . Правда, взаємодія, що визначають взаємодію констант швидкостей і коефіцієнтів перенесення, обумовлені короткодіючими силами (силами валентності, водневими зв'язками і силами Ван-Дер-Ваальса). Проте вирішення відповідних рівнянь залежать, крім того, від глобальних характеристик. Для виникнення дисипативних структур зазвичай потрібний, щоб розміри системи перевищували деяке критичне значення - складну функцію параметрів, що описують реакційно-дифузійні процеси . Ми можемо по цьому стверджувати, що хімічні нестійкості задають подальший порядок, за допомогою якого система діє як ціле .
Якщо врахувати дифузію, то математичне формулювання проблем, пов'язаних з дисипативними структурами, зажадає вивченні диференціальних рівнянь в приватних похідних. Дійсно, еволюція![]() концентрації компонент Х з часом визначається рівнянням вигляду
концентрації компонент Х з часом визначається рівнянням вигляду
![]() (2.4)
(2.4)
де перший член дає внесок хімічних реакцій в зміні концентрації Хi і зазвичай має простий полиноминальный вигляд, а другий член означає дифузію уздовж осі r.
Дійсно вражаюче, як багато різноманітних явищ описує реакційно-дифузне рівняння (2.4 ), по цьому цікаво розглянути ² основне рішення, яке б відповідала термодинамічній гілці . Інші рішення можна було б отримувати при не послідовних устойчивостях, що виникають у міру видалення від стану рівноваги. Нестійкості такого типу зручно вивчати методами теорії біфуркації [Николіс і Прігожін, 1977]. В принципі, біфуркація є щось інше, як виникнення при деякому критичному значенні параметра нового вирішення рівнянь . Припустимо, що ми маємо хімічну реакцію, відповідну кінетичному рівнянню [ Маклейн і Уоліс, 1974] .
d X ¾ = а X (X-R) (2.5)¾ d t
Ясно що при R < 0 існує тільки одне рішення, незалежне від часу, X = 0. У точці R = 0 відбувається біфуркація, і з'являється нове рішення X = R.
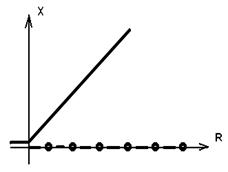
Мал. 2.3. Біфуркационная диограмма для рівняння ( 2.5.)
Суцільна лінія відповідає стійкій гілці
крапки - нестійкої гілки
Аналіз стійкості в лінійному наближенні дозволяє перевірити, що рішення X = 0 під час переходу через R = 0 стає нестійким, а рішення X = R - стійким . Загалом випадки при зростанні деякого характеристичного параметра р відбуваються послідовні біфуркації . На малюнку 2.4. показано єдине рішення при р = р1, але при р = р2 єдиністю поступається місце множинним рішення.
Цікаво відзначити, що біфуркація в деякому розумінні вводить у фізику і в хімію, історію - елемент, який раніше вважався прерогативою наук що займаються вивченням біологічним, суспільних і культурних явищ .
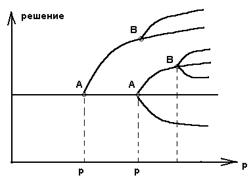
Мал. 2.4. Послідовні біфуркації:
А і А1 - точки первинних біфуркацій з термодинамічній гілці
У і В1 - точки вторинної біфуркації
Відомо, що при зміні параметрів, що управляють, в системі спостерігаються різноманітні перехідні явища. Виділимо тепер з цих спостережень певні загальні риси, характерні для великого числа інших переходів у физико хімічних системах.
З цією метою представимо графічно (мал. 2.5) залежність вертикальною компоненти швидкості перебігу рідини в деякій певній крапці від зовнішнього обмеження, або, в більш загальному вигляді, залежність змінної стан системи Х (або х = Х - Хs ) від параметра, що управляє l. Таким чином ми отримаємо графік, відомий під назвою бифуркационной діаграми.
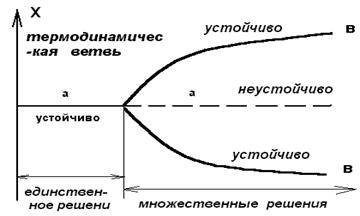
Мал. 2.5. Біфуркаційна діаграма:
а - стійка частина термодинамічної гілки
а1 - не стійка частина термодинамічної гілки
в1,в2 - дисипативні структури, народжені в
надкритичній області .
При малих значення l можливо лише одне рішення, відповідне поляганню спокою в бенаровському експерименті. Воно є безпосередню екстраполяцію термодинамічної рівноваги, і подібно рівноважне, що характеризується важливою властивістю - асимптотичною стійкістю, оскільки в цій області система здатна гасити внутрішні флуктуації або зовнішнє обурення . З цієї причини таку гілку станів ми називатимемо термодинамічною гілкою. Під час переходу критичного значення параметраl, позначеного lз на малюнку 2.5., що перебувають на цій гілці стає нестійкими, оскільки флуктуації або малі зовнішні обурення вже не гасяться . Діючи подібно до підсилювача, система відхиляється від стаціонарного стану і переходить до нового режиму, у разі бенаровського експерименту відповідному стану стаціонарної конвекції. Обидва цих режиму зливаються при = lз і розрізняються при > з . Це явище називається біфуркацією . Легко зрозуміти причини, по яких це явище слід асоціювати з катастрофічними змінами і конфліктами. Насправді, у вирішальний момент переходу система повинна зробити критичний вибір ( у околиці = з ), що в завданні Бенара пов'язане з виникненням право- або лівообертальних осередків в певній області простору ( мал. 2.5., гілки в1 або в2 ).
Поруч з рівноважним станом стаціонарний стан асимптотичних стійкий (по теоремі про мінімальне виробництво ентропії ), по цьому через безперервність ця термодинамічна гілка тягнеться у всій докритичній області. Досягши критичного значення термодинамічна гілка може стати нестійкою, так що будь-яке, навіть мале обурення, перекладає систему з термодинамічної гілки в новий стійкий стан, який може бути впорядкованим. Отже, при критичному значенні параметром відбулася біфуркація і виникла нова гілка рішень і, відповідно, новий стан. У критичній області, таким чином, подія розвивається по такій схемі
Флуктуація ® Біфуркація
нерівноважний фазовий перехід ®
Народження впорядкованої структури
Біфуркація в широкому розумінні - придбанні нової якості рухами динамічної системи при малій зміні її параметрів ( виникнення при деякому критичному значенні параметра нового вирішення рівнянь ) . Відзначимо, що при біфуркації вибір наступного стану носить суто випадковий характер, так що перехід від одного необхідного стійкого стану до іншого необхідного стійкому стану проходить через випадкове (діалектика необхідного і випадкового) . Будь-який опис системи, що зазнає біфуркацію, включає як детерміністичний, так і імовірнісний елементи, від біфуркації до біфуркації поведінці системи детерміновано, а в околиці точок біфуркації вибір подальшого шляху випадковий. Проводячи аналогію з біологічною еволюцією можна сказати, що мутації - це флуктуації, а пошук нової стійкості грає роль природного відбору. Біфуркація в деякому розумінні вводить у фізику і хімію елемент історизму - аналіз стану в1, наприклад, має на увазі знання історії системи, що пройшла біфуркацію.
Загальна теорія процесів самоорганізації відкритих сильно не рівноважних системах розвивається на основі універсального критерію еволюції Прігожіна-Гленсдорфа. Цей критерій є узагальненням теореми Прігожіна про мінімальне виробництво ентропії. Швидкість виробництва ентропії, обумовлена зміною термодинамічних сил Х, згідно цьому критерію підкоряється умові
dx P / t £ 0 (2.6)£
Ця нерівність не залежить не від яких припущень про характер зв'язків між потоками і силами в умовах локальної рівноваги і носить по цьому універсальний характер . У лінійній області нерівність (2.6. ) переходить в теорему Прігожіна про мінімальне виробництво ентропії . Отже, в неравновестной системі процеси йдуть так, тобто система еволюціонує таким чином, що швидкість виробництва ентропії при зміні термодинамічних сил зменшується (або рівна нулю в стаціонарному стані).
Впорядковані структури, які народжуються далеко від рівноваги, відповідно до критерію (2.6.) і є диссипативні структури.
Еволюція біфуркації і подальшої самоорганізації обумовлено, таким чином, відповідними не рівноважними обмеженнями.
Еволюція змінних Х описуватиметься системою рівнянь
![]() (2.7)
(2.7)
де функції F як завгодно складним чином можуть залежать від самих змінних Х і їх просторових похідних координат r і часу t . Крім того, ці функції буду залежать від параметрів, що управляють, тобто тих характеристик, що змінюються, які можуть сильно змінити систему . На перший погляд здається очевидним, що структура функції { F } буде сильна визначаться типом відповідної даної системи . Проте, можна виділити деякі основні універсальні риси, незалежні від типу систем.
Вирішення рівняння (2.7), якщо немає зовнішніх обмежень, повинні відповідати рівновазі при будь-якому виді функції F . Оскільки рівноважний стан стаціонарний, то
Fi ({Xрав},равl ) = 0 (2.8)l
У більш загальному випадку для нерівноважного стану можна аналогічно написати умову
Fi ({X},l) = 0 (2.9)l
Ці умови накладають певні обмеження універсального характеру, наприклад, закони еволюції системи повинні бути такими, щоб виконувалася вимога позитивності температури або хімічної концентрації, що отримуються як вирішення відповідних рівнянь.
Іншою універсальною межею є нелінійним . Хай, наприклад деяка єдина характеристика системи задовольняє рівнянню
![]() (2.10)
(2.10)
де до - деякий параметр, l - зовнішні обмеження, що управляють . Тоді стаціонарний стан визначається з наступного рівняння алгебри
l - kX = 0 (2.11)l
звідки
Xs = l / до (2.12)l
У стаціонарному стані, таким чином, значенні характеристики, наприклад, концентрації, лінійно змінюється залежно від значень обмеженняl, що управляєl, і є для кожного єдиний стан Хs . Абсолютно однозначно можна передбачити стаціонарне значення Х при будь-якомуl,если мати хоч би два експериментальні значення Х(l). Керуючий параметр може, зокрема, відповідати ступеню віддаленості системи від рівноваги . Поведінка в цьому випадку системи дуже схожі на рівновазі навіть за наявності сильно нерівноважних обмежень.
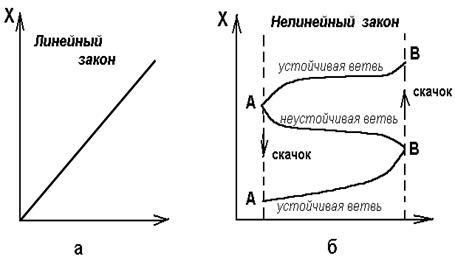
Мал. 2.6. Ілюстрація універсальної межі нелінійності в самоорганізації структур
Якщо ж стаціонарне значення характеристики Х не лінійно залежить від обмеження, що управляє, при деяких значеннях, то при одному і тому ж значенні є декілька різних рішень . Наприклад, при обмеженнях система має три стаціонарні рішення, малюнок 2.6.в. Така універсальна відмінність від лінійної поведінки наступає при досягненні параметром, що управляє, деякого критичного значення l - виявляється біфуркація. При цьому в нелінійній області невелике збільшення може привести до неадекватно сильному ефекту - система може зробити стрибок на стійку гілку при невеликій зміні поблизу критичного значенняl, малюнок 2.6.в. Крім того з перебувань на гілці А1в можуть відбуватися переходи Ав1 ( або навпаки ) навіть раніше, ніж будуть досягнуті полягання В або А, якщо обурення накладаються на стаціонарний стан, більше значення, відповідного проміжній гілці А В . Обуреннями можуть служити або зовнішня дія або внутрішні флуктуації в самій системі. Таким чином, системі з множинними стаціонарними станами властиво універсально властивостям внутрішньо збудливість і мінливості скачкам.
Виконання теореми по мінімально виробництві ентропії в лінійній області, а, як узагальнення цієї теореми, виконання універсального критерію (2.6.) і в лінійній, і в нелінійній області гарантують стійкість стаціонарних нерівноважних станів. В області лінійності необоротних процесів виробництво ентропії грає таку ж роль, як термодинамічні потенціали в рівноважній термодинаміці. У нелінійній області величина dP / dt не має якого або загальної властивості, проте, величина dx P/dt задовольняє нерівності загального характеру (2.6.), яка є узагальненням теореми про мінімальне виробництво ентропії.
Похожие работы
... а потім дві незалежні частоти. Хаотичний режим, що характеризується суцільним спектром, з'являвся відразу слідом за квазіперіодичною двохчастотною течією. Розділ 5. Застосування понять фізики відкритих систем до моделювання обробки інформації. Знання основних закономірностей утворення структур в активних середовищах, а також у мережах, що складаються з великої кількості активних елементів, ...
... это то, что устраняет неопределенность, количество "снятой" неопределенности. Тенденция к определенности, к повышению информативности - процесс негэнтропийный (процесс с обратным знаком). Термин "самоорганизующаяся система" ввел кибернетик У. Росс Эшби для описания кибернетических систем. Для самоорганизующихся систем характерны: 1) Способность активно взаимодействовать со средой, изменять ...
... проблемы, где соответствующей проверки не производилось. При обнаружении расхождений так создаваемых концепций с реально наблюдаемыми явлениями неизбежно возникало недоумение, граничащее с попытками отрицания самой возможности познания окружающего мира. Современное естествознание характеризуется лавинообразным накоплением нового фактического материала и возникновением множества новых дисциплин ...
... субъекта (Юм), априорным формам мышления (Кант), целевым установкам личности (прагматизм), интерсубъективным конвенциям (А. Пуанкаре) и др. Фундаментальными проблемами в данной сфере выступали в классической философии проблема критерия И., трактовка которого соответствовала принятому определению И. (от эйдотического образца у Платона до Божественной Мудрости у Фомы Аквинского, с одной стороны, и ...
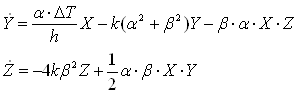
0 комментариев