Навигация
3.3 ДИНАМІКА ПОПУЛЯЦІЇ
Про розповсюдження і чисельність видів була зібрана велика інформація. Макроскопічною характеристикою, що описує популяцію, може бути число особин в популяції . Це число грає роль параметра порядку. Якщо різні види підтримуються загальним харчовим ресурсом, то починається міжвидова боротьба, і тоді застосуємо принцип Дарвіна: виживає найбільш пристосований вигляд. (Не можна не відзначити сильну аналогію, що існує між конкуренцією лазерних мод і міжвидовою боротьбою). Якщо є однотипні харчові ресурси, то стає можливим співіснування видів. Чисельність видів може бути схильна до тимчасових коливань.
ОДИН ВИГЛЯД.
Розглянемо спочатку одну популяцію з числом особин в ній n . За наявності харчових ресурсів А особини розмножуються з швидкістю :
![]()
і гинуть з швидкістю :
![]()
Тут до і d - деякі коефіцієнти народжуваності і смертності, в загальному випадку залежне від параметрів зовнішнього місця існування. Якби кількість їжі була необмежено, то еволюційне рівняння виглядало б так:
![]()
Введемо позначення a = kA - d
Воно було б лінійним і описувало б необмежене експериментальне зростання (при kA > d), або експериментальну загибель (при kA < d) популяції.
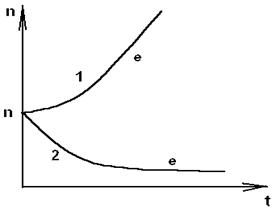
Мал. 3.4 Крива 1: Експоненціальне зростання; >a0, kA>d
Крива 2: Експоненціальна загибель; >a0, kA>d.
У загальному випадку, проте, харчові ресурси обмежені, так що швидкість споживання їжі
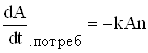
Разом з тим в загальному випадку можливе відновлення харчових ресурсів з швидкістю :
![]()
Тут, звичайно, розглянутий боковий випадок збереження повної кількості органічної речовини
A + n = N = const
N - здатність місця існування підтримувати популяцію.
Тоді з урахуванням A = N - n вийде наступне рівняння еволюції популяції одного вигляду (логістичне рівняння Ферхюльста ) :
![]() (3.17)
(3.17)
Вирішимо рівняння (3.17) аналітично, перепишемо його таким чином
![]() позначимо kN - d = k1
позначимо kN - d = k1
Отримаємо :
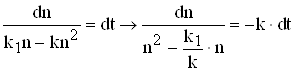
Скористаємося ![]() табличним інтегралом
табличним інтегралом 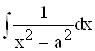 ,полученное рівняння прийме вигляд :
,полученное рівняння прийме вигляд :
![]()
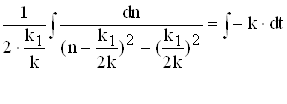
вирішимо це рівняння, перетворюючи
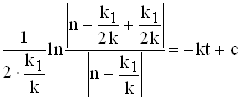

скоротимо отриманий вираз на до, і перенесемо змінну k1 в праву частину, отримаємо
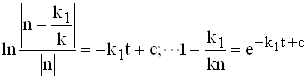
звідси n(t) ® ![]()
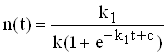
Початкові умови :
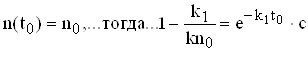
Звідки
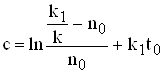
Підставляючи з в рішення, отримаємо рівняння в наступному вигляді
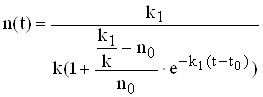
раніше ми означали, що ![]() підставляємо і перетворюваний
підставляємо і перетворюваний
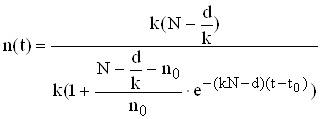
скоротимо на до - коефіцієнт народжуваності, остаточно отримаємо вирішення рівняння (3.17)

Отже, отримано аналітичне вирішення логістичного рівняння - це рішення указує на те, що зростання популяції зупиняється на деякому кінцевому стаціонарному рівні:
![]()
тобто параметр n1 указує висоту плато насичення, до якого прагне n(t) з часом .
Параметр n0 указує початкове значення чисельності одного виду популяції : n0 = n(t0) . Дійсно ![]() ,то є n1 - гранична чисельність вигляду в даному місці існування . Інакше кажучи, параметр n1 характеризує ємкість середовища по відношенню до даної популяції . І нарешті, параметр (kN - d) задає крутизну початкового зростання.
,то є n1 - гранична чисельність вигляду в даному місці існування . Інакше кажучи, параметр n1 характеризує ємкість середовища по відношенню до даної популяції . І нарешті, параметр (kN - d) задає крутизну початкового зростання.
Відзначимо, що при малій початковій чисельності n0 (початкове число особини) початкове зростання популяцій буде майже експоненціальним
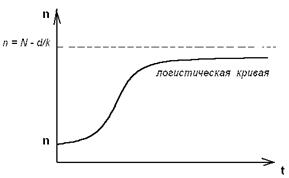
Мал. 3.5. Логістична крива.
(еволюція популяції одного вигляду)
Вирішення рівняння (3.17) можна представити за допомогою логістичної кривої (мал. 3.5) . Еволюція повністю детермінована . Популяція перестає рости, коли ресурс середовища виявляється вичерпаним.
Самоорганізація - при обмеженому харчовому ресурсі. Підкреслимо, що при описі даної біологічної системи використовують понятійний і фізико-математичний апарат з нелінійної нерівноважної термодинаміки.
Може трапиться, проте, що завжди за подіями, не керованими в рамках моделі, в тому ж середовищі з'явиться, спочатку в малих кількостях, новий вигляд (що характеризуються іншими екологічними параметрами к,N і d) . У зв'язку з такою екологічною флуктуацією виникає питання про структурну стійкість: новий вигляд може або зникнути, або витіснити первинних мешканців.
Користуючись лінійним аналізом стійкості, не важко показати, що новий вигляд витісняє старі тільки в тому випадку, якщо
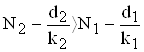
Послідовність, в якій види заповнюють екологічну нішу, представлена на малюнку 3.6.
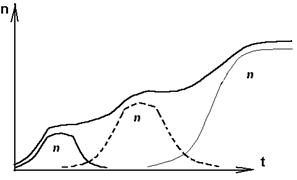
Мал. 3.6. Послідовне заповнення екологічної ніші різними видами .
Ця модель дозволяє додати точним кількісний сенс твердженню про те, що «виживає найбільш пристосований», в рамках завдання про заповнення заданої екологічної ніші .
Похожие работы
... а потім дві незалежні частоти. Хаотичний режим, що характеризується суцільним спектром, з'являвся відразу слідом за квазіперіодичною двохчастотною течією. Розділ 5. Застосування понять фізики відкритих систем до моделювання обробки інформації. Знання основних закономірностей утворення структур в активних середовищах, а також у мережах, що складаються з великої кількості активних елементів, ...
... это то, что устраняет неопределенность, количество "снятой" неопределенности. Тенденция к определенности, к повышению информативности - процесс негэнтропийный (процесс с обратным знаком). Термин "самоорганизующаяся система" ввел кибернетик У. Росс Эшби для описания кибернетических систем. Для самоорганизующихся систем характерны: 1) Способность активно взаимодействовать со средой, изменять ...
... проблемы, где соответствующей проверки не производилось. При обнаружении расхождений так создаваемых концепций с реально наблюдаемыми явлениями неизбежно возникало недоумение, граничащее с попытками отрицания самой возможности познания окружающего мира. Современное естествознание характеризуется лавинообразным накоплением нового фактического материала и возникновением множества новых дисциплин ...
... субъекта (Юм), априорным формам мышления (Кант), целевым установкам личности (прагматизм), интерсубъективным конвенциям (А. Пуанкаре) и др. Фундаментальными проблемами в данной сфере выступали в классической философии проблема критерия И., трактовка которого соответствовала принятому определению И. (от эйдотического образца у Платона до Божественной Мудрости у Фомы Аквинского, с одной стороны, и ...
0 комментариев