Навигация
3.1 ОСЕРЕДКИ БЕНАРА
Для того, щоб експериментально вивчити структури, досить мати сковороду, трохи масла і якою ні будь дрібний порошок, щоб було помітно рух рідини . Наллємо в сковороду масло з розмішаним в нім порошком і підігріватимемо її знизу (мал. 3.1)
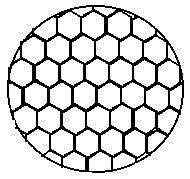
Мал. 3.1. Конвективні осередки Бенара
Якщо дно сковороди плоске і нагріваємо ми її рівномірно, то можна вважати, що у дна і на поверхні підтримуються постійні температури, знизу - Т1, зверху - Т2 . Поки різниця температури DТ = Т1 - Т2 невелика, частинки порошку нерухомі, а отже, нерухома і рідина .
Плавно збільшуватимемо температуру Т1. Із зростанням різниці температур до значення DТc спостерігається все та ж картина, але коли DТ > DТc, все середовище розбивається на правильні шестигранні осередки (див. Мал. 3.1) в центрі кожної з яких рідина рухається вгору, по кроях вниз . Якщо узяти іншу сковороду, то можна переконатися, що величина виникаючих осередків практично не залежить від її форми і розмірів . Цей чудовий досвід вперше був виконаний Бенаром на початку нашого століття, а самі осередки отримали назву осередків Бенара.
Елементарне якісне пояснення причини руху рідини полягає в наступному . Із-за теплового розширення рідина розшаровується, і в більш нижньому шарі щільність рідини r1 менше, ніж у верхньому r2 . Виникає інверсний градієнт щільності, направлений протилежно силі тяжіння . Якщо виділити елементарний об'єм V, який трохи зміщується вгору в наслідку обурення, то в сусідньому шарі архімедова сила стане більше сили тяжіння, оскільки r2 > r1 . У верхній частині малий об'єм, зміщуючись вниз, потрапляє в область зниженої щільності, і архімедова сила буде менше сили тяжіння FA < FT, виникає низхідний рух рідини. Напрям руху низхідного і висхідного потоків в даному осередку випадково, рух же потоків в сусідніх осередках, після вибору напрямів в даному осередку детерміновано. Повний потік ентропії через межі системи негативний, тобто система віддає ентропію, причому в стаціонарному стані віддає стільки, скільки ентропії проводиться усередині системи (за рахунок втрат на тертя).
dSe q q T1 - T2
¾ = ¾ - = q * ¾¾¾ < 0 (3.1)*¾¾¾
dt T2 T1 T1 * T2
Освіта саме стільникової комірчастої структури пояснюється мінімальними витратами енергії в системі на створення саме такої форми просторової структури . При цьому в центральній частині осередку рідина рухається вгору, а на її периферії - вниз.
Подальше надкритичне нагрівання рідини приводить до руйнування просторової структури - виникає хаотичний турбулентний режим.
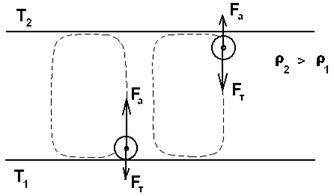
Мал. 3.2. Ілюстрація виникнення теплової
конвекції в рідині .
3.2 ЛАЗЕР, ЯК СИСТЕМА, ЩО САМООРГАНИЗУЄТЬСЯ
У другому розділі це питання ми вже розглядали . Тут же, розглянемо просту модель лазера.
Лазер - це пристрій, в якому в процесі випромінювання, що стимулює, породжуються фотони.
Зміна з часом числа фотонів n, або іншими словами, швидкість породження фотонів, визначається рівнянням вигляду :
dn / dt = «Приріст» - «Втрати» (3.2)
Приріст обумовлений так званим що стимулює випромінюванням . Він пропорційний числу вже наявних фотонів і числу збуджених атомів N . Таким чином :
Приріст = G N n (3.3)
Тут G - коефіцієнт посилення, який може бути отриманий з мікроскопічної теорії . Член, що описує втрати, обумовлений відходом фотонів через торці лазера . Єдине допущення, яке ми приймаємо, - це те, що швидкість відходу пропорційна числу наявних фотонів. Отже
Втрати = 2nc (3.4)c
2c = 1/ t0, де t0 - час життя фотона в лазері .
Тепер слід врахувати одну важливу обставину, яка робить (2.1) нелінійним рівнянням вигляду :
![]() (3.5)
(3.5)
Число збуджених атомів зменшується за рахунок випускання фотонів . Це зменшення DN пропорційно числу наявних в лазері фотонів, оскільки ці фотони постійно примушують атоми повертатися в основний стан .
DN = an (3.6)a
Таким чином, число збуджених атомів рівне
N = N0 - DN (3.7)D
де N0 - число збуджених атомів, підтримуване зовнішньою
накачуванням, у відсутності лазерної генерації.
Підставляючи (3.3) - (3.7) в (3.2), отримуємо основне рівняння наший спрощеній лазерній моделі :
![]() (3.8)
(3.8)
де постійна до дає вираз :
k1 = aG
до = 2 c- GN0 >< 0 (3.9)
Якщо число збуджених атомів N0 (створюваних накачуванням) невелике, то до позитивно, тоді як при достатньо великих N0 до - може стати негативним . Зміна знаку відбувається коли
GN0 = 2c (3.10)c
Ця умова є умова порогу лазерної генерації .
З теорії біфуркації виходить, що при до > 0 лазерної генерації немає, тоді як при до < 0 лазер випускає фотони.
Нижче або вище за поріг лазер працює в здійснено різних режимах .
Вирішимо рівняння (3.8) і проаналізуємо його аналітично :
- це рівняння одномодового лазера .
Запишемо рівняння (3.8) в наступному вигляді :
![]()
Розділимо початкове рівняння на n2 .
![]()
і введемо нову функцію Z :
1/n = n-1 = Z Þ Z1 = - n-2 отже рівняння прийме вигляд :
![]()
перепишемо його в наступному вигляді :
![]()
розділимо обидві частини даного рівняння на -1, отримаємо
![]() (3.11)
(3.11)
Рівняння (3.11) - це рівняння Бернуллі, тому зробимо наступну заміну
Z = UV×, де U і V невідомі поки функції n, тоді Z1 = U1 V + U V1 .
Рівняння (3.11), після заміни змінних, приймає вигляд
U1 V + UV1 - до UV = k1
перетворимо, отримаємо
U1 V + U(V1 - до V)= k1 (3.12)
Вирішимо рівняння (3.12)
V1 - до V = 0 ® dV/dt = до V
зробимо розділення змінних
dV/V =k dt ® ln V = до t
результат V = ekt (3.13)
Звідси ми можемо рівняння (3.12) переписати у вигляді :
U1 ekt= k1- це те ж саме, що dU/dt = k1e-kt, dU = k1e -ktdt виразимо звідси U, отримаємо
![]() (3.14)
(3.14)
По рівнянню Бернуллі ми робили заміну Z = U V підставляючи рівняння (3.13) і (3.14) в цю заміну, отримаємо
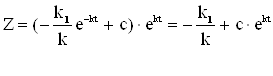
Раніше вводили функцію Z = n-1, отже
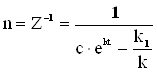 (3.15)
(3.15)
Початкова умова n0=1/(c-k1/k), з цієї умови ми можемо визначити константу з наступним чином

Підставляючи, знайдену нами константу в рівняння (3.15), отримаємо
 (3.16)
(3.16)
Досліджуємо функцію (3.16) при до = 0, до < 0, до > 0 .
При k0 ®; ekt ® 0 ; (ekt - 1)®0, тобто (ekt - 1)×k1/k0®×¥ (невизначеність), розкриємо цю невизначеність за правилом Лопіталя . Цю невизначеність вигляду 0¥ слід привести до вигляду ![]() . При цьому, як і завжди при застосуванні правила Лопіталя, по ходу обчислень рекомендується спрощувати вирази, що вийшли, таким чином :
. При цьому, як і завжди при застосуванні правила Лопіталя, по ходу обчислень рекомендується спрощувати вирази, що вийшли, таким чином :
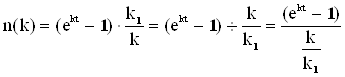
n(k)при k0®® 0, отже 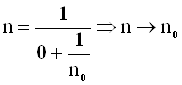
Перепишемо (3.16) в наступному вигляді
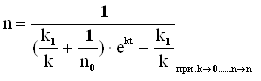
Лінеарізуєм нелінійне рівняння, отримаємо
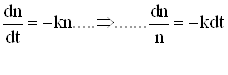
![]() ln n = - kt + з Þ
ln n = - kt + з Þ ![]()
Побудуємо графік для цих умов
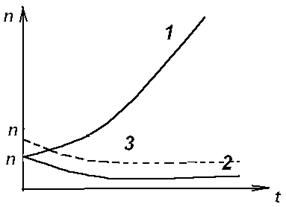
Мал. 3.3 До самоорганізації в одномодовому лазері :
крива 1 : до < 0, режим лазерної генерації
крива 2 : до = 0, точка біфуркації, поріг
крива 3 : до > 0, режим лампи.
При до = 0 рівняння (3.8) прийме вигляд
![]()
вирішуючи його, отримаємо

![]() (3.8)
(3.8)
За умови ![]() ; n(t)= const, функція (3.8) наближається до стаціонарного стану, не залежно від початкового значення n0, але залежно від знаків до і k1 (дивися малюнок 3.3).
; n(t)= const, функція (3.8) наближається до стаціонарного стану, не залежно від початкового значення n0, але залежно від знаків до і k1 (дивися малюнок 3.3).
Таким чином, функція (3.8) ухвалює стаціонарне рішення
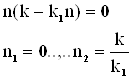
Похожие работы
... а потім дві незалежні частоти. Хаотичний режим, що характеризується суцільним спектром, з'являвся відразу слідом за квазіперіодичною двохчастотною течією. Розділ 5. Застосування понять фізики відкритих систем до моделювання обробки інформації. Знання основних закономірностей утворення структур в активних середовищах, а також у мережах, що складаються з великої кількості активних елементів, ...
... это то, что устраняет неопределенность, количество "снятой" неопределенности. Тенденция к определенности, к повышению информативности - процесс негэнтропийный (процесс с обратным знаком). Термин "самоорганизующаяся система" ввел кибернетик У. Росс Эшби для описания кибернетических систем. Для самоорганизующихся систем характерны: 1) Способность активно взаимодействовать со средой, изменять ...
... проблемы, где соответствующей проверки не производилось. При обнаружении расхождений так создаваемых концепций с реально наблюдаемыми явлениями неизбежно возникало недоумение, граничащее с попытками отрицания самой возможности познания окружающего мира. Современное естествознание характеризуется лавинообразным накоплением нового фактического материала и возникновением множества новых дисциплин ...
... субъекта (Юм), априорным формам мышления (Кант), целевым установкам личности (прагматизм), интерсубъективным конвенциям (А. Пуанкаре) и др. Фундаментальными проблемами в данной сфере выступали в классической философии проблема критерия И., трактовка которого соответствовала принятому определению И. (от эйдотического образца у Платона до Божественной Мудрости у Фомы Аквинского, с одной стороны, и ...
0 комментариев