Проводимость четверти цилиндра (проводимость между ребром АВ торца полюса и плоскостью, рис. 2.5, а)

1. Проводимость четверти цилиндра (проводимость между ребром АВ торца полюса и плоскостью, рис. 2.5, а)

 

; . (2.13).

Проводимость для полюс — полюс (проводимость полуцилиндра, рис.2.5, б

(2.14)

2. Проводимость четверти полого цилиндра (проводимость между боковой гранью полюса и плоскостью, рис. 2.5, в)

 

(2.15)

где удельные проводимости  определяются по кривым Ротерса соответственно из рис. 2.3 и рис. 2.4.

3. Проводимость половины сферического квадранта (проводи
мость между углом А полюса и плоскостью, рис. 2.5, г):

(2.16)

4.Проводимость половины квадранта сферической оболочки
(проводимость между боковым ребром А В полюса и плоскостью,

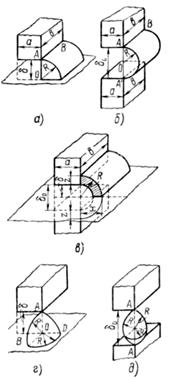Рис. 2.5. К определению магнитной проводимости поля с ребра, угла и боковой поверхности полюса

Для полюс — полюс (проводимость между боковыми ребрами АВ и А'В', рис2.6, б):

(2.17)

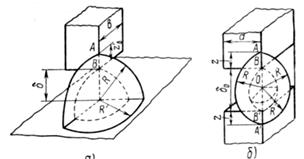
Рис. 2.6. К расчету магнитной проводимости поля с ребра боковых граней

 

Расчет магнитных проводимостей воздушных путей графическим методом

Для практических целей широко используются магнитные цепи, у которых магнитная проводимость рассеяния на единицу длины сердечника непостоянна. Поле таких цепей неоднородно. Оно сильно зависит от формы магнитопровода, расположения катушки и величины м. д. с, и поэтому точный расчет трехмерных реальных цепей невозможен. Известные в литературе формулы проводимостей получены при упрощении истинной картины поля и, кроме того, определяются только для отдельных участков магнитной цепи. Разработка приближенной, но достаточно простой, методики расчета, пригодной для любых конструктивных форм и удовлетворяющей требованиям точности, является практически важной задачей.

Исследования показали, что эту задачу можно решить приближенно, сочетая графический метод с аналитическим. Графический метод Лемана — Рихтера успешно применяется при расчете поля электрических машин, так как он сравнительно прост и дает вполне удовлетворительные результаты. Однако попытка применить его к расчету магнитных систем электрических аппаратов встретила определенные трудности.

Если в электрических машинах размеры магнитной системы в осевом направлении велики и поле можно считать плоскопараллельным, то в магнитных системах аппаратов все размеры соизмеримы, поэтому поле является трехмерным. Кроме того, поле многих аппаратов еще усложняется наличием ряда воздушных зазоров и обмоток возбуждения, Методика расчета, изложенная ниже, учитывает эти особенности и охватывает цепи с распределенной и сосредоточенной м. д. с.

Исследования показали, что форма поля при прочих равных условиях зависит от расположения намагничивающей катушки на магнитопроводе и от соотношения 1/с

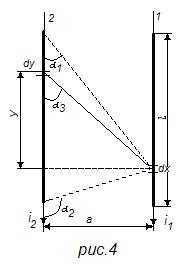
Построить объемное поле даже для простейшей магнитной цепи не представляется возможным, но с достаточной для практики точностью оно может быть представлено в виде суммы частичных объемных полей, где в пространстве, например между гранями полюсов1 и 2 в направлении грани в поле принимается плоскопараллельным, а в остальной части пространства объемное поле подсчитывается по приближенным формулам.

Определение магнитной проводимости воздушного зазора при постоянном магнитном напряжении между ферромагнитными поверхностями

Участок любого плоско параллельного магнитного поля можно характеризовать совокупностью линии напряженности поля и линий ровного магнитного потенциала.

При построении картины поля должны выполняться следующие условия:

1. магнитное сопротивление стали ферромагнитного тела полюсов и сердечников принимается равным нулю, вследствие чего линии индукции нормальны к поверхности ферромагнитных тел, которые в свою очередь являются поверхностями равного магнитного потенциала;

2.  на всех участках поля линии напряженности поля (сплошные) и линии равного магнитного потенциала (пунктирные) должны пересекаться под прямыми углами (рис. 4.30, а);

3.  средняя длина l_ср и средняя ширина b_ср единичной трубки берутся приближенно равными.

В общем случае полная проводимость какого-либо участка магнитного поля может быть определена формулой

(2.17)

где удельная магнитная проводимость участка

(2.17)

ΔU

Ф — магнитный поток рассматриваемого участка поля; ΔФ — поток в одной трубке;

U — магнитное напряжение, приложенное между рассматриваемой длиной участка;

ΔU— магнитное напряжение, приложенное к единичной трубке; т — число элементарных трубок потока в рассматриваемом участке;

п — число единичных трубок, последовательно соединенных в элементарной трубке;

ΔG— проводимость единичной трубки на глубине поля в.

Лекция № 3

Тема лекции:

Расчет магнитной цепи электромагнитов постоянного тока, обмоточных данных. Магнитные цепи электромагнитов переменного тока. Расчет обмоток

ЭЛЕКТРОМАГНИТЫ

 

Общие сведения о магнитных цепях аппаратов

а) Магнитная цепь аппарата, основные законы. Электромагниты нашли в аппаратостроении широкое применение и как элемент привода аппаратов (контакторы, пускатели, реле, автоматы, выключатели) и как устройство, создающее силы в муфтах, тормозах и подъемных механизмах.

Конфигурация магнитной цепи электромагнита зависит от назначения аппарата и может быть самой разнообразной.

Основные соотношения для магнитной цепи мы рассмотрим на примере клапанной системы, изображенной на рис. 3.1. Подвижная часть магнитной цепи называется якорем 1. Часть магнитной цепи, на которой сидит намагничивающая катушка 2, называется сердечником 3. Вертикальные и параллельные части магнитопровода 3 и 4 часто называют стержнями.

В клапанной системе якорь может иметь как поступательное движение так и вращательное.

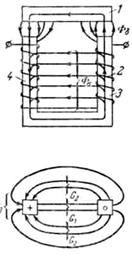
Рис. 3.1. Магнитная цепь клапанной системы

Намагничивающая катушка создает намагничивающую силу (н. с), под действием которой возбуждается магнитный поток. Этот поток замыкается как через зазор б, так и между другими частями магнитной цепи, имеющими различные магнитные потенциалы.

Воздушный зазор б, меняющийся при перемещении якоря, называется рабочим зазором. Соответственно поток, проходящий через рабочий зазор, называется рабочим потоком и обозначается обычно Ф₅. Все остальные потоки в магнитной цепи называются потоками рассеяния Ф_в. Сила, развиваемая якорем электромагнита, как правило, определяется потоком в рабочем зазоре Ф_ъ.

Задачей расчета магнитной цепи является либо определение н. с. катушки, необходимой для создания рабочего потока заданной величины (прямая задача), либо определение рабочего потока по известной н. с. катушки (обратная задача). Эти задачи могут быть решены с помощью двух законов Кирхгофа применительно к магнитной цепи.

Согласно первому закону алгебраическая сумма потоков в узле магнитной цепи равна нулю:

(3.1)

Второй закон Кирхгофа можно получить из известного закона полного тока H

(3.2)

где Н — напряженность магнитного поля;

dl— элемент длины, по которому проходит магнитный поток;

 — сумма н. с., действующих в контуре.

Помня, что , можно написать в виде

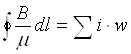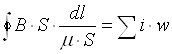 ,  (3.3)

S

d l/χ

где S — сечение магнитной цепи; µ— магнитная проницаемость.

Магнитная проницаемость µ характеризует проводимость магнитного материала цепи. Выражение d l/µS аналогично сопротивлению элемента электрической цепи dl/xS (где χ — электрическая проводимость материала проводника). Тогда можно представить в виде

(3.4)

где dR dRS — магнитное сопротивление участка длиной- dl.

Падение магнитного потенциала по замкнутому контуру равно сумме намагничивающих сил, действующих в этом контуре. Это и есть второй закон Кирхгофа магнитной цепи.

В системе единиц СИ размерность, следовательно, магнитное сопротивление получает размерность — единица, деленная на генри.

В том случае, когда поток в отдельных частях магнитной цепи не меняется, интеграл можно заменить конечной суммой

(3.5)

Таким образом, сумма падений магнитного напряжения по замкнутому контуру равна сумме намагничивающих сил, связанных с потоками, проходящими через магнитную цепь.

По аналогии с электрической цепью магнитное сопротивление участка конечной длины l можно представить в виде

(3.6)

где ρµ —магнитное сопротивление единицы длины магнитной цепи при сечении, также равном единице, м/гн.

Полная аналогия законов Кирхгофа электрической и магнитной цепей позволяет составить для последней электрическую схему замещения.

Для расчета по (3.5) необходимо иметь кривую ρµ(B). Если задана не кривая ρµ(B), а кривая намагничивания материала B(H), для расчета удобно использовать (3.2). Если на отдельных участках индукция постоянна, то интеграл в (3.2) можно заменить конечной суммой

(3.7)

По известной индукции в каждом участке с помощью кривой В(Н) находят напряженность Hj на участке, после чего с помощью (3.7) можно отыскать потребную н. с. катушки.

При расчете магнитной цепи часто более удобным является введение величины, обратной магнитному сопротивлению — магнитной проводимости

(3.8)

Уравнение (3.5) при этом принимает вид:

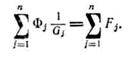
(3.9)

Для простейшей неразветвленной цепи

(3.10)

Магнитное сопротивление и проводимость ферромагнитных материалов являются сложной нелинейной функцией индукции. Зависимость относительной магнитной проницаемости , а следовательно, и магнитной проводимости от величины индукции для магнитномягкого материала представлена на рис.1.2. Максимальное значение  (минимальное магнитное сопротивление) имеет место при средних величинах индукции. В слабых и сильных полях магнитное сопротивление материала резко возрастает. Изменение магнитного сопротивления от величины индукции сильно затрудняет решение как прямой, так и обратной задачи.

Магнитная цепь электромагнитов постоянного тока

а.) Расчет потоков рассеивания и индуктивности катушки без учета сопротивления стали. Для электромагнитов, у которых катушка располагается на стержне, поток рассеяния связан с катушкой так, что с различными витками сцеплен различный поток рассеяния. Такая система называется системой с распределенной намагничивающей силой.

Рассмотрим закон изменения потока вдоль сердечников и разности магнитных потенциалов между ними в клапанной системе (рис. 3.1).

Намагничивающая сила на единицу длины стержня равна Iw/l. Разность магнитных потенциалов между точками, расположенными на расстоянии х от основания, равна . Тогда элементарный поток рассеяния с участка dx, расположенного на расстоянии х от основания, можно найти с помощью

 (3.12)

Произведя интегрирование в пределах от 0 до х, получим поток, выходящий из стержня на длине х

(3.13)

Поток, проходящий через сечение сердечника на расстоянии х от основания, равен:

(3.14)

поток в основании сердечника получим, положив х = 0:

(3.15)

Без учета сопротивления магнитопровода

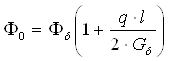  . (3.16)

Разность магнитных потенциалов между стержнями меняется по линейному закону и достигает максимального значения Iw у рабочего воздушного зазора. Магнитный поток согласно (3.14) меняется по закону параболы и достигает максимального значения у основания стержня. Известно, что индуктивность катушки L, от которой в большой степени зависит время срабатывания электромагнита, определяется как отношение потокосцепления ^х¥ к току.

Тогда

(3.17)

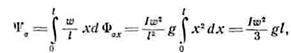
но (3.18)

следовательно,

(3.19)

Магнитная цепь электромагнитов переменного тока

Магнитные цепи на переменном токе обладают следующими особенностями.

1. Ток в катушке электромагнита зависит главным образом от ее индуктивного сопротивления.

2. Магнитное сопротивление цепи зависит от потерь в стали и наличия короткозамкнутых обмоток, расположенных на сердечнике.

3. Магнитопровод обычно выполняется шихтованным (с целью уменьшения потерь на вихревые токи) прямоугольного поперечного сечения.

а) Магнитная система без активных потерь в стали и насыщения. Ради упрощения при расчете магнитной пени мы сделаем допущения, что напряжение, ток в катушке и потоки меняются по синусоидальному закону.

Рассмотрим вначале простейшую цепь без учета сопротивления стали, потерь в ней и потоков рассеяния. Напряжение сети, приложенное к катушке, уравновешивается активным и реактивным падением напряжения

(3.20)

где напряжение U и ток / берутся в действующих значениях.

Воспользовавшись (5-12) и (5-8), получим:

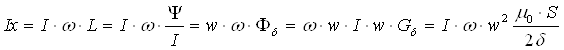
(3.21)

Для случая шунтовой обмотки, когда катушка подключается на зажимы источника напряжения, активное сопротивление обмотки, как правило, значительно меньше реактивного . Если пренебречь активным падением напряжения, то U=IX. Но так как

(3.22)

получим

(3.23)

где Ф_т — амплитудное значение потока.

Таким образом, при сделанных выше допущениях (активное сопротивление обмотки и потери в сердечнике равны нулю) поток, связанный с катушкой, не зависит от рабочего зазора и является величиной постоянной.

При допущении, что U=IX, из (3.21) следует

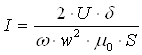 (3.24)

С ростом зазора индуктивное сопротивление обмотки уменьшается, а ток в обмотке увеличивается в соответствии (3.24); поскольку величина потока согласно (3.23) должна остаться неизменной, то соответственно с ростом зазора б растет н. с. Iw, т. е. ток. Если учесть активное сопротивление обмотки (при условии, что в заданном диапазоне изменения зазора R<^.(oL), то с ростом зазора величина тока будет расти, а величина потока будет уменьшаться согласно уравнению

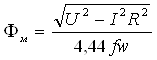 (3.25)

Rδ

Таким образом, с ростом рабочего зазора величина потока будет падать с зазором, как это имеет место и в цепи постоянного тока. Однако в магнитной цепи переменного тока уменьшение потока является следствием роста падения напряжения на активном сопротивлении обмотки, а в цепи постоянного тока — роста магнитного сопротивления воздушного зазора.

Если учитывать поток рассеяния Фδ то в схеме замещения параллельно сопротивлению R_b, зависящему от величины зазора, необходимо включить неизменное сопротивление R_a. В результате при увеличении зазора ток в обмотке нарастает меньше, чем это следует из (3.24).

При составлении электрической схемы замещения магнитной цепи магнитное сопротивление воздушных промежутков ^2 = ^ = ^ заменяется численно равным ему активным сопротивлением.

В электрических аппаратах, работающих на переменном токе, для изменения фазы магнитного потока применяются короткозамкнутые витки и обмотки. Влияние последних может быть учтено введением в схему замещения реактивного (индуктивного) сопротивления

Действительно, пусть в клапанной системе рис. потери в магнитопроводе и его магнитное сопротивление равны нулю, а ключ А включен. Магнитный поток, проходя через контур витка w_K, наводит в нем э. д. с. Возникающий в витке ток создает свой магнитный поток. Ради упрощения рассуждений положим, что Х_к = 0. Для мгновенного значения н. с. обмотки можно написать:

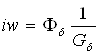
  (3.26)

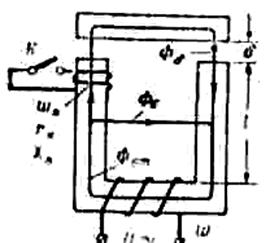
Рис. 3.2.Магнитая цепь с к. з. обмоткой

Используя полученные соотношения, получаем:

(3.27)

Для электрической цепи, состоящей из последовательно включенного сопротивления и индуктивности, падение напряжения может быть выражено:

(3.28)

Проводя аналогию между магнитной и электрической цепью, введем понятие реактивного магнитного сопротивления.

Мгновенному значению тока i соответствует мгновенное значение потока Фδ; активному сопротивлению цепи R —активное —магнитное сопротивление Rµ, индуктивности L — величина . Для электрической цепи переменного тока в комплексной форме можно записать:

(3.29)

где

Аналогично для магнитной цепи

(3.30)

где

Таким образом, короткозамкнутая обмотка с чисто активным сопротивлением в схеме замещения представляется реактивным магнитным сопротивлением. Если Л;=°° (т. е. обмотка разомкнута), то X =0. Если г_к = 0, то X =оо и магнитный поток через такую обмотку пройти не может. Если обмотка имеет и активное г_к и индуктивное Х_к сопротивление, то согласно.

(3.31)

б) Магнитная цепь с потерями в стали. При протекании потока по магнитопроводу в нем создаются активные потери за счет вихревых токов и гистерезиса. Эти потери в схеме замещения магнитной цепи могут быть представлены потерями в фиктивной короткозамкнутой обмотке, имеющей только активное сопротивление. Параметры этой обмотки находятся из условия равенства потерь в стали и потерь в этой короткозамкнутой обмотке.

При синусоидальном изменении потока

(3.32)

откуда

Из условия равенства потерь можно записать:

(3.33)

Воспользовавшись полученными соотношениями можно получить:

(3.34)

Таким образом, зная активные потерн в стали и магнитный поток в сечении, можно определить Хщ._г, учитывающее в схеме замещения потери на вихревые токи и гистерезис.

Кроме реактивного магнитного сопротивления, сталь обладает также активным магнитным сопротивлением R

Аналогично электрической цепи можно ввести понятие удельного активного магнитного сопротивления

где р_д — удельное активное магнитное сопротивление стали;

(3.35)

где Р₀— потери на единицу массы сердечника; у — плотность; l и S — длина и сечение сердечника; р_л-— удельное реактивное магнитное сопротивление стали;

(3.36)

где p_z — полное удельное магнитное сопротивление стали.

Зависимость р_л, p^_Y и pz от индукции для стали Э-12 представлена на рис. Так как

(3.37)

Если задан поток Ф,„ и известны размеры участка •S и /, то сначала находят индукцию B_m = (&_m/S, а затем по кривым, аналогичным рис.3.3, определяют р_л, р*, Pz. Воспользовавшись (3.35), (3.36)и (3.37) можно вычислить магнитные сопротивления У? , X и %

Однако чаще дается кривая намагничивания на переменном токе, связывающая максимальное значение индукции В_т с действующим значением напряженности Н с учетом активных потерь.

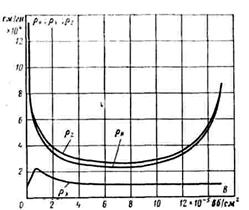
Рис.3.3 Удельные сопротивления стали.

(3.38)

Расчет магнитной цепи переменного тока ведется с помощью двух уравнений Кирхгофа в комплексной форме методом последовательных приближений.

Если задано напряжение на обмотке, ее активное сопротивление и размеры магнитной цепи, то сначала находят поток без учета сопротивления стали и активного сопротивления катушки из, а затем строят схемы замещения, уточняя каждый раз значения магнитных сопротивлений, потоков и н. с. Расчет производится до тех пор, пока потоки в рабочем зазоре двух соседних приближений будут отличаться друг от друга не более чем на 10%.

 

Катушки электромагнитов

В результате расчета магнитной цепи определяется поток в катушке и ее н. с. Катушка должна быть рассчитана таким образом, чтобы, с одной стороны, обеспечить требуемую н. с, а с другой — чтобы максимальная температура обмотки не превышала допустимой для используемого класса изоляции.

В зависимости от способа включения различают параллельные (шунтовые) и последовательные (сериесные) обмотки. В первом случае напряжение, приложенное к обмотке, постоянно по своему действующему значению.

Во втором — сопротивление обмотки электромагнита во много раз меньше сопротивления остальной части цепи.

а) Расчет обмотки электромагнита постоянного тока. Эскиз обмотки представлен на рис.. Заданы напряжение U и н. с. Iw. Требуется рассчитать и спроектировать катушку. Сечение провода q находим, исходя из потребной н. с.

 

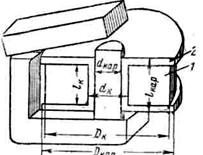
Рис.3.4Электромагнит с обмоткой.

(3.39)

или

где р —удельное сопротивление; /_ср —средняя длина витка; R — сопротивление обмотки

Из уравнения следует, что при неизменной средней длине витка и заданном р н. с. определяется произведением Uq. Если при неизменном напряжении и средней длине витка требуется увеличить н. с, то необходимо взять провод большего сечения. При этом обмотка будет иметь меньшее число витков.

После определения сечения провода с помощью таблиц сортаментов находится ближайший стандартный диаметр провода.

Если выполнить обмотку проводом данного диаметра, то н. с. обмотки не будет зависеть от способа укладки провода. При «дикой» (нерядовой) обмотке число витков при том же окне уменьшится по сравнению с рядовой, величина тока пропорционально увеличится, а н. с. катушки останется без изменения.

Мощность, потребляемая катушкой, при дикой обмотке увеличится, поскольку уменьшится коэффициент

При изменении питающего напряжения и сохранении размера окна обмотки должно иметь место равенство так каки  остаются неизменны. При этом  н. с. обмотки останется без изменения. Поскольку при переходе с одного напряжения на другое изменяется диаметр провода (а следовательно, и толщина изоляции), коэффициент заполнения обмотки также меняется. Можно получить:

Еслито при переходе с напряжения и_{ на

£/₂ диаметр провода уменьшится. При меньшем диаметре провода из-за возросшей относительной толщины изоляции коэффициент заполнения уменьшится. Следовательно, при переходе на более высокое напряжение мощность, потребляемая катушкой, увеличивается.

Для ориентировочной оценки нагрева катушки можно пользоваться следующими рекомендациями. Опытным путем установлено, что в катушке на изоляционном каркасе, выполненной проводом ПЭЛ, максимальная температура не превысит 105°С, если на каждый ватт выделяемой мощности будет приходиться определенная боковая поверхность (ао=5б„,,/Я — удельная охлаждающая боковая поверхность). Величина этой поверхности зависит от геометрии катушки:

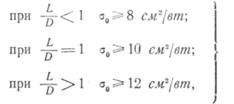
(3.40)

гдедлина катушки;внешний диаметр.

Если после расчета окажется, чтото это значит, что температура обмотки будет выше допустимой.

Можно получить:

(3.41)

Если при требуемой н. с. мощность Р получается больше, чемто либо необходимо уменьшить н. с. обмотки, либо увеличить площадь обмоточного окна Q_K.

После приближенной оценки теплового режима катушки необходимо определить максимальную температуру внутри ее.

Для последовательной обмотки исходными величинами для расчета являются н. с. {Iw) и ток цепи /„. Число витков обмотки находится из выражения

(3.42)

Сечение провода можно выбрать исходя из рекомендуемой плотности тока, равной 2—4 а/мм² — для продолжительного режима работы, 5—12 а/мм² — для повторно-кратковременного режима работы, 13—30 а/мм²— для кратковременного режима работы. Эти величины можно увеличить примерно в 2 раза при сроке службы до 500 ч.

Окно, занимаемое рядовой обмоткой, определяется числом витков и диаметром провода по изоляции.

б) Расчет обмотки электромагнитов переменного тока. Исходными данными для расчета параллельной катушки являются амплитуда н. с, амплитуда потока и напряжение. Напряжение сети уравновешивается активным и реактивным падением напряжения

(3.43)

Поскольку величины тока и сопротивления могут быть рассчитаны только после определения числа витков, то представленное выражение не позволяет сразу найти все параметры катушки. Задача решается методом последовательных приближений.

Так как активное падение напряжения значительно меньше неактивного, то в начале расчета можно положитьТогда число витков обмотки равно:

Так как при расчете w мы пренебрегаем активным падением напряжения, действительное число витков должно быть несколько меньше. Обычно берут

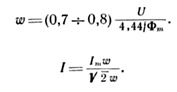
(3.44)

Сечение провода обмотки определяют, задавшись плотностью тока. Выбрав стандартный диаметр и способ укладки, находим коэффициент заполнения /_м и площадь окна катушки и:

(3.45)

После этого определяем среднюю длину витка и активное сопротивление обмотки

(3.46)

Теперь производим проверку выбранных параметров: если напряжение сети в квадрате U² отличается от суммы (IR)² и (4,44шф_т)² более чем на 10%, то необходимо варьировать число витков до тех пор, пока не получим удовлетворительного совпадения.

После расчета активного сопротивления производится проверка катушки на нагрев. Расчет ведется так же, как и для катушек постоянного тока. Характерной особенностью здесь является нагрев магнитопровода за счет потерь от вихревых токов и гистерезиса. Отвод тепла, выделяемого в самой катушке через сердечник, затруднен. Поэтому точка с максимальной температурой лежит на внутреннем радиусе катушки. Из-за плохого охлаждения катушки через сердечник в катушке стремятся развивать поверхность торцов, через которые может отдаваться значительная часть тепла.

Если полное сопротивление обмотки электромагнита при любом рабочем зазоре значительно меньше полного сопротивления цепи (последовательная обмотка), то величина тока в обмотке электромагнита не зависит от положения якоря. Расчет таких обмоток ведется так же, как и для последовательных обмоток постоянного тока. Закон изменения потока в рабочем зазоре такого электромагнита аналогичен закону в электромагните постоянного тока, поскольку электромагнит работает при постоянной н. с. катушки.

Полное падение напряжения на обмотке электромагнита равно:

(3.47)

Если электромагнит с параллельной катушкой питается от источника с другим напряжением и сила тяги должна остаться той же, то обмоточные данные должны быть соответственно изменены. Величина н. с. и угол сдвига между током и напряжением при этом также считаются неизменными. Должны быть соблюдены следующие соотношения:

(3.48)

Полная мощность обмоток при переходе с одного напряжения на другое при соблюдении указанных условий не изменяется, так как

(3.49)

Магнитные материалы для электромагнитов постоянного и переменного тока

При заданном потоке падение магнитного потенциала уменьшается с уменьшением магнитного сопротивления. Так как сопротивление обратно пропорционально магнитной проницаемости материала, при данном потоке магнитная проницаемость должна быть возможно выше. Это позволяет уменьшить н. с. катушки и мощность, необходимую для срабатывания электромагнита; уменьшаются размеры катушки, обмоточного окна и всего электромагнита. Уменьшение н. с. катушки при прочих неизменных параметрах уменьшает температуру обмотки.

Вторым важным параметром материала является индукция насыщения. Сила, развиваемая электромагнитом, пропорциональна квадрату индукции. Поэтому чем больше величина допустимой индукции, тем больше величина развиваемой силы при тех же размерах.

После того как катушка электромагнита обесточивается, в системе существует остаточный поток, который определяется коэрцитивной силой материала и проводимостью рабочего зазора. Остаточный поток может привести к залипанию якоря. Во избежание этого явления требуется, чтобы материал обладал низкой коэрцитивной силой (малой шириной петли гистерезиса).

Существенными требованиями являются низкая стоимость материала и его технологичность.

В электромагнитах переменного тока для компенсации активных потерь в стали приходится затрачивать дополнительную энергию. Это приводит к увеличению намагничивающего тока в катушке аппарата. В связи с этим материалы, используемые для электромагнитов переменного тока, должны иметь малые потери на вихревые токи и гистерезис. Сердечники для таких электромагнитов делаются шихтованными, причем чем выше частота тока, тем меньше должна быть толщина листа. Пластины магнитопровода изготавливаются из листовой стали штамповкой. Для быстродействующих электромагнитов постоянного тока также применяются шихтованные сердечники, так как при этом уменьшаются вихревые токи, дающие замедление нарастания потока.

Наряду с указанными свойствами магнитные характеристики материалов должны быть стабильны (не меняться от температуры, времени, механических ударов).

Лекция №4

Тема лекции:

Энергетический баланс электромагнита постоянного тока. Расчет силы тяги, формула Максвелла. Сила тяги электромагнитов переменного тока. Магнитный демпфер

СИЛА ТЯГИ ЭЛЕКТРОМАГНИТОВ

а) Энергетический баланс электромагнита постоянного тока. Рассмотрим процесс возникновения магнитного поля в простейшем клапанном электромагните (рис. 4.1,а). После включения цепи напряжение источника уравновешивается активным падением напряжения и э. д. с. самоиндукции:

(4.1)

Умножив обе части уравнения на idt, получим:

(4.2)

Произведя интегрирование, получим:

 

(4.3)

где потокосцепление к моменту времени

Левая часть равенства представляет энергию, которая затрачена источником тока. Первый член правой части есть потери энергии в активном сопротивлении цепи, второй—энергия, затраченная на создание магнитного поля. До тех пор, пока сила, развиваемая электромагнитом, меньше силы пружины, якорь электромагнита неподвижен, и потокосцепление нарастало при неизменном значении рабочего зазора^А- Зависимость  при этом зазоре представлена кривой 1 рис..

Допустим, что при достижении значения потокосцепления Wt сила электромагнита стала больше силы пружины и якорь переместился в положение, при котором рабочий зазор стал равен Так как при меньшем зазоре проводимость рабочего зазора возрастает, потокосцепление увеличится до значения _ Величина тока при этом увеличится до значения' Если изобразить зависимость при зазорето получим кривую 2 рис.4.1б. До начала трогания якоря энергия магнитного поля, запасенная в цепи, равна:

(4.4)

где масштаб по оси тока, А/мм; масштаб  по оси потокосцепления, площадь криволинейного треугольника Оаb, мм

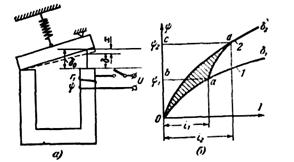
Рис.4.1 К определению силы тяги электромагнита

При движении якоря потокосцепление изменится от  до Энергия магнитного поля при этом возросла на величину .4₂, равную:

(4.5)

гдеплощадь криволинейной трапеции.

При переходе от зазорак зазору_ якорь электромагнита совершил механическую работу Л₃.

Энергия, накопленная в магнитом поле, к концу хода равна Л₄:

(4.6)

На основании закона сохранения энергии можно написать:

(4.7)

Механическая работа, совершенная якорем электромагнита, определяется из

(4.8)

Согласно рис. эта энергия равна:

(4.9)

б) Расчет силы тяги электромагнита постоянного тока. Средняя сила на ходе якоря от 6i до 6₂ равна:

(4.10)

гдеперемещение якоря, а уменьшение зазора.

Следует учитывать, что(рис. 4.1,а). Тогда

Для расчета силы, развиваемой электромагнитом, необходимо определить механическую работу Л₃, совершаемую электромагнитом при небольшом перемещении якоря, после чего разделить эту работу на изменение зазора, что в пределе дает:

(4.11)

Силадействует в сторону уменьшения зазора.

Очевидно, что для каждого элементарного перемещения якоря можно определить свое А₃ и найти среднюю силу, развиваемую на данном участке хода якоря.

Зависимость тяговой силы электромагнита от величины рабочего зазора при неизменном значении тока в его обмотке называется статической характеристикой электромагнита. Величина силы может быть найдена с помощью рис. 4.2:

(4.12)

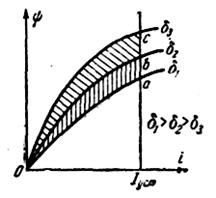
Рис. 4.2. К определению силы тяги

Эта сила развивается электромагнитом при среднем зазоре

(4.13)

Аналогично определяется сила

(4.14)

которая развивается при среднем зазоре

(4.15)

На готовом электромагните статическая характеристика может быть легко снята. Для этого в воздушный зазор электромагнита ставится немагнитная прокладка, после чего к электромагниту подводится напряжение. С помощью динамометра постепенно увеличивается противодействующая сила до тех пор, пока якорь не оторвется от сердечника. Эта сила в момент отрыва будет равна статическому усилию при зазоре, равном толщине прокладки. После этого меняют толщину прокладки и опыт повторяют при новом значении зазора.

Величина силы, развиваемой электромагнитом, может быть рассчитана с помощью формулы Максвелла. Если поле в рабочем зазоре равномерно и полюсы ненасыщены, то формула Максвелла для силы в одном зазоре имеет вид

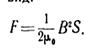
(4.16)

в) Аналитический расчет силы для ненасыщенных электромагнитов. Исходя из закона сохранения энергии, можно показать, что энергия, полученная магнитным полем при элементарном перемещении якоря, равна механической работе, произведенной якорем, и изменению запаса электромагнитной энергии:

(4.17)

гдеэлементарная энергия, полученная полем при перемещении якоря;элементарная работа, произведенная якорем;приращение магнитной энергии.

Из уравнения легко получить:

(4.18)

Учитывая, что (для линейной магнитной цепи), получаем:

(4.19)

Для статической тяговой характеристики так как ток в цепи не меняется. Тогда

 

(4.20)

Для клапанного электромагнита потокосцепление зависит от рабочего потока и потока рассеяния:

(4.21)

Поскольку цепь линейна (пренебрегаем насыщением стали), то потокосцепление обусловленное рабочим потоком Ф_г, равно:

(4.22)

Потокосцепление Ч7_в, обусловленное потоком рассеяния, в свою очередь равно:

(4.23)

Подставив , получим:

(4.24)

Поскольку проводимость рассеяния от зазора б не зависит, тоСила, развиваемая электромагнитом, будет равна:

(4.25)

Если известна аналитическая зависимость, то находится дифференцированием. В уравнение (4.25) подставляется интересующего нас значения зазора  Если G₆ определяется в результате графического построения поля, то вначале производится расчетдля ряда положений якоря, после чего графически строится зависимостьi и производится графическое дифференцирование.

При достаточно малом зазоре для системы рис. 3.1

(4.26)

Тогда величина силы F равна:

(4.27)

Согласно выражению сила, развиваемая электромагнитом, пропорциональна квадрату н. с. катушки, площади полюса и обратно пропорциональна квадрату величины зазора. Зависимость при неизменной н. с. катушки представлена на рис. 4.3 (кривая 1). По мере уменьшения б величина силы резко возрастает, причем при б = 0 сила принимает бесконечное значение. В действительности при б = 0 величина потока в системе определяется магнитным сопротивлением цепи, которое резко возрастает по мере насыщения материала магнитопровода, и сила имеет конечное значение. Кривая 2 на рис.4.3 изображает зависимость , снятую экспериментально. Сравнение этих кривых показывает, что при больших зазорах, когда поток в системе мал и падением магнитного потенциала в сердечнике можно пренебречь, расчетная и экспериментальная кривые почти полностью совпадают. При малых зазорах сила, развиваемая электромагнитом, имеет конечное значение.

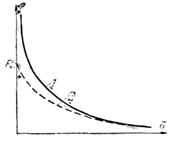
Рис. 4.3. Тяговая характеристика

Многочисленные исследования показали, что для расчета силы в насыщенных электромагнитах можно пользоваться формулой (4.25), но только вместо берется падение магнитного потенциала в рабочем зазоре:

(4.28)

Величину находят в результате расчета магнитных цепей.

Поскольку формула Максвелла учитывает реальную индукцию между полюсами, то она также может быть использована при условии, что поле в зазоре равномерно и вектор индукции перпендикулярен к поверхности полюса.

г) Сила тяги электромагнита переменного тока. Рассмотрим задачу применительно к клапанному электромагниту с двумя рабочими зазорами, сделав следующие допущения: магнитное сопротивление стали, активное сопротивление обмотки и потери в стали равны нулю; напряжение, ток и поток меняются по синусоидальному закону.

В этом случае поток, а следовательно, потокосцепление не зависят от величины зазора .

Тогда мгновенное значение силы будет равно:

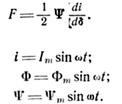
(4.29)

Подставив, получим:

(4.30)

Поскольку  при данном зазорене зависят от времени, можно записать:

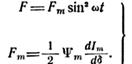
(4.31)

Производная может быть найдена графическим дифференцированием зависимости, которая получается из расчета магнитной цепи. Величина определяется приложенным напряжением.

Мгновенное значение силы при наличии двух рабочих зазоров может быть найдено по формуле Максвелла (4.16). Для амплитуды силы получим:

Поскольку при изменении зазора амплитуда потока и индукции не изменяются, амплитуда силы от зазора не зависит. Однако если учесть активное сопротивление обмотки, то, как было показано, с ростом зазора поток в системе уменьшается, что приводит к уменьшению амплитуды силы.

Рассмотрим теперь изменение силы во времени. Согласно (4.31) сила меняется во времени по следующему закону:

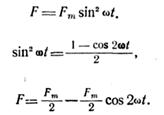
(4.32)

Мгновенное значение силы пульсирует с двойной частотой по отношению к частоте тока. Среднее значение силы равно половине амплитудного значения:

(4.33)

Для притяжения якоря необходимо, чтобы среднее значение силы было больше противодействующего усилия.

Изменение силы во времени отрицательно сказывается на работе электромагнита. В определенные моменты времени сила противодействующей пружины становится больше силы электромагнита, при этом происходит отрыв якоря от сердечника. По мере нарастания силы электромагнита снова происходит притяжение якоря. В результате якорь электромагнита будет непрерывно вибрировать, создавая шум и ненормальные условия работы механизма или контактов. В связи с этим принимаются меры для устранения вибрации.

В однофазных электромагнитах наибольшее распространение получило использование короткозамкнутого витка. Эскиз полюса такого электромагнита представлен на рис.4.4. Наконечник полюса расщеплен, и на большую его часть насажен короткозамкнутый виток, выполненный из меди или алюминия. Для получения более ясной картины примем, что сопротивление стали равно нулю и существует только один рабочий зазор.

Благодаря наличию короткозамкнутого витка поток  отстает по фазе относительно  на угол. Каждый из потоков под своей частью полюса создает свою силу.

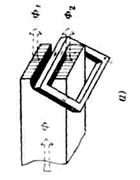
Рис.