Навигация
Электродинамические усилия в электрических аппаратах
Электродинамические усилия в электрических аппаратах
Содержание
1. Основные понятия.............................................................................. 2
Возникновение электродинамических сил........................................................ 2
Направление действия силы.............................................................................. 3
2. Методы расчета электродинамических сил...................................... 4
Первый метод..................................................................................................... 4
Второй метод..................................................................................................... 6
3. Электродинамические силы между параллельными проводниками 8
Бесконечной длины............................................................................................ 8
Конечной длины................................................................................................ 9
Неравной длины.............................................................................................. 10
4. Электродинамические силы между взаимно перпендикулярными проводниками....................................................................................... 15
5. Электродинамические силы в кольцевом витке и между кольцевыми витками............................................................................ 17
Для одного витка............................................................................................. 17
Для нескольких витков.................................................................................... 18
6. Электродинамические силы в проводниках переменного сечения 20
7. Силы взаимодействия между проводником с током и ферромагнитной массой....................................................................... 21
Вблизи ферромагнитной массы...................................................................... 21
Внутри ферромагнитной массы...................................................................... 22
8. Электродинамические силы при переменном токе......................... 24
При однофазном токе...................................................................................... 24
При расположении проводников в одной плоскости.................................... 26
При расположении проводников правильным треугольником.................... 28
1. Основные понятия
Действие электродинамических сил на аппараты
При нормальных эксплуатационных условиях электродинамические силы, как правило, малы и не вызывают каких-либо деформаций, а тем более поломок деталей в аппаратах. Однако при коротких замыканиях эти силы достигают весьма больших значений и могут вызвать деформацию или разрушение не только отдельных деталей, но и всего аппарата. Это обстоятельство требует проведения расчета аппарата (или отдельных его узлов) на электродинамическую устойчивость, т.е. на способность выдержать без повреждений прохождение наибольшего возможного в эксплуатационных условиях (или заданного) тока короткого замыкания. Такой расчет тем более необходим ввиду того, что с целью получения минимальных габаритов в аппаратах стремятся располагать токоведущие части как можно ближе друг к другу.
Так как переменный ток при отсутствии апериодической составляющей отличается от постоянного изменением силы тока и направлением изменяющихся по синусоидальному закону, то и электродинамическая сила будет иметь переменное значение.
Для упрощения рассмотрим электродинамические силы, возникающие в различных частях электрического аппарата при постоянном токе. Далее, оценим их влияние на электрический аппарат в различных ситуациях при трехфазном переменном токе.
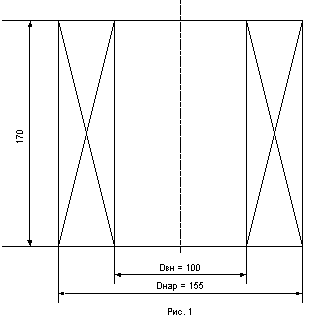
Возникновение электродинамических силОбтекаемый током i прямолинейный проводник длиной l (рис. 1), расположенный в магнитном поле с индукцией В, испытывает механическую силу
![]() (1)
(1)
где β- угол между направлением вектора магнитной индукции и направлением тока в проводнике.
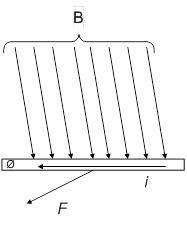
Рис. 1.
Для системы из нескольких обтекаемых током проводников можно всегда представить, что любой из этих проводников расположен в магнитном поле, созданном токами других проводников, и соответствующим образом взаимодействует с этим полем, т. е. между проводниками, охваченными общим магнитным потоком, всегда возникают механические силы. Эти силы называются электродинамическими.
Аналогичные силы возникают между проводником, обтекаемым током, и ферромагнитной массой.
Направление действия силыНаправление действия силы определяется «правилом левой руки».
Направление действия силы может быть также определено из следующего общего положения: силы, действующие в контуре с током, стремятся изменить конфигурацию контура так, чтобы охватываемый контуром магнитный поток увеличился.
Удобным для определения направления действия электродинамической силы является метод, предложенный академиком В.Ф. Миткевичем, основанный на представлении бокового распора и тяжения магнитных линий.
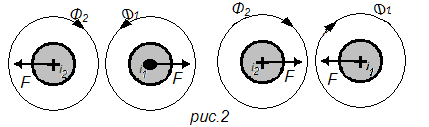
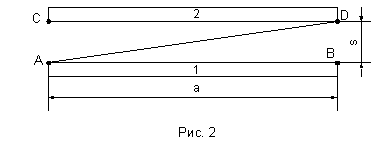
Рисуют и накладывают друг на друга картины магнитных полей, создаваемых током каждого из проводников. Благодаря боковому распору магнитных силовых линий сила, действующая на проводник, направлена в сторону, где поле ослаблено (рис. 2).
2. Методы расчета электродинамических силРасчет электродинамических сил ведется обычно либо на основании закона взаимодействия проводника с током и магнитным полем (первый метод), либо по изменению запаса магнитной энергии системы (второй метод).
Первый метод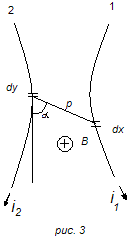
Расчет электродинамических сил на основании закона взаимодействия проводника с током и магнитным полем. Возьмем систему из двух произвольно расположенных проводников 1 и 2 (рис. 3), обтекаемых токами i1 и i2.Напряженность магнитного поля, создаваемого элементом dy проводника 2 в месте расположения элемента dx проводника 1, будет
![]() (2)
(2)
где α — угол между вектором ρ и направлением тока по элементу dy.
Весь проводник 2 создает в месте расположения элемента dx напряженность магнитного поля
![]() (3)
(3)
Элементарная сила, действующая на элемент dx, обтекаемый током i1
![]() (4)
(4)
где ρ — угол между вектором магнитной индукции В = μ0Hdx и вектором тока i1;
μ0— магнитная проницаемость воздуха.
Полную силу F взаимодействия между проводниками 1 и 2 получим после интегрирования dFdx по всей длине проводника 1:
![]() (5)
(5)
Считая токи i1 и i2 неизменными по всей длине проводника, уравнение (5) можно переписать в виде произведения членов:
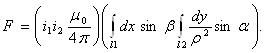 (6)
(6)
Первый член этого выражения зависит только от значений токов. Второй член зависит только от взаимного геометрического расположения проводников и представляет собой безразмерную величину. Эту величину часто называют коэффициентом контура, который обозначим буквой с. Тогда
![]() (7)
(7)
т.е. сила взаимодействия между двумя проводниками, обтекаемыми токами i1 и i2, пропорциональна произведению этих токов (квадрату тока при i1 = i2) и зависит от геометрии проводников.
Подставив в уравнение (7) значение μ0 = 4π10-7 и вычисляя силу в ньютонах, получим
![]() (8)
(8)
Расчет электродинамических сил по изменению запаса электромагнитной энергии контуров. Электромагнитное поле вокруг проводников и контуров с током обладает определенным запасом энергии. Электромагнитная энергия контура, обтекаемого током i,
![]() (9)
(9)
Электромагнитная энергия двух контуров, обтекаемых токами i1 и i2,
![]() (10)
(10)
где L1,L2 — индуктивности контуров; М — взаимная индуктивность контуров.
Всякая деформация контура (изменение расположения отдельных его элементов или частей) или изменение взаиморасположения контуров приводят к изменению запаса электромагнитной энергии. При этом работа сил в любой системе равна изменению запаса энергии этой системы:
![]() (11)
(11)
здесь dW — изменение запаса энергии системы при деформации системы в направлении х под действием силы F.
На указанном законе (11) и основан второй метод определения электродинамических сил в контурах. Электродинамическая сила в контуре или между контурами, действующая в направлении х, равна скорости изменения запаса энергии системы при деформации ее в том же направлении:
![]() (12)
(12)
Согласно сказанному электродинамическая сила в контуре, обтекаемом током i,
![]() (13)
(13)
а электродинамическая сила между двумя взаимосвязанными контурами с токами i1 и i2 будет
![]() (14)
(14)
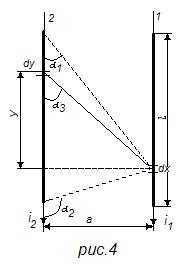
Возьмем два параллельных круглых проводника 1 и 2 (рис. 4), расположенных в одной плоскости на расстоянии друг от друга и обтекаемых токами i1 и i2. Расчет будем производить первым методом. Проделав все операции аналогично выражениям (2) — (8) и учитывая, что sin β = 1, так как проводники расположены в одной плоскости, и вектор индукции в данном случае перпендикулярен этой плоскости (β=90°), получим
![]() , (15)
, (15)
где
![]()
Выразим подынтегральные переменные второго интеграла через одну из переменных, а именно через угол α. Примем за начало координат элемент dy и направление токов, совпадающее с положительным направлением координат. В этом случае текущая координата
![]() (16)
(16)
Подставив полученные выражения в уравнение (15) и считая, что проводник 2 распространяется от — ∞ до + ∞, чему соответствует изменение угла α от π до 0, получим
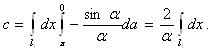 (17)
(17)
Очевидно, если проводник 1 (l1), так же как и проводник 2, распространяется до ±∞, то с будет стремиться к бесконечности.
Конечной длиныЕсли проводник 1 имеет конечную длину, то
![]() (18)
(18)
Согласно выражению (8) сила, действующая на проводник 1, равна
![]() (19)
(19)
Уравнение (19) определяет силу взаимодействия между двумя проводниками, один из которых бесконечно длинен, а второй имеет конечную длину l и расположен симметрично относительно первого. В случае, когда оба проводника будут иметь конечную длину l, пределы интегрирования для выражения (17) будут уже не от π до 0, а от α 2 до α 1 (см. штриховые линии на рис. 4) и сила взаимодействия между двумя круглыми проводниками конечной и равной длины определится уравнением
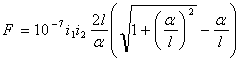 . (20)
. (20)
В уравнении (20) множитель перед скобками представляет собой силу взаимодействия между двумя проводниками, один из которых имеет бесконечную длину. Обозначим эту силу через F∞. Коэффициент, заключенный в скобках, представляет собой величину, меньшую единицы. При α/1<0,2 (в практике, как правило, α/1<< 0,2) величиной (α/l)2 по отношению к единице можно пренебречь. Тогда уравнение (20) примет вид (21)
![]() (21)
(21)
В практике весьма часто проводники имеют неравную длину. Силу взаимодействия между такими проводниками можно найти изложенным выше способом, производя интегрирование каждый раз в соответствующих пределах. Можно эту задачу решить, применив уравнение (20).
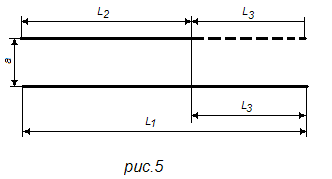
На рис. 5 приведены два проводника неравной длины l1 и l2, расположенные друг от друга на расстоянии а и обтекаемые токами i1 и i2. Нарастим проводник l2 на отрезок l3 до длины, равной l1. Проводник l1 можем также представить состоящим из двух отрезков l2 и l3. Тогда можем написать, что сила взаимодействия между проводниками длиной l1 и l2 (F l1 l2) равна сумме сил взаимодействия между двумя проводниками l2 одинаковой длины (F l2 l2) и двумя проводниками длиной l2 и l3 (F l2 l3):
![]() (22)
(22)
Аналогично можно написать
![]() (23)
(23)
Сложив уравнения (22) и (23), получим
![]() (24)
(24)
Таким образом, сила взаимодействия между двумя проводниками неравной длины выражается через силу взаимодействия проводников равной длины:
![]() (25)
(25)
При этом l1 и l2 — величины заданные, а l3= l1 - l2.
Сила взаимодействия между круглыми параллельными проводниками может быть также определена по изменению запаса электромагнитной энергии.
Первый случай — оба проводника принадлежат к одной системе. Индуктивность системы из двух параллельных проводников радиусом r и длиной l, находящихся на расстоянии а, при условии, что l >> а, определяется формулой
![]() (26)
(26)
Нас интересует сила, действующая в направлении а. Согласно выражению (13)
![]() (27)
(27)
из уравнения (26)
![]()
тогда
![]() (28)
(28)
Из выражения (28) видно, что результат получился таким же, как и при определении этих сил, первым методом.
Второй случай — проводники принадлежат к двум различным системам, при этом сами системы не претерпевают деформации. Взаимная индуктивность между двумя проводниками длиной l, находящимися друг от друга на расстоянии а, при условии, что l >> а, определяется формулой
![]() (29)
(29)
Согласно формуле (13) сила, действующая в направлении а,
![]()
где
![]()
так как сами системы не претерпевают деформации, а из выражения (29)
![]()
Тогда
![]() (30)
(30)
т.е. результат, как и следовало, получился тот же.
Для двух параллельных проводников, расположенных с любым сдвигом, Г.Б. Холявский получил удобную для расчета коэффициента контура формулу, основанную на геометрической интерпретации приведенных выше уравнений.
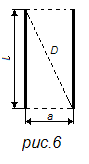
Величина ![]() представляет собой длину диагонали D (рис. 6) прямоугольника со сторонами l и а; следовательно, согласно уравнению (20) для проводников равной длины
представляет собой длину диагонали D (рис. 6) прямоугольника со сторонами l и а; следовательно, согласно уравнению (20) для проводников равной длины
![]() (31a)
(31a)
а согласно уравнению (25) для проводников неравной длины (рис. 7)
![]() (31б)
(31б)
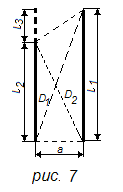
т.е. коэффициент контура равен разности суммарных диагоналей и боковых сторон четырехугольника (прямоугольник, трапеция, параллелограмм), построенного на данных отрезках проводников, деленной на его высоту.
Для проводников прямоугольного сечения (шин) следует вводить поправочный коэффициент — коэффициент формы kф, зависящий от размеров проводников и расстояний между ними:
![]() (32)
(32)
Похожие работы
... контактов обеспечивается выбором их материала и конструкции при использовании одноступенчатой системы. В заключение отметим, что в настоящее время начинают широко применяться электрические аппараты с герметизированными контактами и контактами, работающими в глубоком вакууме. Жидкометаллические контакты? Наиболее характерные недостатки твердометаллических контактов следующие: 1. С ростом ...
и ϑдоп = 90 оС. Коэффициент теплоотдачи . Поскольку должно быть равенство между выделенной в катушке и отводимой с ее поверхности тепловыми мощностями, то исходным уравнением для нахождения допустимой плотности тока будет: , Откуда , где, – площадь поперечного сечения провода; r0 = 1,62 ∙ 10-6 Ом ∙ см; a = 0,0043 1/град; ; – длина среднего витка катушки. ...
... (5.2), где - ударный коэффициент, который составляет (табл.5.1). Расчёт ТКЗ выполняется для наиболее экономичного варианта развития электрической сети (вариантI рис.2.1) с установкой на подстанции 10 двух трансформаторов ТРДН-25000/110. Схема замещения сети для расчёта ТКЗ приведена на рис. 5.1. Синхронные генераторы в схеме представлены сверхпереходными ЭДС и сопротивлением (для блоков 200МВт ...
... фильтров 1 и 2 ступеней. Промывочные сбросные воды ТЭЦ обезвреживаются по схеме нейтрализации в баках-нейтрализаторах /8/. 7.7 Водно-химический режим на ТЭЦ Водно-химический режим тепловых электрических станций должен обеспечивать работу теплосилового оборудования без повреждений и снижения экономичности, вызванных образованием: накипи, отложений на поверхностях нагрева; шлама в котлах, ...






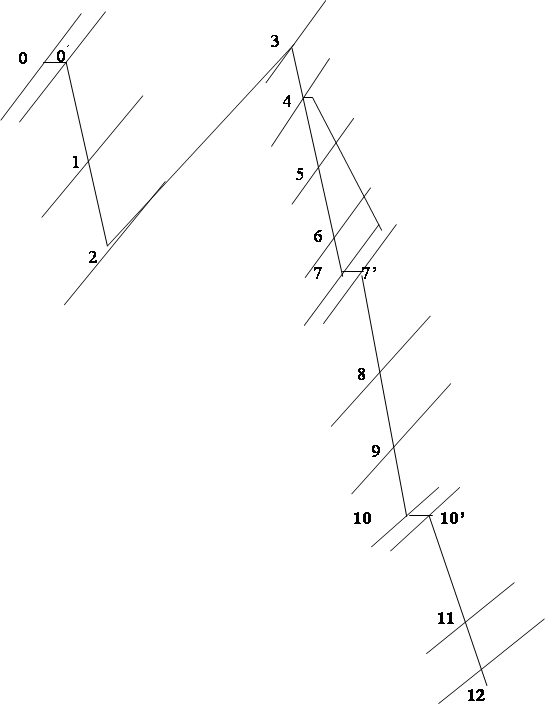
0 комментариев