Электродинамические силы между взаимно перпендикулярными проводниками

4. Электродинамические силы между взаимно перпендикулярными проводниками

На рис. 8 и 9 приведены часто встречающиеся в аппаратах формы перпендикулярно расположенных проводников, например в рубильниках, мостиковых контактных системах и многих других аппаратах и узлах. Произведя расчеты, аналогичные предыдущим (первый метод), получим следующие выражения для сил, действующих на проводник 1 по рис.8
при h →∞

(33)

и при h конечном

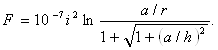(34)

по рис. 9 сила будет соответственно в два раза большей:

(35)

(36)

Моменты относительно точки О, действующие на проводник 1 (h →∞), по рис. 8:

(37)

(38)

Момент относительно точки О, действующий на половину проводника 1 (рис. 9),

(39)

5. Электродинамические силы в кольцевом витке и между кольцевыми витками Для одного витка

В кольцевом витке (рис. 10) с током i возникают радиальные силы f_R, стремящиеся увеличить его периметр, т.е. разорвать виток. Если считать, что сечение проводника не деформируется, то согласно выражению (13) общая радиальная сила, действующая на виток, будет

(40)

На единицу длины витка приходится сила

(41)

Для того чтобы найти силу F_R, стремящуюся разорвать виток, необходимо проинтегрировать проекции радиальных сил, действующих на четверти витка. На элемент окружности витка Rdφ действует сила f_RRdφ, проекция которой на ось х равна f_RRdφ cos φ, откуда

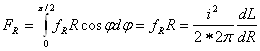(42)

Для витка круглого сечения при R >> r

(43)

и

(44)

Аналогично для витка прямоугольного сечения

(45)

и

(46)

Для нескольких витков

Приведенные формулы для электродинамических сил применимы не только к одному витку, но и к обмоткам с любым числом витков п, занимающим данное сечение. В этом случае за значение тока следует принимать суммарное значение тока всех витков i =ni_в.

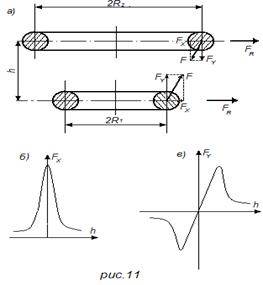
В катушках аппаратов, кроме сил, действующих внутри каждого витка, будут существовать электродинамические силы между витками. Между витками (рис. 11а), если считать, что токи в них направлены одинаково, возникает сила притяжения F. Силу F можно представить как результирующую двух составляющих, а именно силы F_y, стремящейся притянуть витки друг к другу, и силы F_x, стремящейся один из витков (при одинаково направленных токах — виток с меньшим диаметром) растянуть, а другой виток (в данном случае виток большего диаметра) — сжать. Таким образом, в одном из витков сила F_x будет складываться с силой F_R, а в другом — вычитаться из нее.

Значения составляющих силы взаимодействия между двумя витками определяются уравнениями:

(47)

(48)

где c = R₂-R₁; R₂> R₁. Зависимости F_x и F_y от расстояния между витками представлены на рис. 11, б и в.

 

6. Электродинамические силы в проводниках переменного сечения

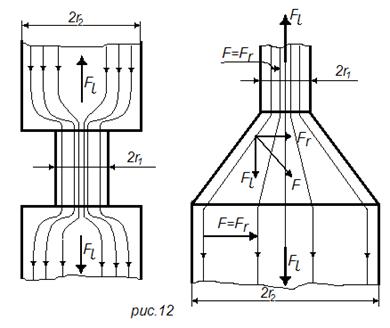
В проводнике силы взаимодействия отдельных линий тока с собственным магнитным полем проводника направлены перпендикулярно линиям тока. При неизменном сечении проводника все линии тока параллельны и силы не имеют осевой составляющей (в цилиндрическом проводнике они направлены по радиусу: F = F_r на рис. 12).

При изменении сечения проводника линии тока искривляются, и кроме поперечной F_rпоявляется продольная составляющая F_l стремящаяся разорвать место перехода вдоль оси проводника. Эта сила всегда направлена в сторону большего сечения и равна

(49)

Формула справедлива для любого перехода.

7. Силы взаимодействия между проводником с током и ферромагнитной массой Вблизи ферромагнитной массы

Вблизи ферромагнитной массы магнитное поле вокруг проводника с током (рис 13) искажается, магнитные силовые линии стремятся замкнуться по массе и возникают силы, стремящиеся притянуть проводник к этой массе.

Значение силы притяжения может быть определено из следующих соображений. Заменим ферромагнитную массу вторым проводником с током того же направления, расположенным на таком же расстоянии от границы раздела сред. Картина поля при этом не нарушится, так как одновременно с удвоением длины магнитной силовой линии удвоилась и магнитодвижущая сила (2i вместо i), т.е. такая замена вполне правомерна. Силы взаимодействия между двумя параллельными проводниками подсчитываются по уравнениям (19) и (20). Только в данном случае вместо расстояния а надо брать 2а, т.е.

(50)

Следует при этом помнить, что приведенные рассуждения полностью справедливы при бесконечно большой проницаемости магнитных силовых линий в ферромагнитной массе по отношению к их проницаемости в воздухе. Фактически с учетом магнитного сопротивления массы и насыщения силы будут несколько меньшими.

Внутри ферромагнитной массы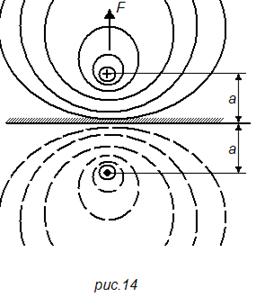

Если проводник с током находится внутри ферромагнитной массы (рис. 14), то те же силы будут отталкивать его от границы раздела. Картина поля, а следовательно, и сила взаимодействия будут такими, как если бы за пределами ферромагнитной массы на таком же расстоянии был расположен проводник с таким же током, но обратного направления. Значение силы определяется тем же уравнением (50).

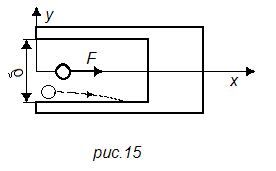
Аналогичные силы притяжения будет испытывать проводник, расположенный в щели постоянного (рис. 15) или переменного (рис. 16) сечения в ферромагнитной массе. Без учета насыщения

(51)

где l - длина щели (перпендикулярно плоскости чертежа); δ и δ_Х — ширина щели в месте расположения проводника.

В щели постоянного сечения сила, затягивающая проводник вглубь, будет неизменной, а в щели переменного сечения — переменной, возрастающей по мере сужения щели.

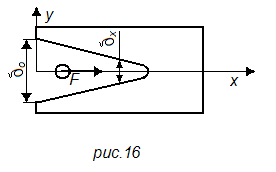
Уравнение (51) относится к проводнику, расположенному в щели строго симметрично, когда сила действует по оси х. Однако если проводник окажется смещенным с оси симметрии, то силы притяжения его к противоположным стенкам (по оси у) окажутся неравными. Проводник будет перемещаться по какой-то кривой, показанной штриховой линией, определяемой двумя переменными составляющими сил F_x и F_y.

8. Электродинамические силы при переменном токе При однофазном токе

Рассмотрим силы, действующие между параллельными проводниками, сначала при однофазном токе.

Согласно выражению (15) электродинамические силы

При переменном токе i = I_msinωt сила

(52)

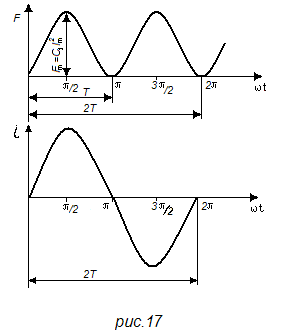
Т.е. сила меняется с частотой, в два раза большей частоты тока (рис. 17).

Силу f можно представить как сумму двух составляющих: постоянной  и переменной , меняющейся с двойной частотой по закону косинуса. Так как косинус угла принимает значения от +1 до -1, то сила будет изменяться от до не меняя своего знака.

В расчетах учитывается максимальное значение силы

(53)

Из уравнения (53) видно, что при переменном однофазном токе максимальное значение электродинамической силы при одном и том же значении тока (действующем) оказывается в два раза большим, чем при постоянном.

При переменном токе следует иметь в виду еще одно весьма важное обстоятельство. В отличие от постоянного тока, при котором максимальное значение тока короткого замыкания равно его установившемуся значению I_уст (если пренебречь изменением сопротивления за счет нагрева), при переменном токе в зависимости от момента короткого замыкания первая амплитуда ударного тока I_удmax может существенно превосходить амплитудное значение установившегося тока короткого замыкания (рис. 18):

(54)

Максимальное усилие, на которое следует в таком случае рассчитывать устройство, будет

(55)

т.е. при равном значении установившегося тока короткого замыкания при переменном токе электродинамическая сила может быть почти в 6,5 раза большей, чем при постоянном токе.

При трехфазной сети токи в фазах будут сдвинуты на 120 электрических градусов:

При расположении проводников в одной плоскости

Рассмотрим случай, когда проводники расположены в одной плоскости (рис. 19). Проводник 1 будет взаимодействовать с проводниками 2 и 3. Пусть сила взаимодействия между проводниками 1 и 2 при единице тока равна F₁₂, а между проводниками 1 и 3 — F₁₃. Токи в фазах равны. Тогда полная сила, действующая на проводник 1, определится выражением

(56)

В отличие от однофазного тока при трехфазном токе сила меняется не только во времени, но и по знаку. При положительных значениях sin2ωt и cos2ωt получим силу, притягивающую проводник 1 к двум другим. При отрицательных значениях sin2ωt и cos2ωt получим силу, отталкивающую проводник 1 от двух других.

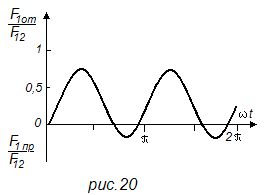
Проводники обычно располагаются на равном расстоянии друг от друга. В таком случае F₁₃ = 0,5F₁₂, и тогда в установившемся режиме (рис. 20) максимальная притягивающая сила

(57)

а максимальная отталкивающая сила

(58)

Силы, действующие на проводник 3, будут такими же, как и силы, действующие на проводник 1, но обратными по направлению.

Усилия, действующие на средний проводник, F₂ определятся уравнениями, аналогичными предыдущим. Если принять силу взаимодействия при единице тока между проводниками 2 и 3 равной F₂₃ а между проводниками 2 и 1-равной F₂₁ = F₁₂ то при равных токах и равных расстояниях между проводниками F₂₃ = F₂₁ = F₁₂ и максимальная сила, действующая на средний проводник, определится из уравнения

(59)

Таким образом, при расположении проводников в одной плоскости сила, действующая на средний проводник, оказывается большей, чем сила, действующая на крайний проводник.

С учетом переходной составляющей, возникающей в момент короткого замыкания, максимальные силы будут большими, чем приведенные выше. Максимальное отталкивающее усилие будет при коротком замыкании в момент φ =-15° и составит

(60)

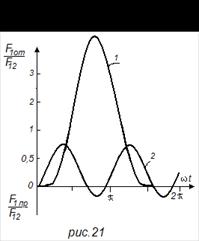
Притягивающая сила при φ =-15° будет близка к нулю. Максимум притягивающей силы имеет место при коротком замыкании в момент φ =75°:

(61)

Значение отталкивающей силы при φ = 75° составит 0,75F₁₂. Изменение сил во времени при φ = -15° (кривая 1) и φ = 75° (кривая 2) в переходном режиме короткого замыкания приведено на рис. 21.

При расположении проводников правильным треугольником

Рассмотрим еще один случай, когда провода трехфазной цепи расположены правильным треугольником. Определим силы, действующие на проводник 1. Сила взаимодействия между проводниками 1 и 2 (F_l2) будет направлена по прямой I, а сила взаимодействия между проводниками 1 и 3 (F₁₃) — по прямой II. Каждая из сил будет переменной во времени, а общая сила (F₁), полученная путем геометрического сложения переменных по значению сил F_l2 и F_l3, будет переменной не только во времени, но и по направлению.

Изменение полученной силы F₁ по направлению и по значению может быть охарактеризовано вектором ОА, конец которого будет скользить по окружности, как это показано на рис. 22:

(62)

Проекция силы на ось х всегда направлена в одну сторону. Знак ± в уравнении (62) означает, что для 2ωt>180° следует брать знак минус. Изменение силы во времени не связано с изменением знака.

Каждый из двух других проводников испытывает такие же силы, но с соответствующим сдвигом во времени и пространстве.

С учетом ударного тока максимум силы получается при условии φ = 0, и сила меняется по закону

(63)

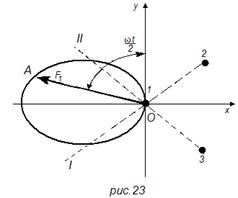
Знак минус следует брать для всех отрицательных значений sin ωt/2. Направление и значение силы для любого момента времени определяется вектором ОА, скользящим по кривой (рис. 23) и отложенным под углом ωt/2 к оси ординат.

В трехфазной сети могут быть однофазные, двухфазные и трехфазные короткие замыкания, но так как токоведущие части должны противостоять электродинамическим силам при любом виде короткого замыкания, то, следовательно, расчет надо вести на тот вид короткого замыкания, при котором силы получаются большими.

При двухфазном коротком замыкании электродинамические силы получаются большими, чем при трехфазном, если предположить, что ударный ток в обоих случаях одинаков. Практически ударный ток при двухфазном коротком замыкании меньше, чем при трехфазном. Поэтому расчет токов короткого замыкания рекомендуется вести всегда на случай трехфазного короткого замыкания.

Расчет ведется на максимальное усилие, получаемое при ударном токе. Однако, учитывая, что сила переменна и ее максимум существует очень короткое время, для допустимых напряжений в материале берут большие значения, чем при постоянно действующей силе.