Режим поиска принимаемых сигналов

2.4 Режим поиска принимаемых сигналов

Измерительные следящие системы за временным положением (задержкой) огибающей (ССЗ) и за фазой несущей (ССН) могут функционировать после завершения операций поиска псевдослучайного сигнала (т.е. после грубого совмещения принятого  и опорного  кодов).. Необходимо детально изучить и воспроизвести схему поиска рис.13.2 [1], дополнив указанием, что опорное напряжение на входе нижнего ФД имеет вид . Задаваясь  и С=+1, следует построить примерный график зависимости видеонапряжения на выходе верхнего фильтра ФНЧ от интервала между начальными метками периодов сигнального и опорного кодов. Необходимо добиться четкого понимания (и уметь объяснить) почему этот график должен соответствовать функциям корреляции, определяемым по формулам на с.288 [1].

2.5 Режим автоподстройки частоты (АПЧ)

После режима поиска до функционирования ССЗ и ССН работает схема АПЧ в соответствии со схемой рис.13.4[1], которую необходимо изучить. Доказать, что на ГУН несущей воздействует управляющий сигнал, указанный на схеме.

3. Режим определения координат и времени

3.1 Модель и погрешности измерения временного положения огибающей

Измеритель временного положения огибающей.

Схема рис.13.7 [1] дополняется двумя блоками: бортовым хранителем времени (БХВ), метки электронной шкалы времени которого служат опорными для измерителя временных интервалов (ИВИ). На второй вход ИВИ подаются метки начала периода с ГУН кода , который управляется на рис.13.7[1] напряжением, пропорциональным  до тех пор, пока величина  не будет близка нулю. Необходимо детально изучить и знать процессы в схеме рис.13.7[1] и иллюстрировать их временными диаграммами, подобными рис. 13.6 [1].

Если БХВ имеет уход шкалы времени , то ИВИ (при отсутствии других погрешностей) позволяет получить квазидальномерные отсчеты в единицах времени . С последующим (в п.3.2.1) переходом к линейным единицам.

Шумовая погрешность

Методика оценки средней квадратической шумовой погрешности слежения за временным положением огибающей дана на с.32-45 [1]. Для расчетов удобна формула из параграфа 42 [4], выражающая сразу погрешность оценки квазидальности по ССЗ в метрах

=745.22065894

Расчет следует выполнить при .

Другие источники погрешностей в ССРНС "ГЛОНАСС" по ССЗ (с.300 [4]):

- неточность прогноза координат и ухода шкалы времени - 4 м;

- возмущение орбит и немоделируемые уходы шкалы времени - 3 м;

- неточность прогноза времени распространения в тропосфере - 2 м;

- неточность прогноза времени распространения в ионосфере - 9 м;

- многолучевость распространения - 1,2 м;

- прочие источники - 1 м.

Результирующая погрешность находится как квадратный корень из суммы квадратов составляющих п. 3.1.2 и п. 3.1.3.

σrez’=11.622350668

В дифференциальных подсистемах ССРНС, за счет использования информации с контрольно-корректирующих пунктов исключается первая и четвертая из перечисленных в п. 3.1.3 составляющих.

Рекомендуется продумать как определить погрешность  в значении средней концентрации N электронов в ионосфере вызывает указанную в п.3.1.3 четвертую (наиболее значимую) составляющая Dr=9м. Для этого необходимо воспользоваться приведенными на с.257 [1] соотношениями, из которых вытекает:

,

где , .

=0,253186813*1012

3.2 Алгоритм определения координат и поправки к шкале времени

Результаты измерений п.3.1.1 после умножения на скорость распространения радиоволн можно записать в виде:

,

где

,

Оценки искомых X, Y, Z, d могут быть найдены из системы нелинейных уравнений

,

k = 1, 2, 3, 4. Для упрощения расчетов в современной аппаратуре эта система линеаризуется за счет того, что истинные расстояния rпк при малых значениях X, Y, Z незначительно отличаются от счислимых: расстояний (от счислимой точки до ИСЗ) . При этом используется лишь линейная часть разложение величины rпк в ряд Тейлора. Учитывая, что частные производные от  по координатам судна равны (с обратным знаком) направляющим косинусам, значения которых имеются в табл.1, получим линейное приближение:

.

Обозначая разность между счислимым и измеренным расстояниями до ИСЗ через

можно исходную нелинейную систему переписать в виде линейной системы уравнений:

и в матричном виде

.

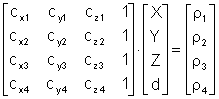=382.102162131

=-1.264662138*10^3

=984.859730108

=50

Детерминант следующей матрицы: =0.441912386

Детерминант матрицы Х: X=574.486101176

Детерминант матрицы Y: Y=574.486101176

Детерминант матрицы Z: Z=22.095619276

Детерминант матрицы D:D=-1.144799074*10^-13=-0.0000000000001144799

Решение этих уравнений через главный  и частные , ,  определители представим в виде линейной комбинации результатов измерений на коэффициенты , , ,  равные отношению соответствующих алгебраических дополнений к :

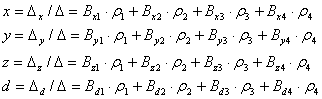
X==1300

Y==1300

Z==50

D==-2.59055665844*10^-13

где, например,

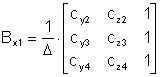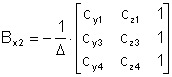; ; ... и т. д..

Каждый исполнитель работы выполняет аналитические выкладки для получения выражений  и B с использованием формулы п.1.4.1

, ,.

Необходимо доказать, что: главный определитель системы уравнений

,

и из шестнадцати коэффициентов В три равны нулю, а остальные равны одному из всего семи значений, так что:

При расчете данных выражений использовались значения Н: Н1=Н2=Н3=43; Н4=90

Аналитические выкладки следует привести в приложении к отчету. При защите работы необходимо будет вывести выражение для одного из коэффициентов. Рассчитанные значения коэффициентов поместить в табл.3 с тремя знаками после запятой.