Режим определения истинного курса, крена, дифферента

5. Режим определения истинного курса, крена, дифферента

5.1 Основные понятия пространственной угловой ориентации судна

Ориентация судна это ориентация судовой системы координат относительно неподвижной (пусть – горизонтной) системы координат x,y,z с базисными ортами xо, yо, zо. Вектора (и орты) обозначаются жирным курсивом. Судовая ортогональная система координат фиксируется на каждом судне в процессе строительства и сдаточных испытаний, причем горизонтальная, продольная и поперечная плоскости пересекаются по поперечной, продольной и вертикальной осям. Начальная точка отсчета – точка пересечения осей. Ось абсцисс хП с ортом a и ось ординат уП с ортом b совпадают соответственно с по перечной и продольной осями судна. Орт оси аппликат zП равен a´b и перпендикулярен ортам a и b.

Проекции любого орта е на оси x,y,z координат равны их направляющим косинусам НК (углов между ортом и осями): Прхе=сх, Пруе=су, Прzе=сz. Если проекции этого орта отложить от начала координат и построить прямоугольный параллелепипед, то исходящая из начала координат диагональ такого параллелепипеда и представляет рассматриваемый орт е=x0cx+y0сy+z0cz причем сх2+су2+сz2=1. Это равенство указывает, что вся информация о пространственной угловой ориентации орта любой оси содержится в трех НК. А полная информация об ориентации судна (т.е. о трех осях подвижной системы координат) содержится в матрице из девяти НК; причем равенство нулю скалярных произведений ортов(см./13/,п.14.10-1b) позволяет всегда указать на три НК, через которые выражают и остальные шесть.

Орты продольной и поперечной осей судна далее будут представляться как

b=x0cbx+y0 сby+z0cbz, a=x0cax + y0 cay + z0c az , ( 5.1 )

позволяя дать четкие количественные формулировки для указанных в п.1.4.5. трех параметров угловой ориентации судна:

дифферент Д это угол между ортом b продольной оси уП судна и плоскостью х0у,

2) крен К – угол между ортом а поперечной оси хП и плоскостью х0у,

3) истинный курс И это угол между направленной на север осью ординат у и проекцией орта b продольной оси уП судна на плоскость х0у.

Из прямоугольного параллелепипеда, соответствующего первому равенству (5.1) вытекают компактные соотношения для НК орта продольной оси

cbх=Прxb=cosДsinИ, сby=Пруb =cosДcosИ, сbz=Прzb =sinД.

Лишь один НК орта а выражается компактно: саz=cos(90о-К)=sinК. Далее ограничимся использованием полученных выше компактных выражений четырех НК: они достаточны для определения используемых угловых параметров

И=arctg(сbх/сby), Д=arcsinсbz, К=arcsinсаz . ( 5.2 )

Следует иметь ввиду, что обсуждаемые выше параметры относятся к одномоментному состоянию судна (относящемуся к одному моменту времени) без какой либо привязки с «предисторией» или прогнозом динамического процесса изменения ориентации судна во времени. На практике могут использоваться и другие методы и параметры описания угловой ориентации.

5.2 Алгоритмы и погрешности определения истинного курса, крена и дифферента по сигналам 4-х ИСЗ

Ограничимся рассмотрением случая 4-х ИСЗ, когда k=1.2.3.4 и систему линейных уравнений (5.2) можно представить с помощью апробированных в разделах .3 и 4 матриц

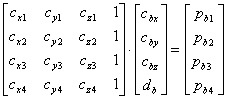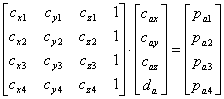; . ( 5.3 )

Необходимые нам направляющие косинусы определяются по формулам раздела.3 (с соответствующей заменой обозначений) .

,

,

,

,

Средние квадратические погрешности определения направляющих косинусов при одинаковых СКП sp величин pak и pbk нормированных разностей расстояний выражаются аналогично (3.6):

; ( 5.4 )

. ( 5.5 )

. ( 5.6 )

Связь погрешности истинного курса DИ, дифферента DД и крена DК (в радианах) с погрешностями направляющих косинусов вытекает, если взять дифференциал соответствующего равенства из (5.1) или (5.2) и заменить знак дифференциала на приращение. Получаем:

DК=Dсaz/cosK, DД=Dcbz/cosД.

Такая же взаимосвязь сохранится и для среднеквадратических погрешностей СКО, т.е.

sК=scaz/cosK, sД=sсbz/cosД,

что с учетом (5.4) позволяет получить расчетные соотношения

sК=spГz/cosK=0.82505, sД=spГz/cosД=0.80505 ( 5.7)

Формулу для оценки погрешностей истинного курса получим, приведя дифференциал истинного курса И=arctg(сbх/сby) к приближению DИ @ сbyDсbх-сbxDсby. Поэтому СКО погрешности с учетом (5.5), (5.6) и (3.7) можно выразить как

sИ=spГм=0.1418 град, где Гм=(Гх2+Гу2)½ (5.8 )

Количественные расчеты погрешностей выполняются для величин, определяемых предыдущими тремя формулами.