Навигация
Оценка влияния погрешностей измерений на определение x, y, z
3.3 Оценка влияния погрешностей измерений на определение x, y, z
Понятие геометрического фактора (см. с.83 /1/) облегчает оценку точности системы в предположении одинаковости дисперсий ![]() и некоррелированности результатов измерений. Эти требования удовлетворяются из-за одинаковости условий приема сигналов различных ИСЗ.
и некоррелированности результатов измерений. Эти требования удовлетворяются из-за одинаковости условий приема сигналов различных ИСЗ.
При некоррелированности погрешностей измерений и одинаковости дисперсий (![]() ) применимо известное из теории вероятностей правило (см. с.326-327 [1]): дисперсия линейной комбинации равна произведению дисперсии
) применимо известное из теории вероятностей правило (см. с.326-327 [1]): дисперсия линейной комбинации равна произведению дисперсии ![]() на сумму квадратов коэффициентов. Применительно к решениям системы п.3.2.1 - это правило дает равенства:
на сумму квадратов коэффициентов. Применительно к решениям системы п.3.2.1 - это правило дает равенства:
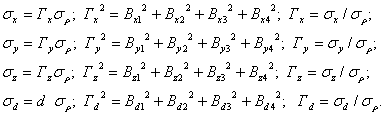
Величина Г и называется геометрическим фактором, зависящим лишь от взаимного геометрического расположения ИСЗ и судна.
Рассчитать геометрические факторы с двумя знаками после запятой
(![]() 1.11,
1.11, ![]() 1.11,
1.11, ![]() 1.81,
1.81, ![]() ).
).
Рассчитать геометрический фактор погрешности местоопределения на поверхности Земли ![]() и в пространстве
и в пространстве ![]() :
:
![]() =2.406039961,
=2.406039961, ![]() =1.578853755.
=1.578853755.
Рассчитывается погрешность местоопределения судна (на поверхности) в среднеорбитальной спутниковой РНС и по дифференциальной подсистеме - с учетом результатов п.3.1.3 - 3.1.4.
Данные расчета занести в табл.1.
Таблица 1
| Система | ССРНС | Навстар | Диф. ССРНС |
| sм (м) | 18,32 | 50,08 | 10,93 |
4. Режим определения путевой скорости, путевого угла и поправки к частоте опорного генератора
4.1 Модель фазового измерителя секундных приращений дальности до ИСЗ
Такой измеритель включает два верхних квадратурных канала рис.13.7 [1] и ГУН несущей, который состоит из высокостабильного неуправляемого опорного генератора ОГ и цифрового синтезатора частоты ЦСЧ, управляемого выходным сигналом схемы Костаса. ЦСЧ содержит регистр текущей разности фаз между колебаниями ОГ и принятого сигнала. Одному фазовому циклу соответствует равное длине волны приращение радиального расстояния от судна до ИСЗ. Из-за принципиальной многозначности фазовых измерений отсчет ЦСЧ в начальный момент времени t0 может отличаться от истинной величины измерявшегося в п.3.2.1 расстояния на неизвестное целое число длин волн. Поскольку это число сохранится во всех последующих отсчетах, то секундные изменения радиального расстояния, (как и приращения ![]() введенных в п.3.2.1 нормированных величин
введенных в п.3.2.1 нормированных величин ![]() ) будут определяться однозначно. Это позволяет по системе четырех линейных уравнений п.3.2.1 однозначно рассчитать и секундные приращения
) будут определяться однозначно. Это позволяет по системе четырех линейных уравнений п.3.2.1 однозначно рассчитать и секундные приращения![]() ,
, ![]() ,
, ![]() ,
, ![]() входящих в это уравнения X, Y, Z, d.
входящих в это уравнения X, Y, Z, d.
4.2 Определение секундных приращений координат
Они численно равны соответствующим проекциям вектора путевой скорости. А секундное приращение линейного эквивалента ухода шкалы времени в длинах волн равно разности между номиналами частот опорных генераторов ИСЗ и судна. Поэтому алгоритм определения перечисленных искомых величин сводится (после изменения обозначений по правилу: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ) к решению системы линейных уравнений п.3.1 в виде
) к решению системы линейных уравнений п.3.1 в виде
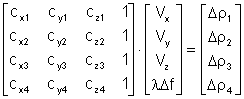 .
.
Все полученные выше в п.3 аналитические выражения и численные значения для решения системы и геометрических факторов применимы и здесь с учетом изменения обозначений. В частности, погрешность оценки горизонтальной проекции
![]()
вектора путевой скорости и ухода частоты должны выражаться как
![]() ,
, ![]() .
.
Среднеквадратическая шумовая погрешность определения секундных приращений дальности ![]() в
в ![]() больше погрешности фазовых квазидальномерных отсчетов и выражается формулой
больше погрешности фазовых квазидальномерных отсчетов и выражается формулой
sDr »0,043[ПССН(N0/Р)]0,5 =0.152 (в м/с). (4.3)
Пссн=10
No/P=0.00007403 см.п. 2.3
Результаты расчетов, задаваясь П=10Гц, привести в таблице 2.
Таблица 2.
| Величина |
|
|
| |
| Значение | 0,00116 | 0,1023520 | 0.000058697 | |
При расчете использовались значения ![]() см.п.2.1,
см.п.2.1,
Vx= 7.583626043 м/с; Vy= 8.511675278 м/с; см. п. 1.4.5
Путевой угол ПУ=arctg(Vx/Vy)- это угол между проекцией Vxy вектора V на горизонтальную плоскость Погрешность оценки путевого угла приближенно выражается формулой
![]() .
.
0 комментариев